「随笔小记」大模型随笔
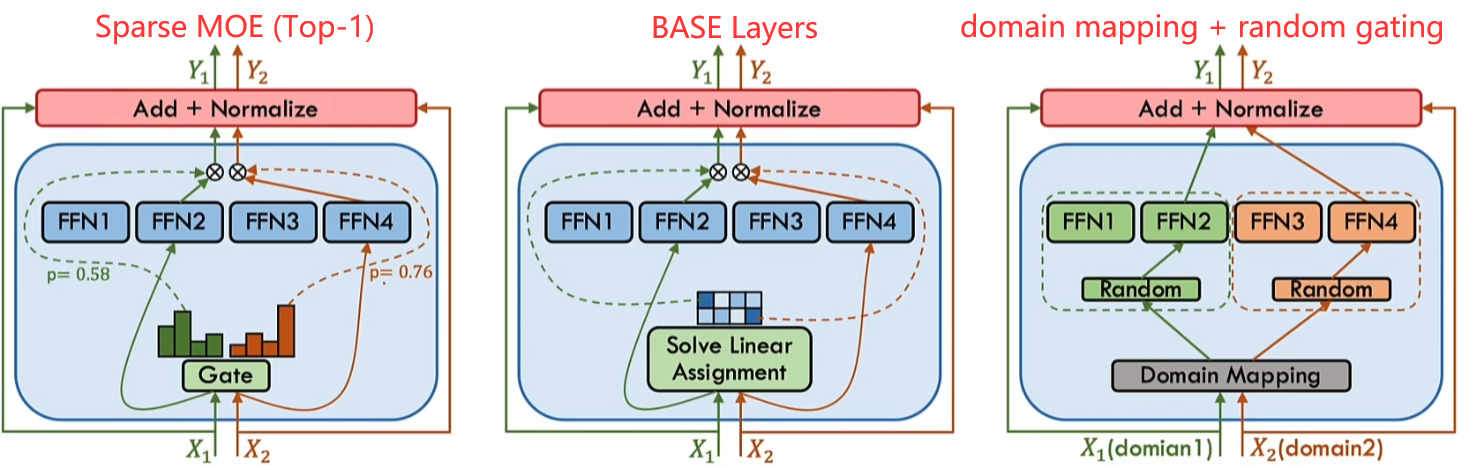
MOE基本类型
MOE全称Mixtrue of Experts (混合专家)
简单来说,就是使用MOE替换Transformer之前的FFN(前馈网络)结构,从而获取更多的信息。
Transformer直接的堆叠,在层数深了之后会导致提取特征的低秩现象。添加残差和前馈神经网络(FFN)可以避免这种现象。
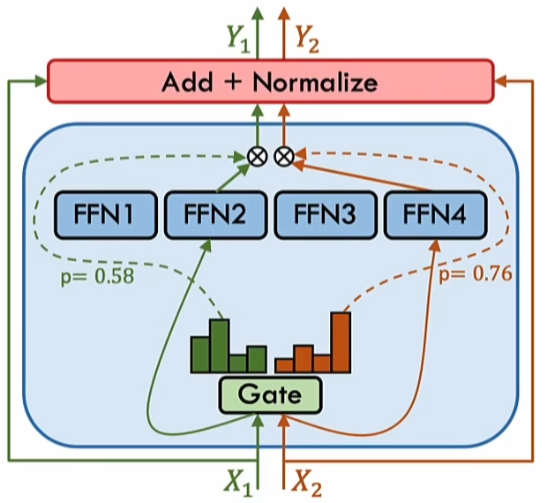
MOE的基本结构如下图:
这里的就是不同的4个专家
对于输入,首先会通过一个门控网络决定走哪一个FFN,然后将计算结果与对应的门控权重进行乘积,将结果与输入进行残差连接和归一化,最后输出结果。
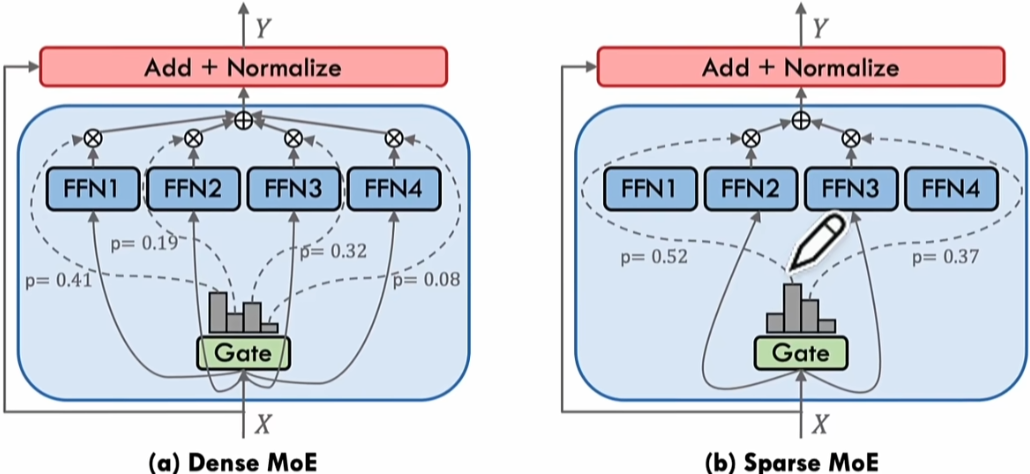
稀疏MOE与稠密MOE
-
门控函数(路由函数):协调专家与其各自输出组合
-
门控函数的分类
-
稀疏门控:激活部分专家
-
稠密门控:激活所有专家
-
软门控:输入Token合并和专家合并
-
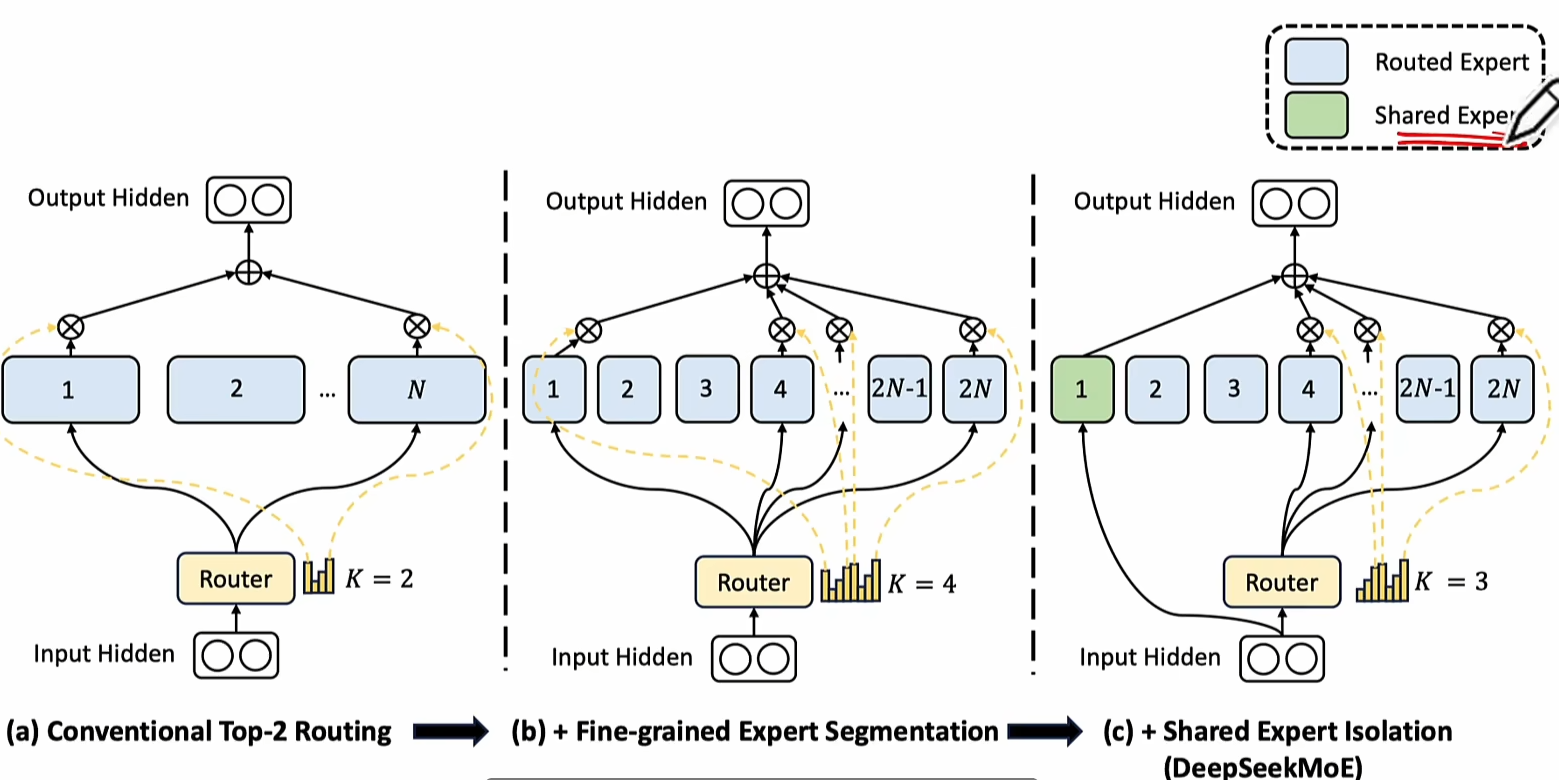
DeepSeek MOE
- Expert共享机制:部分Expert在不同Token或层间共享参数,减少模型冗余。
- Expert共享多了一个Expert作为Shared Expert,每个Expert的计算都使用它
- 内存优化:MLA+KV Cache优化,减少生成任务中的浮点运算量
DeepSeek V2
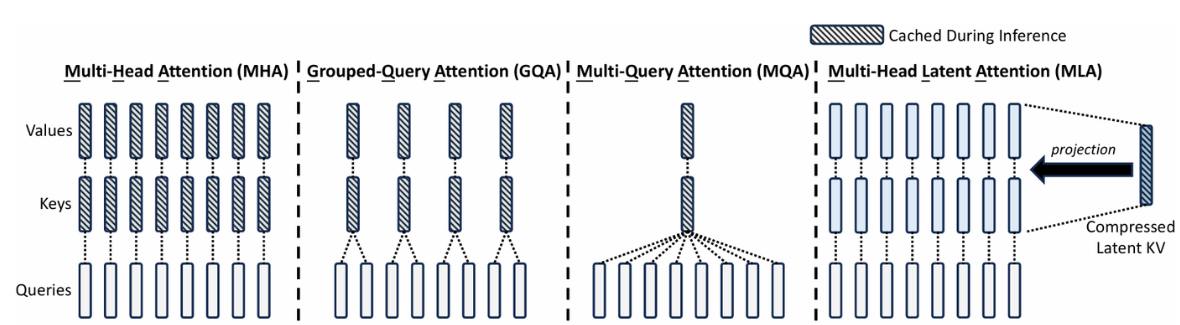
MLA
multi-head latent attention 利用了一套低秩联合压缩的架构节省了很多KVcache的显存
对比算法MQA(multi-query attention),GQA(Grouped-Query Attention),MHA(multi-head Attention)
MQA:所有的Q共用一个KV
GQA:对Q进行分组,相同组内共用KV
MHA:对每个Q都使用不同的KV
基本思路
对于输入,按照self-attention的思路,他会将其映射成Q,K,V三个embedding,这里在映射之前,提前利用低秩联合压缩将压缩成和,首先看Q的生成,使用乘一个Q权重,然后生成,另一个是在这基础之上应用RoPE位置编码,最后将两个部分拼接起来合成最终的Q。接着看KV的部分,乘上对应的K权重和V权重,生成和两个向量,其中就是最终的V向量,而最终的K向量还需要使用计算RoPE得到最后将和拼接得到最终的K向量。最后把Q,K,V输入到MHA中,完成MLA的计算。
图中有颜色的圈表示在实际推理过程中,会进行缓存的部分,对比于传统的MHA,大大降低了KV Cache
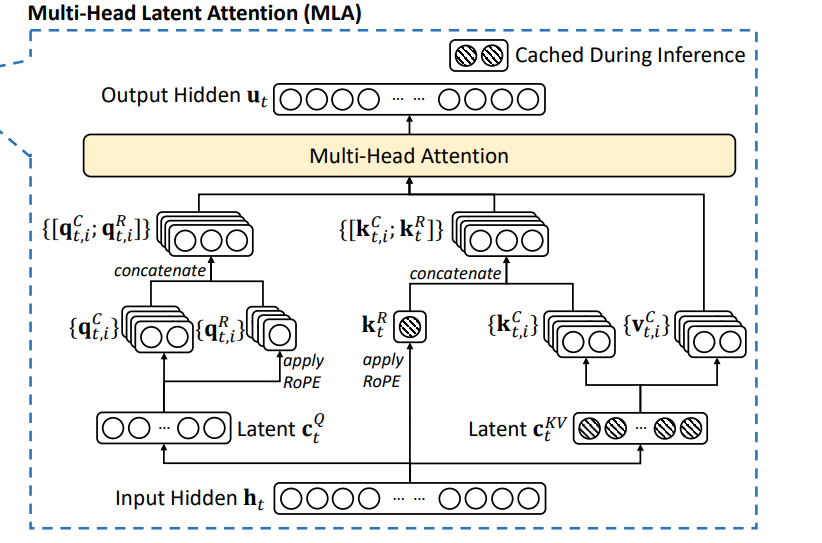
用公式表示如下:(含有D的权重表示低秩压缩(大小降低),含有U的权重表示还原(大小变大)),相比于MHA,就多了和
Flash Attention
参考 [Attention优化][2w字]🔥原理篇: 从Online-Softmax到FlashAttention V1/V2/V3 - 知乎 (zhihu.com)
Online-Softmax
save-softmax
3-pass softmax
- 先算最大值:
- 再算求和:
- 最后算每个元素的值:
2-pass online-softmax
合并1-2步
是刚好满足3-pass的第二步
这样只用存储上一步的最小值和上一步的结果就可以计算当前这一步了,规避了计算全局max
Self-Attention
Standard self-Attention
,后续默认
多阶段计算
Multi-pass Self-Attention
利用2-pass online-softmax的基础上添加QKV计算
-
计算QK
-
计算结果
可以变化为
1-pass FlashAttention v1(核心)
令
当时,刚好和multi-pass self-attention的第二步相同
同样的,可以推导出与的关系
这样就可以看到只依赖于上一次的与本次的,可以在一个循环中全部计算完成,就不用两阶段了
所以得到1-pass的计算为
上面的伪代码是按列进行计算的,外层循环是要遍历列的。当然这个步骤可以进行分块计算(tiling)这样可以减少外层循环的次数,还可以增强数据的访问效率。
这里取K时多取了几列,计算时先计算每一个分块每一行的最大值,最后是后面加的部分修改成了对当前块所有列的求和
相比于Standard Self-Attention的计算流程节省了S和P矩阵的显存,减少Q,K的HBM IO
FlashAttention V1原论文对于的求解如下:
看着和之前推导的公式差距有点大,那转化一下,上面的其实指的是实际内存空间的地址,而之前写的和中的,表示的是不同迭代次数,和其实也是相同的内存空间地址,这里先带入成之前的符号,这里的其实是和之前推导公式的计算方式不同,他这里是先用局部最大值计算了每个元素的,而上面推导的公式是在最后直接使用全局的最大值进行计算(第一步),然后这里的是将一个一维数组转化成一个对角矩阵的方式,因为每次的计算其实都是只算了一个数据,为了方便理解,可以想象成只有一个元素然后进行转换(第二步)。最后就是将两个的指数进行合并,得到之前推导公式相同的结果(第三步)。
block size的设置
是SRAM的大小,也是L1 cache的大小,通过这样的计算方式,控制Q,O,K,V的大小不会超过SRAM的大小,实现高效的访存。
下面可以推断出通过这样设置和确保Q,O,K,V的中间变量大小都不会超过。
当然这里也会有一些剩余的部分,其实就是给和预留使用,基本上都可以把SRAM打满了
稀疏矩阵的拓展
简单来说就是在原本的基础上,检测每次分块的稀疏度,如果稀疏度为0就跳过对这个小块的计算
反向计算
反向最重要的技术就是recompute,前向计算中省略了中间结果S和P,但是反向需要用他们计算梯度值。
所以反向计算时也会进行tiling,将Q,K,V分块加载到SRAM,再通过recompute的方式计算出当前块的S和P的值,用于求取梯度。
无论是否有recompute,都要去load对应的数据到SRAM中,如果不用recompute就要从HBM中拉取(load Q,K,V,dO,dS, )+ (load P,dP) +(write dS, dP, dQ, dV, dK)
但使用了tiling+recompute之后,只用从HBM拉取(load Q,K,V,dO) + (write dQ,dV,dK),节省了dS,dP,P的IO,虽然recompute技术增加了计算量,但计算过程都是在SRAM中进行的,对比与从HBM拉取数据到SRAM中速度能快很多。
FlashAttention V2
主要优化:
- 减少大量非matmul的冗余计算,增加Tensor Cores运算比例
- forward pass/backward pass均增加seqlen维度的并行,forward pass交替Q,K,V循环顺序
- 更好的Warp Partitioning策略,避免Split-K
减少非matmul的冗余计算
为啥要减少非matmul?因为matmul有专门的硬件(tensor core),可以算得更快。
哪里能减少matmul?就是V1中每一轮迭代都进行了rescale(就是softmax中的分母部分),这东西在V1版本中每一轮都用了,但其实可以在QKV都算完之后再除以的
FA2的计算过程如下:
对比与FA1,计算区别在于那几个的计算,在FA1中每一轮的计算都为,多了的计算步骤
反向计算不再保存和,而是保存
从而减少重计算的计算量。FA1→FA
增加seqlen维度的并行
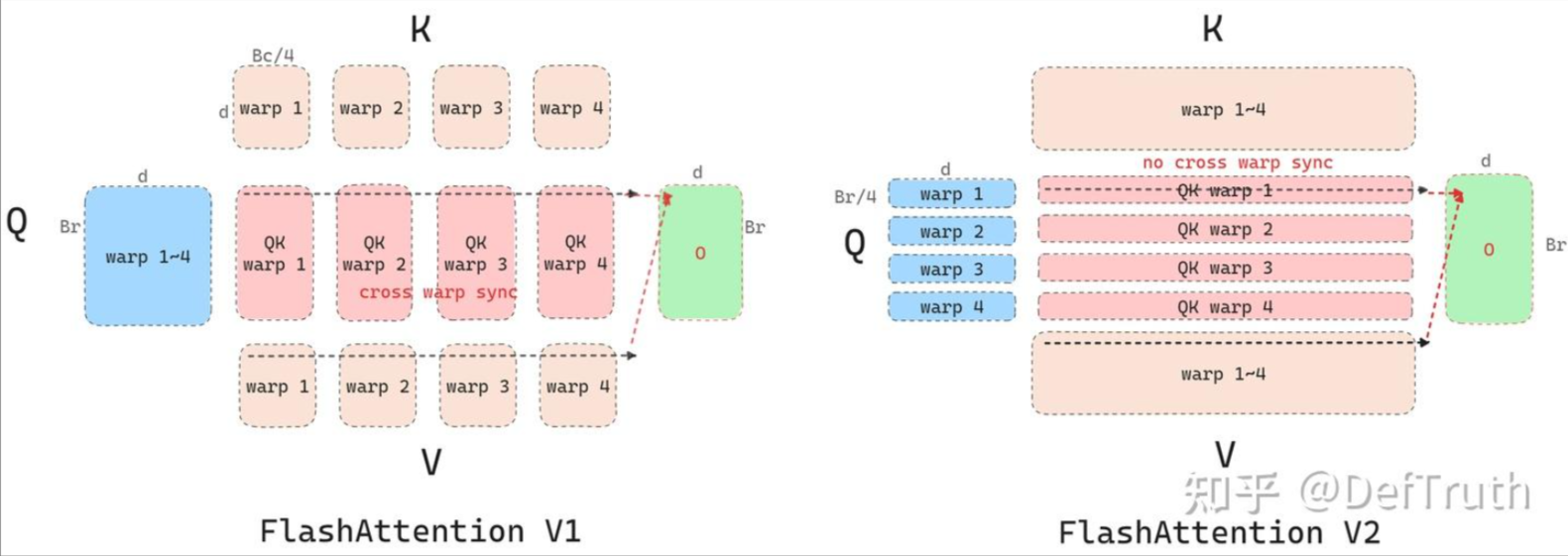
在FA1中,是先load K,V子块,再load Q子块,这使得内循环每轮迭代都只是计算了Q的子结果,想要计算完所有的Q的每一行则是需要整个计算过程结束,此外每一次内循环,都要将结果写入到全局内存中,访问开销很大。
在FA2中,是先load Q子块,再load K,V字块,这使得只要内循环结束,Q的一部分行就能计算完成,而不只是Q的子结果。如果我们在外循环中使用一个本地内存去存储O,然后内循环计算的结果全部写入本地内存中,内循环结束后再写入全局内存,阁下又该如何应对?这种方式是对的,这样每个Q行就可以并行起来了,独立去计算这一行Q的结果,每一行Q都会在内循环结束后得到完整的结果,此外每次内循环访问的都是本地内存,访存开销也大大减少。
反观FA1,只在batch_size和headnum做并行

反向中使用的仍然是先load K,V再load O, 为啥呢,因为每个KV都参与了O的计算,因此要得到dK和dV则需要考虑所有的O

warp partition
FA1可以看做一种split-k的计算,FA2可以看做splitQ的计算,那这两个计算的差异有什么区别呢?
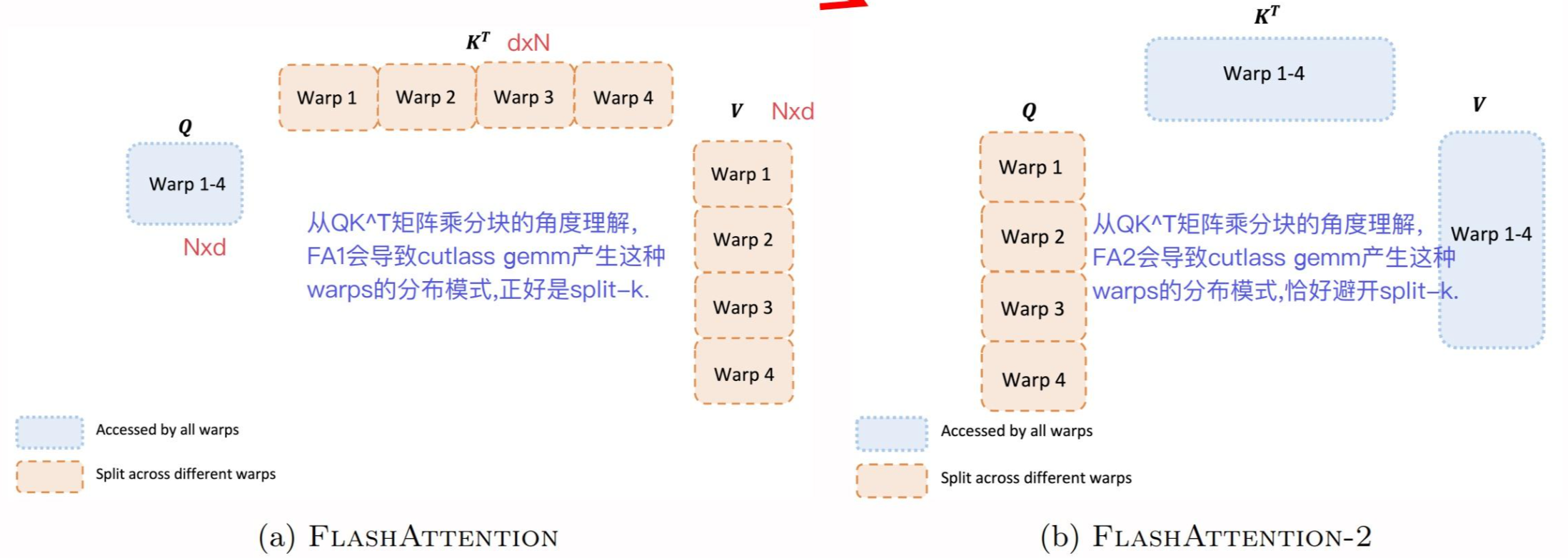
这里看到split-K的做法,会导致在计算QKV时需要跨warp同步通信才能得到最终的结果O,而split-Q的做法,则直接在warp内进行访存计算,消除了通信开销
causal mask的处理
causal mask就是在attention计算结果上乘以一个下三角为1上三角为0的矩阵,这时候flash attention计算过程可以包含这一步骤。
他有三种情况
- FA的子块对应的causal mask全为0,那这个FA的子块就可以不计算了,因为就是0
- FA的子块对应的causal mask全为1,那这个FA的子块计算完成后,可以不与causal mask相乘,因为就是原值
- 比较麻烦的就是FA的子块在全局网格的对角线上,这样的子块对应的casual mask一半是1,一半是0,需要在最后计算结果中乘以causal mask
但如果子块不是矩阵又该如何处理,这里引入一个右对齐的概念,看下图吧:
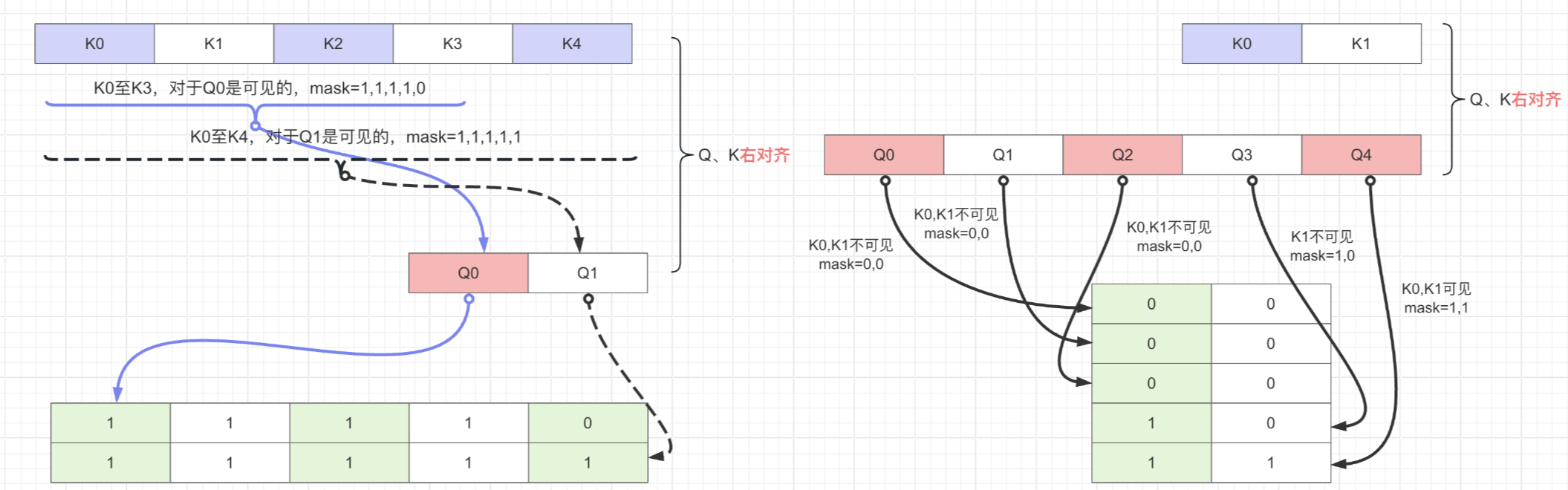
FlashAttention V3
生产者消费者异步化
- warp specialized:warp特化,给不同的warp group角色设置了任务(异步执行)
- producer warp group:负责TMA从全局内存到共享内存的数据加载
- consumer warp group: 负责在共享内存和寄存器中做matmul+softmax+matmul
GEMM和softmax的overlap
将exp指令与tensorcore的WGMMA指令重叠
- inter warpgroup:从warpgourp level出发,通过tileScheduler和barrier的同步控制,使得warpgroup1和warpgroup2可以无缝衔接计算同一个gemm上面的不同output tile,使得tensor core wgmma busy。
- intra warpgroup:
- gemm1依赖softamx,softmax依赖gemm0

支持FP8 FlashAttention
- block quantize: 将权重weight和activation的weight,按照128*128的blocks进行sacle计算(也就是按照128*128的size进行量化)
- gemm0的输出(S)经softmax后不能直接作为gemm1的输入(P矩阵): 数据不连续
- V transpose: QK^T得到[seq_len,seq_len]的矩阵,V是[seq_len, head_dim],但V在head_dim上连续,存在非连续访问。
- Python预处理
- pre-hopper,LDSM_T,在V从sharedmemory加载到register的同时做转置
- hopper,用LDSM_T的source layout拷贝到STSM_N的destination layout,完成转置
FlashDecoding
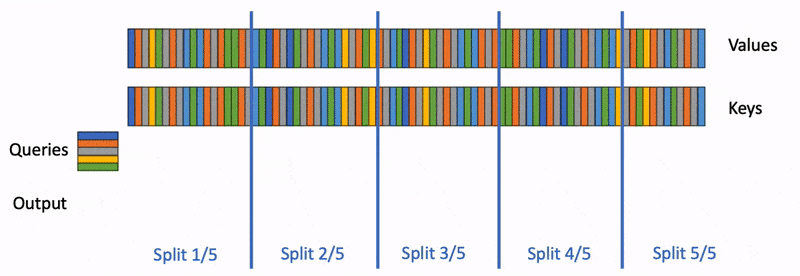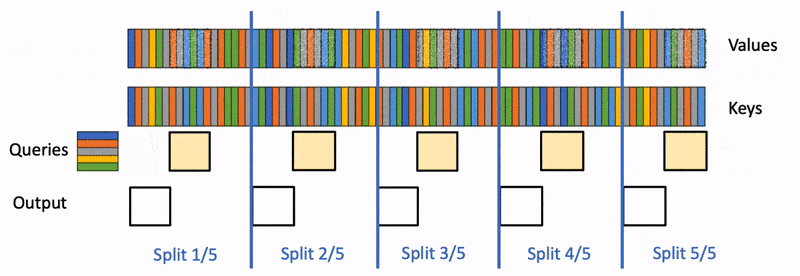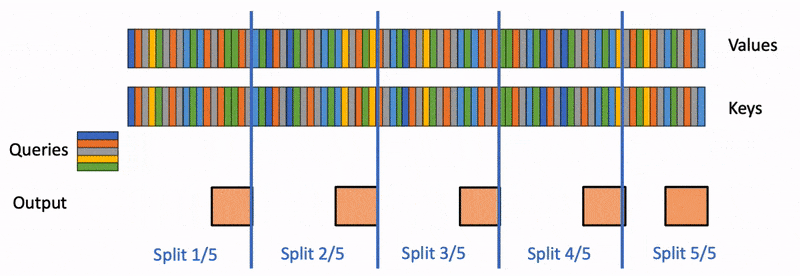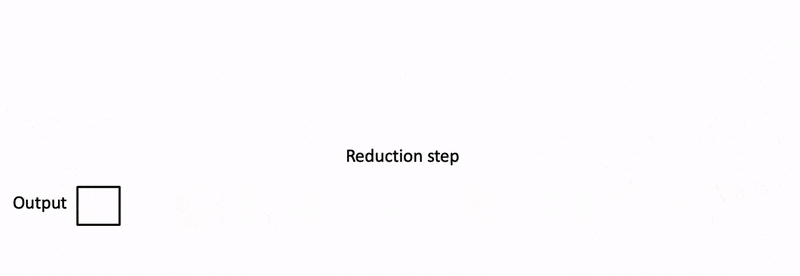
FA2会在Q的seqlen和batch size上做并行,对于每一个Q的分块都会遍历完所有的KV,计算每个局部的Attention结果,并与上一个计算结果结合得到当前的结果。

这种方式在训练OK(seqlen和BS比较大),但inference阶段是逐token生成的,每次只会产生1个token,这就使得GPU利用率极限下降(尤其是BS=1的时候)
FlashDecoding就是在Q,BS无法进一步并行的情况下,对KV进行并行。
- 将KV切成更小的块
- 在这些KV块上执行FA得到局部结果
- 用一个额外的kernel做全局的reduce,得到正确结果
vLLM小记
基本结构
- EntryPoints←数据输入
- Engine←执行核心
- scheduler←调度器,continuous batchng
- KV Cache Manager← page attention核心,LMCache
- worker←各种硬件的worker,worker_base
- core←整个page attention
- prefix caching ←相同前缀的结果直接复用
- CacheBlend←对不完全相同的前缀,但是意思相近的一种复用技术
- KV Cache(MLA)
- Evictor←换入换出策略,LRU
- model Executor(model runner)←llama.py
- modelling←将不同的模型写成框架能懂的形式,推荐llama.py,因为有些新的feature与新的model可能还不兼容
- Attention Backend←flash attention, with kv cache, page attention
分布式推理优化(非PD分离)
分布式推理类型:TP/PP/EP/DP
通信设备:
- NVLink:GPU之间的直连通信
- Infinity Band:节点之间
- RDMA:Remote direct memory access
- RDMA NIC
- software solustion
- key advantage: 跳过操作系统/0拷贝
通信库vllm/distributed/device_comunicators:
- PyNccl:NVIDIA 通信
- shared memory : OS
- custom allreduce: 用于allredcue操作的kernel
- 假设一共有4台机器
- 开始:每个机器都有一份自己的数据
- 结束:每个机器都有4份数据(自己的一份+来自其他3台机器的数据)
- torch.distributed
Tensor Parallel
vllm/model_executor/models/llama.py- All_gather实现集成在Linear中
- Linear计算:(MxK) x(KxN)→(NxM)的矩阵计算过程
- TP计算过程就是在K维度进行切分,每次计算得到
- (MxK’)x(K’xN)->(NxM),这里虽然是(NxM),但是只是实际结果的一部分,最后要用all_gather把他们都加起来
Pipeline Parallel
- PP是不直接降低延迟的,但是TP可以
- 算法:
- worker只在一些层的自己上执行
- 关键标记:self.start_layer →self.end_layer
- get_pp_group()
Expert Parallel & Data Parallel
- MOE架构中使用 Mixtrue of Expert
- 只是一些线性层
- Normal model: 计算所有的权重分区
- MoE:只激活一小部分的权重分区,即被选中的Expert
- 放置不同的expert到不同的GPU上→expert parallel
- EP算法:
- Shuffle(deepep comunication kernel)
- Forward
- Shuffle back(负载均衡,万一全都激活同一个Expert不就只有一台机器工作了)
- TP是用于attention的,EP是用于线性层的
- shared expert每个process都要使用,所以会复制这个expert
- DP
- 条件:TP的数量远小于EP的数量,TP的数量小于attention head的数量,线性层的并行度远远大于attention tp的并行度
- 原因:大概思路就是,Exerpt很多比如用了10台机器,但是我TP的性能只能提供3台机器,这时候就有7台机器闲置了,通过输入不同的数据(DP),让闲置的机器动起来,就可以解决TP和EP不匹配的问题了
- request padding to avoid deadlock
- 为啥要填充输入?比如我有8台机器,但是我只有7个输入,由于每一台机器上都是相同的代码,接收到7个输入之后只有7个机器在运作,一个机器在等待输入,这时候7个机器的东西处理完后,要和其他机器通信,如果这时候和正在等待输入的机器进行通讯,这个正在等待输入的机器是处理不了的,因为他在卡I/O,所以需要一个空的输入去激活这个机器,以便后续的通信计算。
PD分离
什么是prefill和decode
- prefill:对于输入文本处理好所有的输入,并生成对应的KV Cache(处理输入,生成kv cache)
- decode:基于KV cache生成token
为什么要PD分离?
- prefill:attention执行N个tokens,QKV→生成KV cache(compute bound)
- decde:attention N个KV,1个Q →生成一个新的token,very fast (memory bound)
- 初始逻辑:优先prefill(decode会被prefill给拦住)
- problem: prefill将中断其他request的decode
- solution:
- PD分离:一组GPU跑P,另一组GPU跑D(XPXD,PD数量相同,XPYD,PD数量不相同)
- chunked prefill:算子level模糊PD,处理不同shape的attention计算(chunk size过大会导致generate token 速度变慢,过小会导致GPU利用率降低)
PD分离:
有P P node接收request,做inference,将kv cache发送给D node。D node要接收request,基于P node传过来的KV cache在做inference
关键问题:
- 如何传输KV cache?
- pooling mode
- sender 将kv cache写入pool中,receiver从pool中读取kv cache
- sender和receiver都需要保持和pool的连接,并且要有一个比较高的带宽
- p2p mode:sender和receiver需要知道目标是谁,并建立连接进行传输
- Library:LMCache(both),MoonCake(pooling),NIXL(p2p)
- pooling mode
- 如何从框架中extract和inject KV cache ?
- connector API
- called in model_runner(simple_connector.py)
- before model forward : 尝试接收kv cache(注入kv cache到vLLM’s paged memory)
- model forward
- after model forward: 从vLLM’s paged memory提取KV cache,并发送给其他节点
- 什么时候发送request到P Node和D Node?
- first P then D:P node先算完kv cache,然后router收到信息,将request发給D node继续进行toekn generate
- first D then P:认为token generate是主要事情,request都发给D node,然后D node执行时发现没有KV Cache就转发给P node,等待P node处理完成再继续后续的token generate
Speculative Decoding
-
LLM推理的decode阶段是GPU-memory-bound
- 需要寻找一种方法增加他的计算量,但不会显著增加他的显存访问
-
Solution:直接生成token→猜测多个token和verify
- 每个迭代过程生成的token数
- 猜出3个token,猜对的准确率为2/3
- 有2个token是对的,同时LLM inference会自己生成一个token→3 tokens
- 迭代时间
- Computation:(1 + 3)x →原本只生成一个token,现在变成了升生成1个模型计算的token+3个猜的token
- Memory:
- w/o spec : 模型参数(8x2 GB) + KV Cache (n*100KB)
- w/ spec : 模型参数(8x2 GB)+ KV Cache ((n+3) * 100KB)
- 迭代时间几乎没有发生改变,但增加了吞吐量(1→4)
- 每个迭代过程生成的token数
-
衡量Memory-bound和compute-bound的指标:代数强度,arithmetic intensity
- Definition: FLOPs (floating point per second) / MIPs (memory instrctions)
-
如何猜测token
- N-gram
- Build mapping: 如果最后3个是A,B,C, 则后面2个token为D,E
- To be or not to be, this is a question
- [To be or] → [not to]
- [be or not] → [to be]
- …
- [, this is] → [a, question]
- 为输入构建N-grand,使用这个N-gram去猜测输出的tokens
- 生成token时,发现部分满足上面的规则,就会直接应用规则去生成token
- 然后使用LLM进行验证
- model-base: MLP & Medusa
- Parallel guessing
- good : fast
- Bad : 猜测第二个token不需要知道第一个token
- Autorgressive guessing
- good: 猜测第二个token的时候需要第一个token
- Bad:slow
- Parallel guessing
- 部署问题(尤其是model-base的方法)
- 小模型需要kv cache,他们如何分配?
- 小模型小,需要一个不同的并行策略
- 不并行,模型在0号GPU, vLLM 强制不同的GPU有相同的GPU内存使用→ 其他GPU有内存浪费
- 为猜测的token预分配 KV cache
- 需要丢弃掉一些错误的token
- sampling → verification
- 最小化开销(n-gram)
- 如何配置要猜多少个token
- 不同的请求区别
- 不同的请求要猜多少个token
- N-gram
-
如何验证猜测的结果是否正确
- Tree verification
- [To be or] → [not to], [sleep in], [go to]
- [To be or] 猜测有多种可能性:[not to], [sleep in], [go to]
- 确定性情况(精确采样):LLM输入结果是完全正确的,并且没有随机性,猜测符合答案就对,不符合就不对
- 非确定性情况(随机采样):当前猜测的概率 > threshold
example
correct case :
Input : [To be or] (已经decode出来了) [not to] (猜测的token)
ps: llm 会告诉你当前的token的下一个token是啥
LLM : [to be or not to]
[to → be]
[be → or]
[or → not] // 猜测正确(验证部分)
[not → to] // 猜测正确
[to → be] // 模型正常输出
error case :
Input : [To be or] (已经decode出来了) [not be] (猜测的token)
LLM : [to be or not be]
[to → be]
[be → or]
[or → not] // 猜测正确(验证部分)
[not → be] // 猜测错误,终止后续结果,将生成当前结果并结束
- Tree verification
Prefix Caching基本推理逻辑
1 | llm.inference( |
KV管理:key→tokens, value→kv cache tensors
1 | class KVCacheStore: |
prefix-based matching:
Tokens1: ABCDE→[kv1, kv2, kv3, kv4, kv5]
Tokens2: ABCDF→[kv1, kv2, kv3, kv4, kv6]
存入token1
kv_cache_store.store(“ABCDE”, [kv1, kv2, kv3, kv4, kv5])
读取token2,要找出在存储空间中满足最长前缀的结果,并输出前缀每个token对应的kv cache
kv_cache_store.retrieve(“ABCDF”)→[kv1,kv2,kv3,kv4]
"ABCDEF"→ “AB”,“CD”,“EF”(会把句子分成多个chunk,然后存储chunked的前缀哈希)
1 | prefix_hash = "" |
Eviction(换入换出):
LRU,LFU
“ABCDEF” --> [“AB”, KV1], [“CD”, KV2], [“EF”, KV3]
会从cache的最后部分去删除,因为删除了前面的部分后面的部分也无法使用了
剩下的部分基本就和LRU,LFU的规则类似
get_computed_blocks(),
- 把request变成一个个blocks,计算每个blocks的cache rate。
- 把prefix cache 传给specialize manager做find_longest_cache_hit
常见问题
-
Transformer架构和传统RNN神经网络相比的优势
-
Transformer 参数量最带的是哪个部分,计算量最大的是哪个部分
1. 参数量最大的部分:Feed-Forward Network (FFN)
原因: FFN层的“中间维度”通常远大于模型本身的隐藏维度(
d_model)。- 结构剖析:一个标准的FFN层由两个线性层和一个激活函数(如ReLU或GELU)组成。
- 第一层:将输入从
d_model维度扩展到d_ff维度(通常是d_model的4倍,即d_ff = 4 * d_model)。 - 第二层:将
d_ff维度投影回d_model维度。 - 参数量计算:
- 第一层参数:
d_model * d_ff - 第二层参数:
d_ff * d_model - 单个FFN层总参数量:
2 * d_model * d_ff = 2 * d_model * (4 * d_model) = 8 * d_model² - 对比:
- 一个自注意力层的主要参数是 Q, K, V 和 Output 四个投影矩阵,每个矩阵的大小是
d_model * d_model。所以总参数量是4 * d_model²。 - 很明显,
8 * d_model²(FFN) >4 * d_model²(Self-Attention)。
由于Transformer模型通常由N个相同的层堆叠而成(例如,GPT-3有96层),而每一层都包含一个FFN和一个自注意力模块,因此FFN部分的总参数量会占据整个模型参数的大部分(通常在2/3左右)。
2. 计算量最大的部分:Self-Attention Mechanism (自注意力机制)
注意:这里说的是计算量(FLOPs,浮点运算次数),而不是参数量。自注意力机制的计算复杂度与序列长度呈二次方关系,这使得它在处理长序列时成为计算瓶颈。
- 计算过程剖析:对于一个长度为
L的序列,其计算步骤如下:
- 计算Q, K, V矩阵:将输入(
L * d_model)分别与三个权重矩阵(d_model * d_model)相乘。计算量约为3 * L * d_model²。 - 计算注意力分数:
Q * K^T,得到一个L * L的矩阵。计算量约为L² * d_model。 - 应用Softmax和加权求和:对注意力分数矩阵进行Softmax计算(计算量约
L²),然后与V矩阵相乘(计算量约L² * d_model)。
- 总计算量:自注意力的总计算量主要取决于第二步和第三步,其复杂度为 O(L² * d_model)。
- 对比:
- FFN层的计算只涉及序列中的每个token独立地进行矩阵乘法(没有token间的交互),其计算复杂度是 O(L * d_model * d_ff) = O(L * d_model²)(因为
d_ff与d_model成正比)。
关键点:虽然FFN的绝对参数量大,但它的计算可以高度并行化,因为每个token的处理是独立的。而自注意力机制的计算必须考虑序列中所有token对之间的关系,这个
L * L的矩阵运算在序列长度L很大时(例如2048, 4096,甚至更长),计算量会急剧膨胀,远远超过FFN部分。