数据库理论(一)——基本概念与关系代数

基本概念

数据库(Database)：长期存储在计算机内的，有组织的，可共享的数据集合

数据库管理系统(DBMS databases management system)：能够有效建立和维护大量数据的强大工具

数据库管理员(DBA)

用户(User)

型：某一类数据的结构和属性的说明

值：型的一个具体赋值

模式(schema):数据库中全体数据的逻辑结构和特征描述

实例：模式的一个具体的值

数据模型的三个层面

概念层面

逻辑层面

物理层面

(逻辑)数据模型 = 数据结构 + 数据操作集合 + 数据完整性约束

关系数据模型 = 关系数据结构 + 关系数据操作集合 + 关系数据完整性约束

数据库的三级结构模式：

模式(Schema)：数据操作

内模式(Internal Schema)：数据存储方式

外模式(External Schema)：视图

关系模型

关系模型的数据结构：关系

关系的本质：二维表

域(Domain)：一组具有相同数据类型的值的集合

元组(Tuple)：关系中的每一行

属性(Attribute)：关系中的每一列

分量(Component)：元组中的每一属性值

基数：多个域做笛卡儿积之后的元组个数，计算方式为 $M = \pi_{i=1}^nm_i$ 其中表示有n个域， $m_i$ 表示第i个域的属性值数量。

关系是元组集合，类似一张二维表

关系模式是型，是静态的；而关系是值，动态变化的

关系模式的表示

关系模式表示为五元组

$R(U,D,dom,F)$

R表示关系名称，U表示属性名集合，D表示值域集合，dom表示属性向域的映射集合，F表示属性间数据的依赖关系集合

关系数据结构的细分概念

候选码：若关系中的某一属性能够的值能够唯一的标识一个元组，而其子集不能，则称该属性组为候选码

主码：若一个关系有多个候选码，则选定其中一个为主码(Primary Key)

1. 主属性（Prime attribute）：候选码的每一个属性称为主属性

2. 非主属性（Non-Prime attribute）：不包含在任何侯选码中的属性称为非主属性

全码：系模式的所有属性构成这个关系模式的候选码
外码：用于与另一个表做自然链接的属性

数据的完整性约束

特定应用场景中的数据需要满足什么规范

使用完整性约束的理由：

需要保证数据的正确性
具体的应用对数据具有不同的要求

关系的三类完整性约束

实体完整性规则：若属性A是基本关系R的主属性，则A不能取空值（NULL）。
参照完整性规则：要使用外码，保证在数据库中的表不被孤立
用户定义的完整性规则：针对某一具体关系数据库的约束条件，反映某一具体应用所涉及的数据必须满足的语义要求。

关系操作

常用的关系操作：

查询：选择，投影，链接，除，并，差，交，笛卡儿积

数据更新：插入，删除，修改

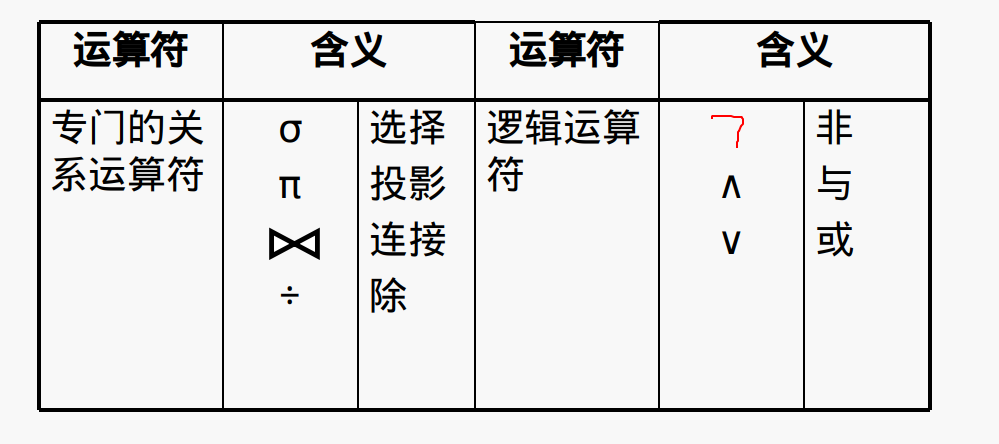
关系代数运算符

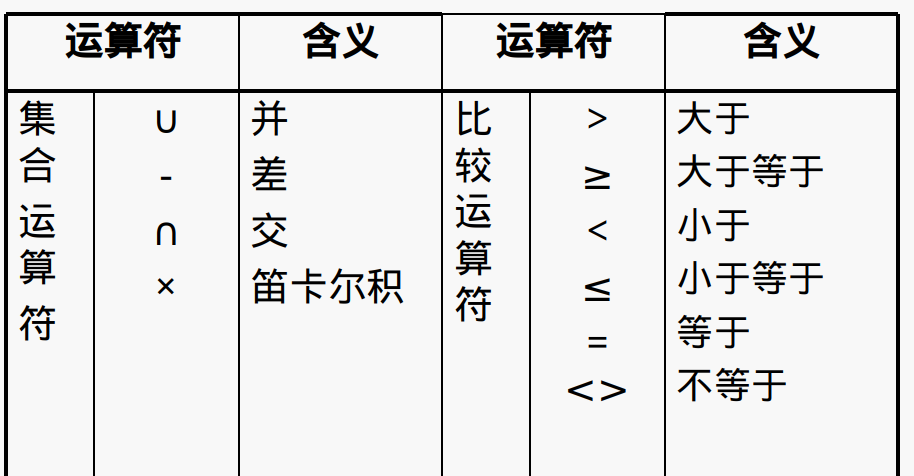
并

生成的关系，属性与R或S相同

元组：在R或S中的元组求并集(去重)

说白了就是拼接

举个例子吧，现在有本科生导师表R，还有研究生导师表S，找出这两个表中所有老师信息就是使用并运算符

差

R,S属性相同

R-S就是在R中不在S中

沿用上面的那个例子，R-S就是找出是本科生导师但不是研究生导师的老师信息，S-R就是找出就是找出是研究生导师但是不是本科生导师的老师信息

交

R,S属性相同

沿用上面的例子，R交S就是值既是本科生导师，又是研究生导师的信息

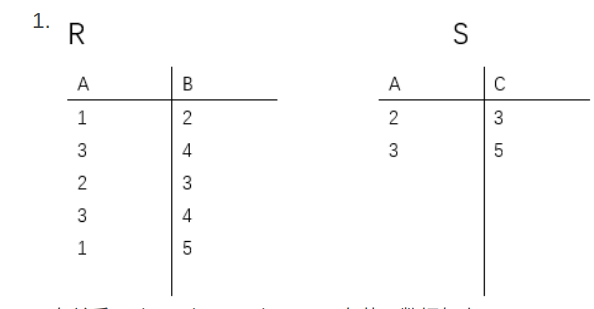
来个例题：

1
2
3

有关系R（A,B),S(A,B), 关系R有m个元组，关系S有n个元组，则R∪S的结果关系最多有几个元组？最少有多少个元组？
那么R∩S的结果关系最多有几个元组？最少有多少个元组？
那么R-S的结果关系最多有几个元组？最少有多少个元组？

R∪S最多，R,S中的元组没有重复的：m+n

R∪S最少，R,S中的元组有一个为其中一个的子集：max(m,n)

R∩S最多，R,S中的元组有一个为其中一个的子集：min(m,n)

R∩S最少，R,S中的元组没有重复的：空集

R-S最多，R,S中的元组没有重复的：m

R-S最少，R包含S时：m-n，S包含R时：空集

笛卡儿积

每个关系看作一个大集合，然后使用遍历R集合中的每一个元组，每次遍历都与S中的每一个元组结合形成新的元组

选择

选行(selection)

$\sigma_c(R)$ 在R集合中选择满足条件c的所有元组

投影

选列(projection)

$\pi_L(R)$ 在集合R中投影出每一个元组中的属于L属性集上的属性值

重命名

$\rho_{A_1,A_2,...,A_n}(R)$

将关系R中的属性重命名为 $A_1,A_2,....$

自然连接

R⋈S

根据R中的外码，连接S

条件连接

$R⋈_{L}S$

遍历R中的元组，然后再遍历S中的元组，如果选择的两个元组满足条件L就合并成新的元组，注意不要去掉重复的列

(我也不确定这样对不对)

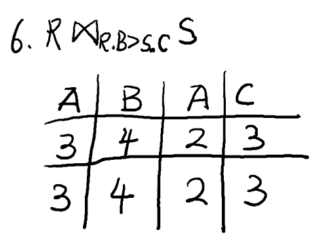
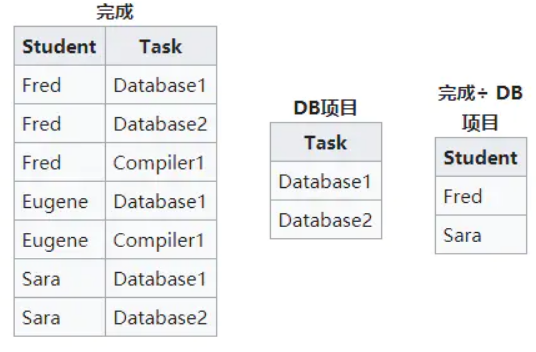
除

A $\div$ B

看图吧：fred有Database1和Database2，Eugene有Database1，Sara有Database1和Database2，所以除了之后就只剩fred和sara了

去重

$\delta(R)$ ，去除R中的重复元素

排序

$\tau_L(R)$ ,将R按照L列进行排序

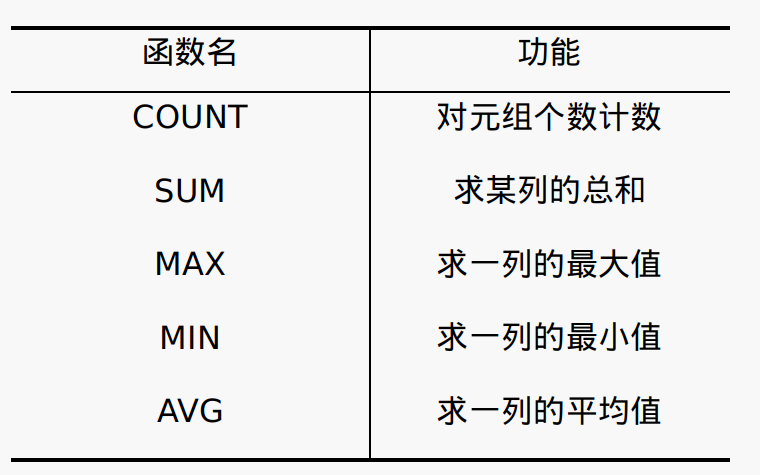
分组与聚集运算符

$\gamma_L(R)$ ，将R按照L的值进行分组，对每个u分组产生一个新的元组

通常分组与聚集运算符一起使用

举个例子：

student(sno,sname,ssex,sage,sdept)

统计一共有多少名学生：

$\gamma_{count(sno)}(student)$

分别统计男生女生各有多少人

$\gamma_{ssex,count(sno)}(student)$

通常对于聚集运算符的结果会重新给其命名，比如上面找出的人数命名为snum

$\gamma_{ssex,count(sno)->snum}(student)$