Region Mutual Information Loss for Semantic Segmentation

论文名称：Region Mutual Information Loss for Semantic Segmentation

作者：Shuai Zhao, Yang Wang, Zheng Yang, Deng Cai

期刊：未查到(2019年)

代码：https://github.com/ZJULearning/RMI

原文摘要

Semantic segmentation is a fundamental problem in computer vision. It is con-sidered as a pixel-wise classification problem in practice, and most segmentationmodels use a pixel-wise loss as their optimization criterion. However, the pixel-wise loss ignores the dependencies between pixels in an image. Several ways toexploit the relationship between pixels have been investigated,e.g., conditionalrandom fields (CRF) and pixel affinity based methods. Nevertheless, these methodsusually require additional model branches, large extra memories, or more inferencetime. In this paper, we develop a region mutual information (RMI) loss to modelthe dependencies among pixels more simply and efficiently. In contrast to thepixel-wise loss which treats the pixels as independent samples, RMI uses one pixeland its neighbour pixels to represent this pixel. Then for each pixel in an image,we get a multi-dimensional point that encodes the relationship between pixels, andthe image is cast into a multi-dimensional distribution of these high-dimensionalpoints. The prediction and ground truth thus can achieve high order consistencythrough maximizing the mutual information (MI) between their multi-dimensionaldistributions. Moreover, as the actual value of the MI is hard to calculate, wederive a lower bound of the MI and maximize the lower bound to maximize thereal value of the MI. RMI only requires a few extra computational resources inthe training stage, and there is no overhead during testing. Experimental resultsdemonstrate that RMI can achieve substantial and consistent improvements inperformance on PASCAL VOC 2012 and CamVid datasets.

摘要

问题描述：语义分割是计算机视觉中的一个基本问题，被认为值一个按照像素进行分类的问题。

研究现状：大多数分割模型使用按像素进行计算的损失作为其优化标准，但是却忽略了像素之间的依赖关系。现在利用像素之间关系的方法有，条件随机场(CRF)和基于像素亲和力(pixel affinity)的方法。但是这种方法通常需要额外的模型分支，或者大量的内存，或者更长的推理时间。

解决方案：本文提出了一种区域互信息(region mutual information RMI)损失函数，以更简单且有效地建立像素间的依赖关系。与将像素视为独立样本的像素损失相反，RMI使用一个像素和他的邻居像素来代表这个像素。然后，对于图像中的每个像素，我们得到一个多维的点来编码像素之间的关系，而图像被投射到这些高维的多维分布中。i因此，预测和ground truth可以通过最大化其多维分布之间的互信息(mutual information MI)来实现高阶一致性。此外，由于MI的实际值很难计算，但是可以得到MI的下限，并将下限最大化，从而使MI的实际值最大化。RMI在训练阶段只需要一些额外的计算资源，在测试阶段则没有开销。

结论：实验结果表名，在PASCAL VOC 2021和CamVid数据集上，RMI可以实现大幅度和持续的性能改进。

介绍

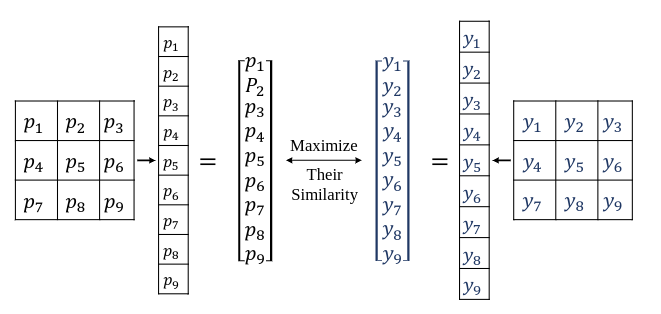
将一张图片的每个像素点，与其周围的8个像素点(没有就Padding)合并成一个9维的向量，这个向量称为9-D，通过最小化ground truth与预测结果在每个像素点之间的9-D差距最小，达到模型优化的目的，其过程可以用下图表示。

熵和互信息(Entropy and mutual information)

令X为一个离散随机变量，字母为 $\mathcal{X}$ ，他的概率质量函数(probability mass function PMF)为 $p(x)$ ，且 $x \in \mathcal{X}$ 。为方便起见，使用 $p(x)$ 和 $p(y)$ 表示两个不同的随机变量，而他们实际上是两个不同的PMF，分别为 $p_X(x)$ 和 $p_Y(y)$ ，X的熵可以表示为公式1:

$公式1: H(X)=-\sum_{x \in \mathcal{X}} p(x) \log p(x)$

熵是对随机变量不确定性的一种衡量。联合熵 $H(X,Y)$ 和条件熵 $H(Y|X)$ ，可表示为一对离散随机变量 $(X,Y)$ 和联合分布 $p(x,y)$ 以及条件分布 $p(y|x)$ 的组合，可以表示为公式2和公式3

$公式2:H(X, Y)=-\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log p(x, y)$

$公式3:H(Y \mid X)=-\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log p(y \mid x)$

事实上，一对随机变量的熵是一个随机变量的熵加上另一个随机变量的条件熵。可表示为公式4:

$公式4：H(X, Y)=H(X)+H(Y \mid X)$

现在介绍互信息(MI)，他是衡量X和Y相互之间所包含的信息量的指标，被定义为公式5:

$公式5:I(X ; Y)=\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x, y) \log \frac{p(x, y)}{p(x) p(y)}$

公式6表示 $I(X;Y)$ 是一个非常自然的依赖性措施，可以被认为是由于对Y的了解而减少了X的不确定性，反之亦然。

$公式6:I(X ; Y)=H(X)-H(X \mid Y)=H(Y)-H(Y \mid X)$

方法介绍

如介绍的图中所示，我们有两个多变量的随机变量 $P=[p_1,p_2,...,p_d]^T$ 和 $Y=[y_1,y_2,...,y_d]^T$ ，其中 $\boldsymbol{P} \in \mathbb{R}^{d}$ 是预测的概率， $\boldsymbol{Y} \in \mathbb{R}^{d}$ 表示ground truth， $p_i$ 在0到1之间， $y_i$ 为0或者为1，若方形区域的尺寸为 $R\times R$ ，且 $d = R\times R$ 。 $\boldsymbol{P}和\boldsymbol{Y}$ 概率密度函数(PDF)表示为 $\mathcal{f}(p)和\mathcal{f}(y)$ 。联合概率密度函数表示为 $\mathcal{f}(y,p)$ 。 $\boldsymbol{P}$ 分布可以表示为 $p_1,p_2,...,p_d$ 的联合分布，可表示为 $f(p)=f(p_1,p_2,...,p_d)$ ，互消息(MI)可以表示为公式7:

$公式7:I(\boldsymbol{Y} ; \boldsymbol{P})=\int_{\mathcal{Y}} \int_{\mathcal{P}} f(y, p) \log \frac{f(y, p)}{f(y) f(p)} \mathrm{d} y \mathrm{~d} p$

其中 $\mathcal{Y}和\mathcal{P}$ 分别是 $\boldsymbol{Y}和\boldsymbol{P}$ 的集合，我们的目的是使得 $I(\boldsymbol{Y};\boldsymbol{P})$ 实现 $\boldsymbol{Y}$ 和 $\boldsymbol{P}$ 的高度一致性。

为了获取互消息(MI)，一个直接的办法就是获取上述的概率密度函数，然而，这些随机变量 $p_1,p_2,...,p_d$ 是依赖的，就像图像中的像素是依赖性的。这就导致他们的联合密度函数 $f(p)$ 变得难以解析。经过前人的证明，对于灰度图来说，当R足够大时，Y和P是正态分布。然而，在本文的实验过程中发现，当Y和P是正态分布时，变长R会变得非常大，比如 $R\geq30$ 。这种情况下维度d就会大于900，内存消耗就会变得非常大，因此使用这种方法的实现是不现实的。由于这些因素，本文得出了 $I(Y;P)$ 的下限，并将下限最大化，使 $I(Y;P)$ 的实际值最大化。

互信息的下限(a lower bound of mutual information)

正态分布在所有具有相同协方差的分布上的熵最大。以及具有协方差矩阵的正态分布的熵 $\boldsymbol{\Sigma} \in \mathbb{R}^{d \times d}为 \frac{1}{2} \log \left((2 \pi e)^{d} \operatorname{det}(\boldsymbol{\Sigma})\right)$ 其中 $det(\cdot)$ 是该矩阵的行列式，因此可以得到一个互信息(MI)的下限。

$公式8:\begin{aligned} I(\boldsymbol{Y} ; \boldsymbol{P}) &=H(\boldsymbol{Y})-H(\boldsymbol{Y} \mid \boldsymbol{P}) \geq H(\boldsymbol{Y})-\frac{1}{2} \log \left((2 \pi e)^{d} \operatorname{det}\left(\boldsymbol{\Sigma}_{Y \mid P}\right)\right) \end{aligned}$

其中 $\sum_{Y|P}$ 是Y鉴于P的后验协方差矩阵，是一个对称的正半定矩阵。结合交叉熵损失函数和去除与模型无关的参数后，可以得到一个简化的下限：

$公式9:I_{l}(\boldsymbol{Y} ; \boldsymbol{P})=-\frac{1}{2} \log \left(\operatorname{det}\left(\boldsymbol{\Sigma}_{Y \mid P}\right)\right)$

后验方差的近似值(an approximation of posterior variance)

现在的关键问题，就变成了找出后验协方差矩阵 $\sum_{Y|P}$ 。然而我们无法获得准确地获得 $\sum_{Y|P}$ ，因为我们不知道Y和P的概率密度函数还有他们的依赖项。

幸运的是已经有人给出了贝叶斯推理中某个假设下的后验变量的近似值。

对于给定的P要估计Y

$\mathbb{E}(\boldsymbol{Y})$ 是Y的平均向量(也叫做 $\mu_y$ )

$Var(\boldsymbol{Y})$ 是Y的方差矩阵(也叫做 $\sum_Y$ )

$Cov(\boldsymbol{Y},\boldsymbol{P})$ 是 $\boldsymbol{Y}$ 和 $\boldsymbol{P}$ 的协方差矩阵

用记号 $\boldsymbol{Y} \perp_{2} \boldsymbol{P}$ 表示Y和P是二元线性无关的

对于$ \boldsymbol{P}中的任意一个p的值，都有\mathbb{E}(\boldsymbol{Y} \mid \boldsymbol{P}=p)=\mathbb{E}(\boldsymbol{Y})和\operatorname{Var}(\boldsymbol{Y} \mid \boldsymbol{P}=p)=\operatorname{Var}(\boldsymbol{Y})$

二阶独立性是一个比较严格的相互独立性更若的约束

其引入了Y在P上的回归矩阵(regression matrix)， $A_{yp}=\operatorname{Cov}(\boldsymbol{Y}, \boldsymbol{P}) \boldsymbol{\Sigma}_{P}^{-1} 。通过计算\boldsymbol{Y}-A_{y p} \boldsymbol{P}和\boldsymbol{P}$ 的线性相关系数，可以很容易地发现他们是不相关的。

为了获得后验协方差的近似值 $\operatorname{Var}(\boldsymbol{Y} \mid \boldsymbol{P}=p)$ ，假设 $\left(\boldsymbol{Y}-A_{y p} \boldsymbol{P}\right) \perp_{2} \boldsymbol{P}$ (这个假设意味着 $Var(\boldsymbol{Y}-A_{yp}\boldsymbol{P})\perp_{2}\boldsymbol{P}$ 不依赖于 $\boldsymbol{P}$ 上的值)，

根据n写法观察矩阵的属性和二阶独立性的定义，可以得到公式10:

$公式10:Var(\boldsymbol{Y}|\boldsymbol{P}=p)=Var(\boldsymbol{Y}-A_{yp}\boldsymbol{P}|\boldsymbol{P}=p)\\ = Var(\boldsymbol{Y}-A_{yp}\boldsymbol{P})\\ = \sum_Y-Cov(\boldsymbol{Y},\boldsymbol{P})(\sum_P^{-1})^{T}Cov(\boldsymbol{Y},\boldsymbol{P})^T$

定理1：考虑上述的随机变量 $\boldsymbol{Y}$ 和 $\boldsymbol{P}$ ，在二元损失下， $\mu_y+A_{yp}(\boldsymbol{P}-\mu_p)$ 是贝叶斯线性估计器，当且仅当随机变量满足条件 $\left(\boldsymbol{Y}-A_{y p} \boldsymbol{P}\right) \perp_{2} \boldsymbol{P}$

在之前的假设和定理1的情况下，我们可以得到线性最小均方差(MMSE)估计器，这也表名，后验方差的近似值(公式10)和真实的后验方差之间的差异被限制在一定范围内。否则， $\mathbb{E}(\boldsymbol{Y} \mid \boldsymbol{P})=\boldsymbol{\mu}_{y}+A_{y p}\left(\boldsymbol{P}-\boldsymbol{\mu}_{p}\right)$ 不能是线性MMSE估计器。

现在我们可以得到公式9的近似值

$公式11:I_{l}(\boldsymbol{Y} ; \boldsymbol{P}) \approx-\frac{1}{2} \log \left(\operatorname{det}\left(\boldsymbol{\Sigma}_{Y}-\operatorname{Cov}(\boldsymbol{Y}, \boldsymbol{P})\left(\boldsymbol{\Sigma}_{P}^{-1}\right)^{T} \operatorname{Cov}(\boldsymbol{Y}, \boldsymbol{P})^{T}\right)\right)$

为了简洁起见，令 $\boldsymbol{M}=\boldsymbol{\Sigma}_{Y}-\operatorname{Cov}(\boldsymbol{Y}, \boldsymbol{P})\left(\boldsymbol{\Sigma}_{P}^{-1}\right)^{T} \operatorname{Cov}(\boldsymbol{Y}, \boldsymbol{P})^{T}$ 且 $\boldsymbol{M} \in \mathbb{R}^{d \times d}$ ，其是一个正半定矩阵，因为他是 $\boldsymbol{Y}-A_{y p} \boldsymbol{P}$ 的协方差矩阵

实现细节

下采样(Downsampling)

和介绍的图一样，在一个大小为 $\mathcal{R} \times \mathcal{R}$ 的正方形区域内选择像素，构建一个多维分布。如果 $\mathcal{R} =3$ ，将导致9倍的内存消耗。对于一个形状为[16,513,513,21]的浮点型张量，其原始内存用量约为0.33GB，而使用RMI时，这一用量变成了约为 $9\times0.33=2.97GB$ ，这也意味着更多的浮点运算，我们无法承受如此大的计算资源成本，所以本位对ground truth和pred概率进行了下采样，以节省资源，但对性能的牺牲很小。

归一化(Normalization)

对于公式11，我们得到 $\log (\operatorname{det}(\boldsymbol{M}))=\sum_{i=1}^{d} \log \lambda_{i}$ 其中 $\lambda$ 是M的特征值，不难看出， $I_{l}(\boldsymbol{Y} ; \boldsymbol{P})$ 的大小很可能与M的特征值的数量有关。为了使 $I_{l}(\boldsymbol{Y} ; \boldsymbol{P})$ 的值归一化，我们把他除以d，如公式12所示

$公式12:I_{l}(\boldsymbol{Y} ; \boldsymbol{P}) \approx-\frac{1}{2 d} \log (\operatorname{det}(\boldsymbol{M}))$

下溢问题(Underflow issue)

由softmax或sigmoid操作给出的概率的大小可能非常小，同时，点的数量可能非常大，因此我们使用公式 $Cov(\boldsymbol(Y),\boldsymbol(Y))=\mathbb{E}\left(\left(\boldsymbol{Y}-\boldsymbol{\mu}_{y}\right)\left(\boldsymbol{Y}-\boldsymbol{\mu}_{y}\right)^{T}\right)$ 去计算协方差矩阵。矩阵中的一些小条目会有极小的数值，我们在计算公式12中协方差矩阵的行列式时可能会遇到下溢的问题，于是我们改写公式12为公式13

$公式13:I_{l}(\boldsymbol{Y} ; \boldsymbol{P}) \approx-\frac{1}{2 d} \operatorname{Tr}(\log (\boldsymbol{M}))$

其中 $Tr(\cdot)$ 是矩阵的迹，此外，M是一个对称正半定矩阵。在实践过程中，本文在M的对角线上添加一个小的正常数，然后得到 $M = M + \xi I$ ，其中 $\xi$ 在实践中为1e-6。这个操作对i系统优化影响不大，但是可以通过对M进行Cholesky分解来加速公式13的计算，因为现在M是对称正定矩阵。值得注意的是，当M是正定的时候， $log(det(M))$ 是凹函数，这使得RMI容易优化。

总体目标函数（overall objective function）

用于训练的目标函数可以用公式14表示

$公式14：\mathcal{L}_{\text {all }}(y, p)=\lambda \mathcal{L}_{c e}(y, p)+(1-\lambda) \frac{1}{B} \sum_{b=1}^{B} \sum_{c=1}^{C}\left(-I_{l}^{b, c}(\boldsymbol{Y} ; \boldsymbol{P})\right)$

其中 $\lambda \in[0,1]$ 是一个权重因子， $\mathcal{L}_{c e}(y, p)$ 是y和p之间的正常交叉熵， $B$ 表示batch-size的大小，而RMI的最大化被投射为一个最小化问题。正态交叉熵损失的左右是衡量两幅图像的像素密度之间的相似性，而RMI可以被认为是衡量两幅图像的结构相似性。按照结构相似性(SSIM)指数，像素i相似性和结构相似性的重要性被同等考虑，所以我们简单地设置 $\lambda=0.5$

我们采用的sigmoid运算而不是softmax运算来获得预测概率，这是因为RMI是按通道范围(channel-wise)计算的，我们不希望在信道之间引入干扰。实验结果表名，用softmax和sigmoid交叉熵损失训练的模型的性能大致相同。

实验步骤

基本模型：DeepLabV3和DeepLabV3+作为基本模型，DeepLabV3+比DeepLabV3添加一个解码器模块来完善分割结果，骨干是ResNet-101，最初的一个7x7卷积层被替换成3个3x3卷积。

数据集：我们在两个数据集上评估了我们的方法，PASCAL VOC 2012和CamVID数据集。

学习率和训练步骤：采用warm up学习率策略和poly学习率策略，如果初始学习率为lr，当前迭代步骤为iter，学习率为 $lr \times \frac {iter}{slow_iters}$ ，对于其余的步骤的学习率为 $lr \times (1-\frac {iters-slowIters}{maxIter-slowIters})^{power}$ 其中，power=0.9，maxIter为训练的最大步数。在VOC中，迭代次数为30K,lr=0.007,slowIters=1.5K。在CamVid中，迭代次数为6K，lr=0.025，slowIter=300。

裁剪尺寸和输出步长：在训练过程中，批次大小始终为16，VOC和CamVid的裁剪量为513和479。输出步长，即输入图像空间分辨率与最终输出分辨率纸币，在训练和推理过程中始终为16.在计算损失函数时，将logits(softmax或sigmoid运算前的模型输出)上采样为输入图像的分辨率，而不是将其下采样。

数据增强：在训练过程中通过随机缩放输入图像和随机左右翻转来应用数据增强，在VOC上，随机比例为 $[0.5,0.75,1.0,1.25,1.50,1.75,2.0]$ ，在CamVid数据集a输尿管为0.75~1.25，然后我们对数据进行标准归一化处理，使其均有0均值和1方差。