FaPN: Feature-aligned Pyramid Network for Dense Image Prediction

论文：FaPN: Feature-aligned Pyramid Network for Dense Image Prediction

作者：Shihua Huang, Zhichao Lu, Ran Cheng, Cheng He

期刊： ICCV2021

代码：https://github.com/EMI-Group/FaPN

原文摘要

Recent advancements in deep neural networks havemade remarkable leap-forwards in dense image prediction.However, the issue of feature alignment remains as ne-glected by most existing approaches for simplicity. Directpixel addition between upsampled and local features leadsto feature maps with misaligned contexts that, in turn, trans-late to mis-classifications in prediction, especially on ob-ject boundaries. In this paper, we propose a feature align-ment module that learns transformation offsets of pixelsto contextually align upsampled higher-level features; andanother feature selection module to emphasize the lower-level features with rich spatial details. We then integratethese two modules in a top-down pyramidal architectureand present the Feature-aligned Pyramid Network (FaPN).Extensive experimental evaluations on four dense predic-tion tasks and four datasets have demonstrated the efficacyof FaPN, yielding an overall improvement of 1.2 - 2.6 pointsin AP / mIoU over FPN when paired with Faster / Mask R-CNN. In particular, our FaPN achieves the state-of-the-artof 56.7% mIoU on ADE20K when integrated within Mask-Former.

摘要

问题：大多数现有的方法仍然忽略了特征对齐问题，上采样和局部特征之间的直接像素相加导致特征图的上下文不一致，反过来又会转化为预测中的错误分类，特别是在物体的边界上。

本文工作：提出了一个特征对齐(feature alignment)模块，该模块学习像素的转换偏移量，以便在上下文中对齐上采样的高层特征。令一个特征选择模块强调具有丰富空间细节的低层次特征。然后将这两个模块整合到一个自上而下的金字塔结构中，并提出了特征对齐金字塔(Feature-aligned Pyramid Network FaPN)。

介绍

密集预测(dense prediction)需要丰富的空间细节来确定物体的位置，也需要强大的语义来进行物体分类，这些细节通常来自不同的分辨率/尺度。如何有效地生成不同尺度的特征层次，称为处理密集预测任务时需要克服的关键任务之一。

这种问题通常有两种常见的做法来解决，第一种做法是使用不同空洞率(different atrous rates)的空洞卷积(atrous convolution)，在不降低空间分辨率的情况下有效地捕捉长距离信息(即语义背景)。另一种是基于卷积网络默认底层路径建立一个自上而下的特征金字塔。更具体地说，在来自自下而上途径的相应特征图合并之前，对（更高级别的）空间上更粗的特征图进行上采样。然而，由于常用的上采样操作(如最邻近)的不可学习性以及下采样和上采样的重复应用，自下而上和上采样的特征之间存在不准确的对应关系(即特征错位)。错位的特征反过来又会对后续层的学习产生不利影响，导致最终预测的错误分类，特别是在物体边界附近。

为解决上述问题，本文提出了特征对齐模块(feature alignment module)，该模块通过调整卷积核中的每个采样位置，学习将上采样的特征图与一组参考特征图对齐。我们进一步提出了一个特征选择模块，以适应性地强调含有过多空间细节的自下而上的特征图，从而实现准确定位。然后，将这个模块整合到一个自上而下的金字塔结构中，并提出特征对齐金字塔网络(FaPN)

特征对齐的金字塔网络(Feature-aligned Pyramid Network)

网络包含两个模块——特征选择模块(FSM)和特征对齐模块(FAM)。其结构图如下所示：

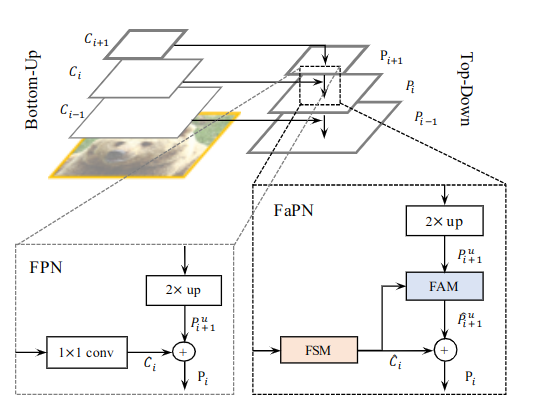
具体来说，将自下而上(Botton-Up)网络第i阶段的输出定义为$C_i$，他相对与输入图像有$2^i$像素的跨度，即$\mathbf{C}_{i} \in \mathbb{R}^{\frac{H}{2^{i}} \times \frac{W}{2^{i}}}$,其中$W\times H$表示图片的长宽。为简洁起见，使用$(H_i,W_i)$表示$(\frac H{2^i},\frac W{2^i})$。使用$\hat{\mathbf{C}}_{i}$表示$C_i$输入FSM层的输出。同时在自上而下的途径中，第i个特征融合后的输出被定义为$P_i$，其上采样和i对齐的特征到$C_{i-1}$的输出分别为$P_i^u$和$\hat{P_i^u}$

特征对齐模块(Feature Alignment Module)

由于递归地使用下采样操作，上采样的特征图$P_i^u$和相应的下采样的特征图$C_{i-1}$之间存在可预见的空间错位。因此，通过元素加法或通道拼接法进行的特征融合会损害物体边界周围的预测。在进行特征聚合之前将$P^u_i$与它的参照物$\hat{C}_{i-1}$对齐非常重要，即根据$\hat{C}_{i-1}$所提供的空间位置信息来调整$P^u_i$。在这项工作中，空间位置信息由二维特征图呈现，其中每个偏移值可以被看作是$P^u_i$中的每个点与$\hat{C}_{i-1}$中的对应点在二维空间中的位移距离。

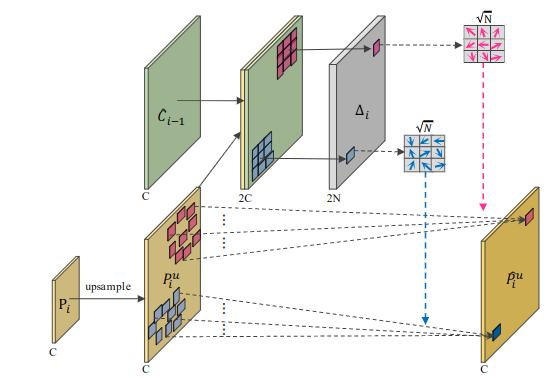
如上图所示，特征对齐可以用数学方法表述为公式1：

$$公式1：\begin{aligned} \hat{\mathbf{P}}_{i}^{u} &=f_{a}\left(\mathbf{P}_{i}^{u}, \boldsymbol{\Delta}_{i}\right) \\ \boldsymbol{\Delta}_{i} &=f_{o}\left(\left[\hat{\mathbf{C}}_{i-1}, \mathbf{P}_{i}^{u}\right]\right) \end{aligned}$$

其中$\left[\hat{\mathbf{C}}_{i-1}, \mathbf{P}_{i}^{u}\right]$是拼接$\hat{\mathbf{C}}_{i-1}和 \mathbf{P}_{i}^{u}$从而提供上采样和相应自下而上的特征之间的空间差异。$f_o(\cdot)和f_a(\cdot)$分别表示从空间差异中学习到的偏移量$(\Delta_i)$和用学习到的偏移量对准特征。在这项工作中，$f_a(\cdot)和f_o(\cdot)$是用可变形卷积(deformable convolutions)实现的，然后是相同大小的卷积核的标准卷积进行激活。

偏移域和输入有相同的分辨率，2N个通道分俵表示N个二维偏移(x,y)。N表示N个位置的卷积核。对于一个3x3的卷积来说N=9，每一个值表示第n个偏移域对第n个位置的水平和竖直偏移量。

我们首先定义一个输入特征图$\mathbf{c}_{i} \in \mathbb{R}^{H_{i} \times W_{i}}$和一个KxK的卷积层。然后在卷积和之后的任何位置$\hat{x}_P^*$的输出特征可以通过下面的公式2得到：

$$公式2:\hat{x}_{\mathbf{p}}=\sum_{n=1}^{N} w_{n} \cdot x_{\mathbf{p}+\mathbf{p}_{n}}$$

N=KxK（卷积核的大小为KxK），$w_n$和$P_n\in \left\{\left(-\left\lfloor\frac{k}{2}\right\rfloor,-\left\lfloor\frac{k}{2}\right\rfloor\right),\left(-\left\lfloor\frac{k}{2}\right\rfloor, 0\right), \ldots,\left(\left\lfloor\frac{k}{2}\right\rfloor,\left\lfloor\frac{k}{2}\right\rfloor\right)\right\}$分别指的是第n个卷积采样位置的权重和预先指定的偏移，除了预先指定的偏移量，可变形卷积还试图学习额外的偏移量$\left\{\Delta \mathbf{p}_{1}, \Delta \mathbf{p}_{2}, \ldots, \Delta \mathbf{p}_{N}\right.\}$自适应地处理不同的采样点，可以使用下面的公式表示

$$公式3:\hat{x}_{\mathbf{p}}=\sum_{n=1}^{N} w_{n} \cdot x_{\mathbf{p}+\mathbf{p}_{n}+\Delta \mathbf{p}_{n}}$$

其中每个$\Delta P_n$是一个元组(h,w)，$h\in(-H_i,H_i),w\in(-W_i,W_i)$

当我们在$P_i^u$上应用可变卷积并将$\hat{C}_{i-1}$和$P_i^u$的连接作为参考时，可变形卷积可以按照公式1偏移量调整其卷积样本的位置，即根据$\hat{C}_{i-1}$和$P_i^u$之间的空间距离对齐$P_i^u$

Feature Selection Module(特征选择块)

在对细节特征进行通道还原之前，强调包含过多空间细节的重要特征图以进行精准分配，同时抑制多余的特征图是至关重要的。我们没有简单地使用1x1卷积，而是提出了一个特征选择模块(FSM)，明确地对特征图的重要性进行建模，并相应地重新校准它们。提出的FSM模块，其结构如下图所示：

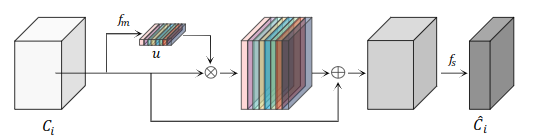
$C_i=[c_1,c_2,...,c_{D^{\prime}}]和\hat{\mathbf{C}}_{i}=\left[\hat{\mathbf{c}}_{1}, \hat{\mathbf{c}}_{2}, \ldots, \hat{\mathbf{c}}_{D^{\prime}}\right]$分别指输入和输出特征图，其中$c_d和\hat{c}_d\in \mathbb{R}^{H_{i}} \times W_{i}$，$D和D^{\prime}$分别指输入和输出通道。$\mathbf{u}=\left[u_{1}, u_{2}, \ldots, u_{D}\right]$是特征重要性向量，其中$u_d$表示第d个输入的特征图的重要性。$f_m$和$f_s$分别代表特征重要性建模和特征选择层。

首先，每个输入特征图的全局信息$z_i$通过全局平均池化操作提取出来，而特征重要性建模$f_m(\cdot)$即1x1卷积层后面加一个sigmoid激活函数，学习使用这些信息为每个特征图的重要性建模，并输出一个重要性向量u。接下来，用重要性向量对原始输入的特征图进行缩放，然后将缩放后的特征图加入到原始特征图中，称为重新缩放的特征图(rescaled feature maps)。最后，在重新标定的特征图上引入特征选择层$f_s(\cdot)$即1x1卷积层，以提高效率，用于有选择地保留重要的特征图，放弃无用的特征图，以减少通道，总之，FSM的过程可以被表述为公式4:

$$公式4:\begin{aligned} \hat{\mathbf{C}}_{i} &=f_{s}\left(\mathbf{C}_{i}+\mathbf{u} * \mathbf{C}_{i}\right) \\ \mathbf{u} &=f_{m}(\mathbf{z}) \end{aligned}$$

其中z的计算方式为公式5:

$$公式5：z_{d}=\frac{1}{H_{i} \times W_{i}} \sum_{h=1}^{H_{i}} \sum_{w=1}^{W_{i}} c_{d}(h, w)$$

值得一提的是，FSM设计是由squeeze-and-excitation(SE)启发的。主要区别在于在输入和缩放的特征图之间引入了额外的跳跃连接。从经验上看，我们发现(通过跳远连接)对比例特征的下限是至关重要的，这可以避免任何特定通道反应被过度放大或压制，从概念上讲，这两个模块都是通过通道注意力来适应性地重新校准通道反应。然而，SE通常用于增强特征提取的主干，而FSML用于增强多尺度特征聚合的颈部(即自上而下的途径)。此外，从FSM中选择/缩放特征也被称作为参考提供FAM，用于学习对齐偏移。