Unifying Nonlocal Blocks for Neural Networks

论文名称：Unifying Nonlocal Blocks for Neural Networks

作者：Lei Zhu, Qi She, Duo Li, Yanye Lu, Xuejing Kang, Jie Hu, Changhu Wang

期刊：ICCV2021

代码：https://github.com/zh460045050/SNL_ICCV2021

原文摘要

The nonlocal-based blocks are designed for capturinglong-range spatial-temporal dependencies in computer vi-sion tasks. Although having shown excellent performance,they still lack the mechanism to encode the rich, struc-tured information among elements in an image or video.In this paper, to theoretically analyze the property of thesenonlocal-based blocks, we provide a new perspective to in-terpret them, where we view them as a set of graph filtersgenerated on a fully-connected graph. Specifically, whenchoosing the Chebyshev graph filter, a unified formulationcan be derived for explaining and analyzing the existingnonlocal-based blocks (e.g., nonlocal block, nonlocal stage,double attention block). Furthermore, by concerning theproperty of spectral, we propose an efficient and robust spec-tral nonlocal block, which can be more robust and flexibleto catch long-range dependencies when inserted into deepneural networks than the existing nonlocal blocks. Experi-mental results demonstrate the clear-cut improvements andpractical applicabilities of our method on image classifica-tion, action recognition, semantic segmentation, and per-son re-identification tasks.

摘要

问题描述：nonlocal的设计由于捕捉计算机视觉任务中的大范围空间和时间依赖。但是其缺乏图像或者视频中各元素之间丰富的结构化信息进行编码的机制。

工作：本文把他看作是一个完全连接的图上生成的一组图过滤。具体来说，当选择切比雪夫图滤波器时，可以得出一个统一的公式来解释和分析现有的非局部区块(例如，nonlocal block，nonlocal stage，双注意力区块)。

此外，通过对频谱属性的研究，本文提出了一种高效，稳健的频谱nonlocal block，与现有的Nonlocal block相比，他在插入到深度神经网络中时，可以更稳健更灵活地捕捉到长距离的依赖关系。

介绍

在实践中，多个卷积运算堆叠出来的感受野存在两个问题：

1. 重复的卷积运算会带来更高的计算和内存成本，以及过拟合的风险
2. 堆叠更多的层不能总是增加有效的感受野

这两个问题表明，卷积层可能仍然缺乏有效模拟这些依赖关系的机制。

Nonlocal Block

nonlocal block计算每个位置的特征和所有可能的位置之间的配对的加权和，其计算方式可以使用公式1表示：

$$公式1:F\left(\boldsymbol{X}_{i,:}\right)=\frac{\sum_{j}\left[f\left(\boldsymbol{X}_{i,:}, \boldsymbol{X}_{j,:}\right) g\left(\boldsymbol{X}_{j,:}\right)\right]}{\sum_{j} f\left(\boldsymbol{X}_{i,:}, \boldsymbol{X}_{j,:}\right)}$$

其中$X \in \mathbb{R}^{N \times C_{1}}$是输入的特征图，i,j是特征图中的位置索引，$f(\cdot)$是具有有限傅里叶规范的亲和核，$g(\cdot)$是一个线性的embedding，定义为公式的计算方式

$$公式2：g\left(\boldsymbol{X}_{j,:}\right)=\boldsymbol{X}_{j,:} \mathbf{W}_{Z}\\ \mathbf{W}_{Z} \in \mathbb{R}^{C_{1} \times C_{s}}$$

其中N表示的是每一个特征的所有位置，$C_1和C_s$是输入和转化特征的通道数。

当把NL块插入到网络结构中时，会添加一个带有权重矩阵$W \in \mathbb{R}^{c_S \times C_1}$的线性变换和一个残差连接被添加，如公式3所示

$$公式3:\boldsymbol{Y}_{i,:}=\boldsymbol{X}_{i,:}+F\left(\boldsymbol{X}_{i,:}\right) \mathbf{W}$$

尽管NL块和视觉变换器(ViT)都利用了自注意力机制，但前者是在CNN的某个阶段加入的，以感知远距离的依赖关系，而不是像后者这样用来取代CNN中的所有卷积计算。

图傅里叶变换和图滤波器(Graph Fourier Transform & Graph Filter)

假设图G包含N个顶点，可以定义一个任意的函数(或信号)向量$\boldsymbol{f}=\left\{f_{1}, f_{2}, \cdots, f_{N}\right\}$，其中向量$f(i)$的第一个分量代表图G第1个顶点的函数值。然后图傅里叶变换$\hat{f}$在G的顶点$f$可以被表述为图拉普拉斯的特征向量拓展，如公式4所示：

$$公式4：\hat{\boldsymbol{f}}\left(\lambda_{l}\right)=\sum_{i=1}^{N} \boldsymbol{f}(i) \boldsymbol{u}_{l}^{*}(i)$$

其中$\boldsymbol{\lambda}=\left[\lambda_{1}, \cdots, \lambda_{l}, \cdots\right]$和$\boldsymbol{U}=\left[\boldsymbol{u}_{1}, \cdots \boldsymbol{u}_{l}, \cdots\right]$是图拉普拉斯的特征值和特征向量。$\hat{f}\left(\lambda_{l}\right)$表示在$u_l,u_l^*$下响应的光谱系数，是$U^T$第l列向量。那么，反图傅里叶变换由公式5给出

$$公式5:\boldsymbol{f}(i)=\sum_{i=1}^{N} \hat{\boldsymbol{f}}\left(\lambda_{l}\right) \boldsymbol{u}_{l}(i)$$

图滤波器是一个运算器，他根据特征值U，按照作用于$\boldsymbol{\lambda}$.的频率响应$g_\theta$来修改输入信号x的成分，因此，基于图傅里叶变换，在图G下过滤x的输出可以被定义为公式6

$$公式6:\boldsymbol{O}(i)_{\boldsymbol{x} *_{\mathcal{g}} \mathbf{g}_{\theta}}=\sum_{l=1}^{N} \hat{\boldsymbol{O}}\left(\lambda_{l}\right) \boldsymbol{u}_{l}(i)=\sum_{l=1}^{N} \hat{\boldsymbol{x}}\left(\lambda_{l}\right) \hat{\mathrm{g}}_{\theta}\left(\lambda_{l}\right) \boldsymbol{u}_{l}(i)$$

其中$\hat{\boldsymbol{x}}, \hat{\mathrm{g}}_{\theta}, \hat{\boldsymbol{O}}$分别是信号，滤波器和输出信号$O_{x *_{\mathcal{G}} \mathrm{g}_{\theta}}$的图傅里叶变换。

非局部区块的光谱观(The Spectral View of Nonlocal-based blocks)

为了定义非局部的光谱观，本文从将非局部算子的矩阵纳入公式3中，将参数矩阵$W$分解为$W_{s1}和W_{s2}$

$$公式7:Y = X + F(X)W = X+AZW_{S1}W_{S2}$$

在这个公式7中，$A = D_M^{-1}M$是亲和矩阵，$M=[m_{ij}]$由像素之间的成对相似性组成，即$M_{ij}=f(X_{i,:},X_{j,:})$，其中$f(\cdot)$ 表示点乘。$D_M$是一个对角矩阵，包含M的每个顶点的程度，$Z=XW_Z \in \mathbb{R}^{N\times C_s}$是转移的特征图，通过线性变换压缩X的通道$W_Z \in \mathbb{R}^{C_1\times C_s}。W_{s1} \in \mathbb{R}^{C_s\times C_s},W_{s2} \in \mathbb{R}^{C_s\times C_1}$是两个参数矩阵，分别用于过滤鉴别特征和恢复通道数。

然后基于公式7，非局部块可以通过将$W_{s1}$概括为一组图滤波器$\mathbf{g}_{\theta}=\left\{\mathbf{g}_{\theta}^{1}, \cdots, \mathbf{g}_{\theta}^{i}, \cdots, \mathbf{g}_{\theta}^{C_{s}}\right\}$而在光谱观点中得到表述

$$公式8:\boldsymbol{Y}=\boldsymbol{X}+\mathcal{F}\left(\boldsymbol{A}, \boldsymbol{Z}, \mathbf{W}_{s 1}\right) \mathbf{W}_{s 2}=\boldsymbol{X}+\mathcal{F}\left(\boldsymbol{A}, \boldsymbol{Z}, \mathbf{g}_{\theta}\right) \mathbf{W}_{s 2}$$

其中$F(A,Z,g_{\theta})$是谱系视角下的非局部算子(nonlocal operation in the spectral view)，为了清楚期间，我们省略$W_{s2}$，假设$C_1=C_s$，将$F(A,Z,g_\theta)$缩写为$F(A,Z)$，并在下文中称之nonlocal算子。

在这种观点中，非本地算子首先计算定义图谱的亲和矩阵A，然后学习图谱特征的过滤器$g_\theta$。具体来说，构建一个完全连接的图$G=\{V,A,Z\}$，其中$\mathbb{v}$是顶点集，然后对于Z的每一个列向量，$z_i \in \mathbb{R}^{N\times1}$生成一个图滤波器$g_{\theta}^i$，以提高特征辨别能力。从这个角度来看，非局部运算器在理论上可以用光谱的观点来解释如下：

定理1：给定一个亲和矩阵$A \in \mathbb{R}^{N\times N}$和信号$Z \in \mathbb{R}^{N \times C}$，非局部算子用一组滤波器$\left\{\mathbf{g}_{\theta}^{i}, \mathbf{g}_{\theta}^{2}, \cdots, \mathbf{g}_{\theta}^{C}\right\}$在完全连接图G的图域下过滤信号Z是一样的。

$$公式9:\mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\left[\boldsymbol{O}_{\boldsymbol{z}_{1} * \mathcal{g} \mathbf{g}_{\theta}^{1}}, \cdots, \boldsymbol{O}_{\boldsymbol{z}_{i} *_{\mathcal{G}} \mathbf{g}_{\theta}^{i}}, \cdots, \boldsymbol{O}_{\boldsymbol{z}_{C *} \mathfrak{g}_{\theta}^{C}}\right]$$

其中图$G=(V,Z,A)$有顶点集V，节点特征Z和亲和矩阵A，$\boldsymbol{O}_{\boldsymbol{z}_{i} * \mathcal{G} \mathbf{g}_{\theta}^{i}} \in \mathbb{R}^{N \times 1}$是$z_i$上的输出信号。

具体来说，每一列向量Z的输出信号的广义实现可用于定理1，将图谱滤波器设置为一组对角线参数矩阵$\mathbf{\Omega}^{i} \in \mathbb{R}^{N \times N}$

$$公式10:\boldsymbol{O}_{\boldsymbol{z}_{i} *_{\mathcal{G}} \mathbf{g}_{\theta}^{i}}=\boldsymbol{U} \boldsymbol{\Omega}^{i} \boldsymbol{U}^{\top} \boldsymbol{z}_{i}$$

其中$\mathbf{\Omega}^{i}=\operatorname{diag}\left(\left[\omega_{1}, \omega_{2}, \cdots, \omega_{n}\right]\right)$包含n个参数，此外，新的非局部算子也可以在理论上通过使用不同类型的滤波器来获得定理1中输出信号。比如Chebyshev滤波器，graph wavelet滤波器，Cayley滤波器。

统一现有的Nonlocal-base Blocks

本文锁提出的光谱观提供了一个有效的工具，在图信号处理的基础上分析实验设计的Nonlocal block。为了统一基于定理1的其他nonlocal block，这里使用了切比雪夫滤波器来说明，即用切比雪夫多项式将$\Omega^{i}$中的参数减少为K，为了简单起见，我们首先假设输入和输出信号都有一个通道，即$Z=z_{1},\mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\boldsymbol{U} \boldsymbol{\Omega}^{1} \boldsymbol{U}^{\top} \boldsymbol{Z}$。那么，由K阶切比雪夫多项式近似的图形滤波器的参数矩阵$\Omega^1$被表述为

$$公式11:\begin{aligned} \mathcal{F}(\boldsymbol{A}, \boldsymbol{Z}) &=\sum_{k=0}^{K-1} \hat{\theta}_{k} T_{k}(\widetilde{\boldsymbol{L}}) \boldsymbol{Z} \\ \text { s.t. } & T_{k}(\widetilde{\boldsymbol{L}}) =2 \widetilde{\boldsymbol{L}} T_{k-1}(\widetilde{\boldsymbol{L}})-T_{k-2}(\widetilde{\boldsymbol{L}}) \end{aligned}$$

其中$\widetilde{\boldsymbol{L}}=2 \boldsymbol{L} / \lambda_{\max }-\boldsymbol{I}_{n}, T_{0}(\widetilde{\boldsymbol{L}})=\boldsymbol{I}_{N}, T_{1}(\widetilde{\boldsymbol{L}})=\widetilde{\boldsymbol{L}}$，$\hat{\theta}_k$表示置信度

亲和矩阵A受输入特征的影响，而不是使用固定的图结构。因此，所有可能的亲和矩阵的最大特征值存在一个上限，即$\lambda_{\max }=2$，当他们所有的图拉普拉斯L是归一化图拉普拉斯，有了这个假设，我们可以得到$\tilde{L}=-\boldsymbol{A}$，并将其带入公式11中。

$$公式12:\mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\theta_{0} \boldsymbol{Z}+\theta_{1} \boldsymbol{A} \boldsymbol{Z}+\sum_{k=2}^{K-1} \theta_{k} \boldsymbol{A}^{k} \boldsymbol{Z}$$

其中$\theta_k$可以通过GSD学习，然后将公式(11)拓展到多个通道，可以得到一个具有切比雪夫滤波的非局部算子的广义表述：

$$公式13:\mathcal{F}(\boldsymbol{A}, \boldsymbol{Z})=\boldsymbol{Z} \mathbf{W}_{1}+\boldsymbol{A} \boldsymbol{Z} \mathbf{W}_{2}+\sum^{K-1} \boldsymbol{A}^{k} \boldsymbol{Z} \mathbf{W}_{k+1}$$

其中$F(A,Z)$是非局部算子，$W_k \in \mathbb{R}^{C_s\times C_s}$是一个参数矩阵，请注意，当$C_{s} \neq C_{1}$时，可以直接将$W_{s2}和W_k$合并，这使得$\mathbf{W}_{k}=\mathbf{W}_{k} * \mathbf{W}_{s 2} \in \mathbb{R}^{C_{s} \times C_{1}}$。

公式13给出了nonlocal算子的空间观(spatial view)和光谱观(spectral view)之间的联系，其中图的过滤器是由第k个相邻的节点之间的聚合来表示的，因此，现有的基于非局域的结构可以通过公式13在光谱视图中进行理论分析。本文阐述了现有的5种可以统一的nonlocal blocks的类型。

1. NL blocks：光谱观(spectral view)中的NL块与定义图为$G=(V,D^{-1},M,Z)$，然后使用切比雪夫多项式的第二项来逼近广义图滤波器的做法相同。
2. NS module：光谱观中的NS模块被抗做是$G=(V,D^{-1}_M,M,Z)$形式的图，一阶切比雪夫多项式用于近似图滤波器，条件是$W_1=-W_2=-W_3$
3. $A^2$ blocks： 双重注意区块可以看作是图$G=(V,M,Z)$，然后我们可以使用切比雪夫多项式的第二项来近似图滤波器，即$F(A,Z)=MZW$
4. CGNL blocks：当把所有通道归为一组时，CGNL可以被看作是图$G=(V_f,D_{M^f}^{-1},M^{f},vec(Z))$，其中$V^f$包含空间位置和特征通道，同样，我们也可以使用切比雪夫多项式的第二项来逼近图形滤波器，即$F(A,Z) = D_M^{-1}M^fvec(Z)W$
5. CC blocks：在CC块中，$\mathcal{G}=\left(\mathbb{V}, \boldsymbol{D}_{\boldsymbol{C} \odot M}^{-1} \boldsymbol{C} \odot\right.M,X)$与掩码C，然后使用切比雪夫的第二项被用于近似滤波器的节点特征X。

设计光谱非区域块(Designing Spectral Nonlocal Blocks)

除了统一现有的非区域块，本文提出的"光谱观"(spectral view)也有助于设计具有理论保证的新型非区域块。作为一个例子，我们阐述了一个更合理的非区域块，成为光谱非区域块(Spectral Nonlocal Block,SNL)，它人谈基于切比雪夫滤波器，但具有更强的理论基础和稳健性。

基于以上部分，现有的基于非局部的算子使用随机行走归一化(random walk normalized)（NL,NS,CGNL,CC）或非归一化的亲和矩阵$A^2$。对称性是没有保证的，其性能取决于亲和力核。这导致图谱频域的不存在，并导致图拉普拉斯的大量复杂特征值，这个问题在非局部区块的全连接图模型下会被放大。

现有的非本地块只使用第二项(NL,A2,CGNL,CC)或具有共享权重的一阶近似(NS)，而不是完整的一阶近似，这也阻碍了其性能。因此，考虑到这些因素，拟议的SNL块应用了一个对称的亲和矩阵，具有更完整的近似值如公式14所示

$$公式14:\begin{aligned} &\boldsymbol{Y}=\boldsymbol{X}+\mathcal{F}_{s}(\boldsymbol{A}, \boldsymbol{Z})=\boldsymbol{X}+\boldsymbol{Z} \mathbf{W}_{1}+\boldsymbol{A} \boldsymbol{Z} \mathbf{W}_{2} \\ &\text { s.t. } \quad \boldsymbol{A}=\boldsymbol{D}_{\hat{M}}^{-\frac{1}{2}} \hat{\boldsymbol{M}} \boldsymbol{D}_{\hat{M}}^{-\frac{1}{2}}, \quad \hat{\boldsymbol{M}}=\left(\boldsymbol{M}+\boldsymbol{M}^{\top}\right) / 2 \end{aligned}$$

其中$F_s(A,Z)$是SNL操作，$W_1,W_2$是双参数矩阵

拟议的SNL使用切比雪夫滤波器作为广义的图滤波器，但有一个更彻底的平方，由本文提出的光谱观进行分析。具体来说，他使用对称的亲和矩阵$\boldsymbol{A}=\boldsymbol{D}_{\hat{M}}^{-\frac{1}{2}} \hat{\boldsymbol{M}} \boldsymbol{D}_{\hat{M}}^{-\frac{1}{2}} t$来确保实数特征值的存在，这使得他在插入到深度神经网络时更加稳定，此外，拟议的SNL还使用了一阶切比雪夫近似法的完整形式，这是一种更精确的图式滤波器的近似。因此，他可以给出的异步学习空间，只需要多一个参数矩阵。

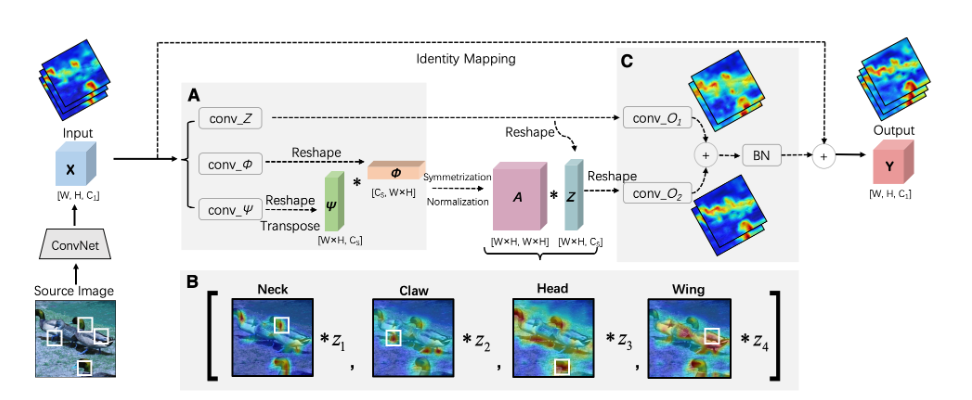
SNL(Spectral Nonlocal Block)实现的细节图

输入特征图$X \in \mathbb{R}^{W\times H\times C_1}$首先被送入三个1x1的卷积与权重核$\mathbf{W}_{\phi, \psi, g} \in \mathbb{R}^{C_{1} \times C_{s}}$以减去通道数，然后被重塑为$\mathbb{R}^{ WH \times C_{s}}$。其中一个输出$Z \in \mathbb{R}^{ WH \times C_{s}}$被用作转移的特征图，以减少计算的复杂性，而另外两个输出$\boldsymbol{\Phi}, \boldsymbol{\Psi} \in \mathbb{R}^{W H \times C_{s}}$被用来得到具有亲和核函数$f(\cdot)$的亲和矩阵A。然后，A被制成对称的，并按公式14进行归一化，最后，利用亲和矩阵A和转移的特征图Z，非局部区块的输出可由公式14得到，具体来说，两个权重矩阵$W_1,W_2 \in \mathbb{R}^{C_s \times C_1}$是由两个1x1的卷积产生的。