「分割汇总」百度七日分割学习记录(一)
百度分割学习(一)
语义分割算法的基本概念
语义分割算法的基本流程
- 输入:图像(RGB)
- 算法:深度学习模型
- 输出:分类结果(与输入大小一致的单通道图)
- 训练过程
- 输入:
image+label - 前向:
out = model(image) - 计算损失:
loss = loss_func(out,label) - 反向:
loss.backward() - 更新权重:
optimizer.minimize(loss)
- 输入:
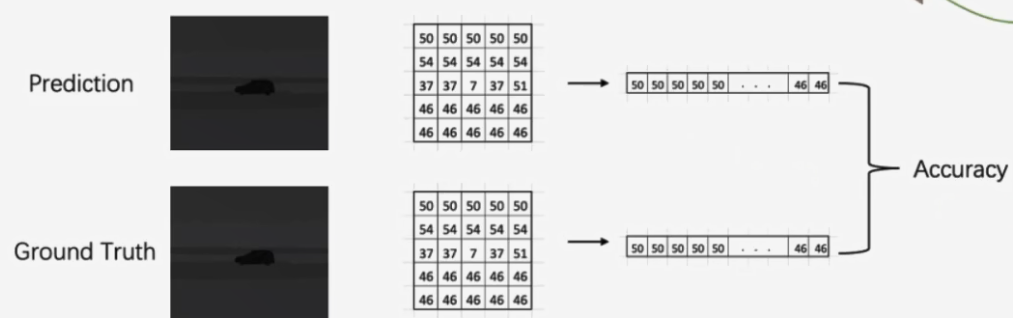
分割网络的性能指标mAcc
将pred矩阵和GT矩阵打平然后比较每一个数字是否相同,这里的数字表示的这个位置的像素点应该是什么标签,这里的数字就是标签,两个标签相同才正确
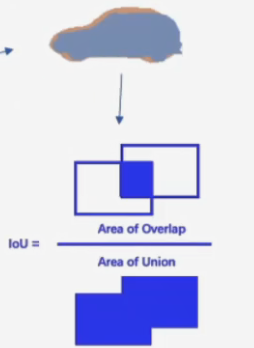
语义分割性能指标mIoU
分割每一个类别的交并比
mean主要体现在求了每一个类别的交并比后取均值表示为最终结果
全卷积FCN网络
FCN全称是Fully Convolusional Networks,通俗地讲就是全卷积,没有FC层
Feature map尺寸变大:
卷积:卷积越卷越小
upsample(上采样):越变越大
-
Up-sample
1. 上采样方法:Bilinear Interpolation(双线性插值法)- 在paddle中的函数是
fluid.layers.interpolate(data,out_shape=(),align_corners=True)- out_shape输入的是图片的长宽,最后一个参数是默认True
-
Transpose conv
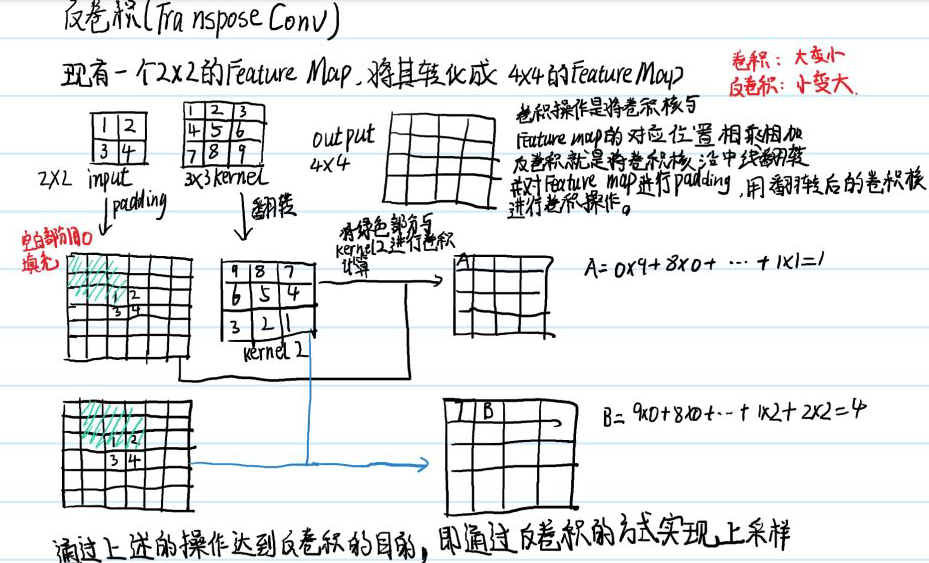
-
padding值的确定,是根据他的卷积核决定的,就是说你的pooling之后,还原左上角的数字时,要求padding后的feature map的左上角与卷积核重叠后,正好只有padding前的左上角
-
这个反卷积的函数是:
fluid.dygraph.Conv2DTranspose(num_channels,num_filters,filter_size,stride)-
num_channels是输入的通道数
-
num_filters是输出的通道数(卷积核的个数)
-
filter_size是卷积核的大小
-
stride是步长
-
-
Un-pooling
-
池化层函数使用:
paddle.fluid.dygraph.Pool2D(pool_size=2,pool_stride=2,ceil_model=True)- 参数pool_size是要池化的倍数
- pool_stride是移动的步长
- ceil_model是面对不同尺寸的输入时的一个取整
-
在
Conv2D中加入一个参数act = 'relu'可以在卷积层结束后执行relu激活 -
创新点分析:在FCN中使用的是传统的VGG结构,但是在最后的两个全连接层中,使用1x1卷积的方式进行替换,提高了计算的效率,同时使用上采样额方式将feature map还原图尺寸,然后实现像素级分类
UNet网络结构
视频上的图太糊了,我换一个
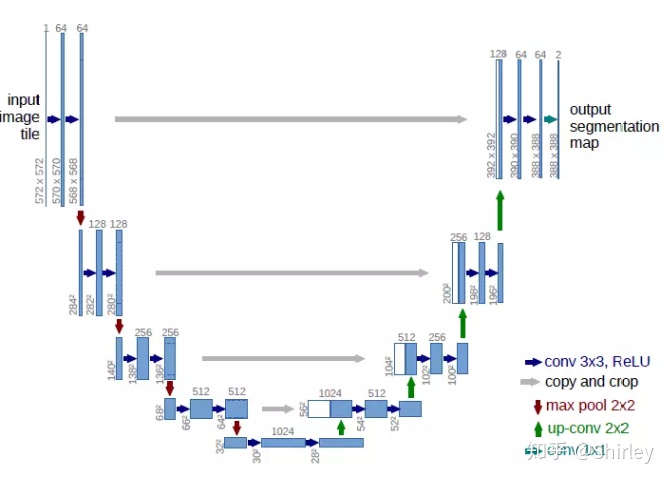
从图中可以看出Unet的网络结构就是一个U字形的架构
他分为左中右三个部分
网络结构解读
-
先看左边的部分,在第一行中先使用两次卷积提取出特征,存储这次卷积后的feature map我们称这个feature map为pool1
-
进行一个最大池化的操作,获得新的结果
-
在第二行中,将新的结果再进行两次卷积提取出特征,再存储这次卷积后得到的feature map我们称这个feature map为pool2
-
再进行一个最大池化的操作,获得新的结果
-
在第三行中,将新的结果进行两次卷积提取出特征,再存储这次卷积得到的feature map,我们称这个feature map为pool3
-
再进行一个最大池化的操作,获得新的结果
-
在第四行中,将新的结果进行两次卷积提取出特征,再存储这次卷积得到的feature map,我们称这个feature map为pool4
-
这样网络的左边部分解结束了,左边部分的实际结果是增加了通道数,缩小了尺寸
-
在中间部分,仍然是两个卷积,但是卷积只增加了通道数没有进行尺寸的改变,使用的是1x1的卷积,获得结果mid
-
然后到右边部分第四行,经过前两个过程的mid会进行一个上采样的工作,接着就是将mid和pool4进行一个堆叠的操作,这时候mid的通道数就会变成原来的两倍,然后使用两个卷积层对这个mid进行通道缩小
-
到右边第三行也是一样的操作,直到右边第一行,我们的feature map在与pool1融合后,继续进行一个卷积的降维的操作,使其通道数,变成我们分类数目,在使用softmax对这些进行分类就结束了
创新点分析:采用了各层特征堆叠的方式,增加获取到的图片特征信息
PSP分割网络
psp分割网络:Pyramid Scene Parsing Network
FCN的缺点:
- 分割结果不够精细
- 没有考虑上下文信息
PSP网络能通过扩大感受野(Receptive Field)来获取上下文信息
什么是感受野(RF):
- 感受野 = 用于产生特征的输入图像中的区域大小
- 只针对于局部操作:比如conv,pooling
PSP网络的Pyramid Pooling模块
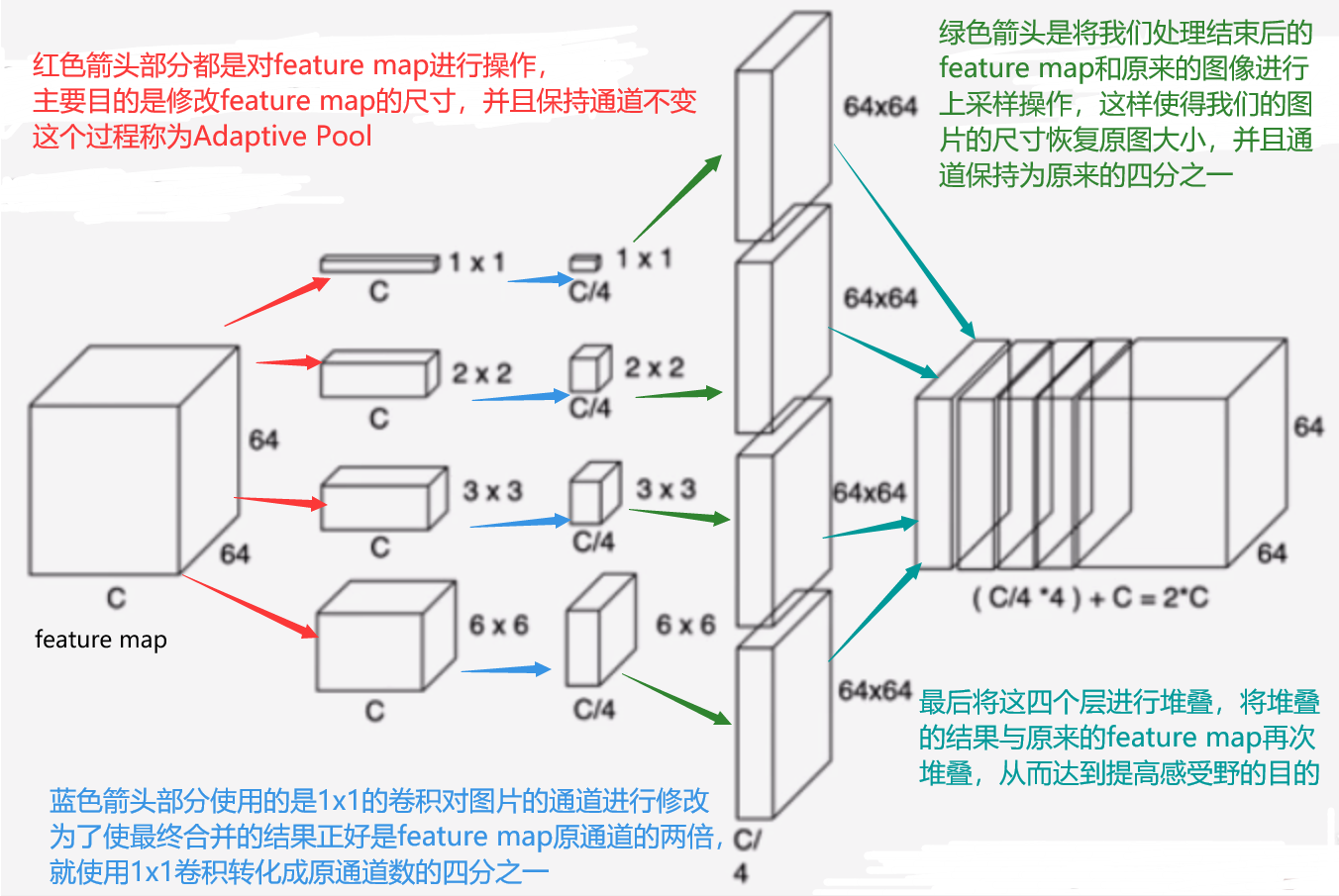
这个psp模型Pyamid pooling模块在YOLOv4中也有应用过
PSP的整体结构
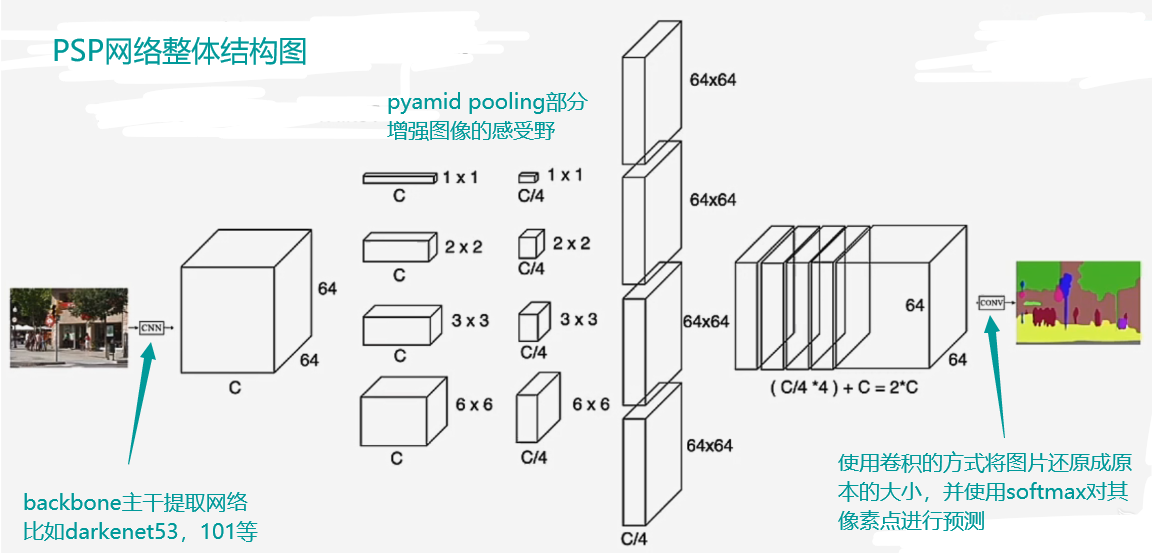
创新点分析:通过卷积的方式将feature map转化成各个尺寸的feature map,再通过上采样还原成原图尺寸,再将这些feature map与原feature map进行堆叠,从而达到扩大感受野的目的
空洞卷积(Dilated Convolution)
- Dilated conv:
- 理解1:将卷积核扩大,扩大的部分填0
- 理解2:feature map 间隔计算conv
- 空洞卷积模式图:
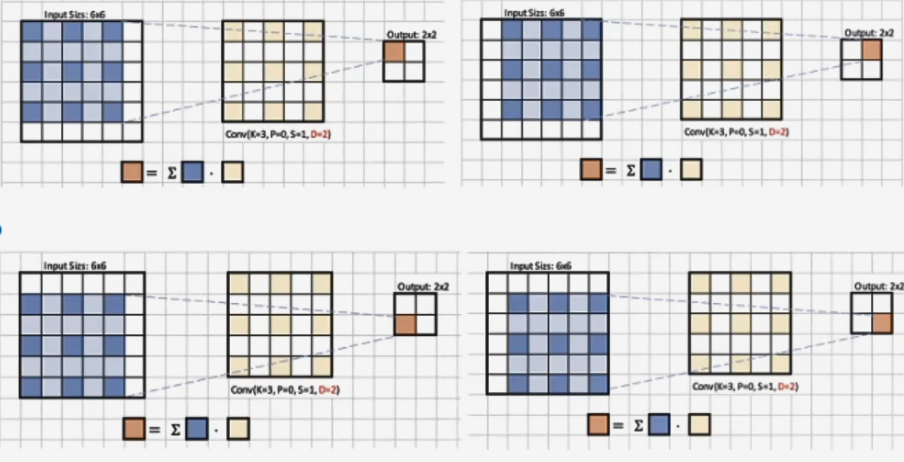
从图中可以看出,我们原本的3x3的卷积核变成5x5的卷积核,3x3卷积核的数值分散到上下左右。四个角和中间部分,其他部分用0来填充,完成新的空洞卷积核
虽然用新的方式构造了这样一个东西,但是本质还是一个卷积核,执行的仍然是卷积操作
- 空洞卷积的输出计算公式:
p是padding
D是卷积核中两个像素点的距离+1
k是原来卷积核的大小
S是卷积核移动的步长
- PSP分割网络的-Backbone(主干提取网络):
- 在传统的ResNet使用的是Dilation为1的卷积即无空洞的卷积
- 在Dilated ResNet(空洞的ResNet)中第四层和第五层使用的是Dilation为2和4的卷积核
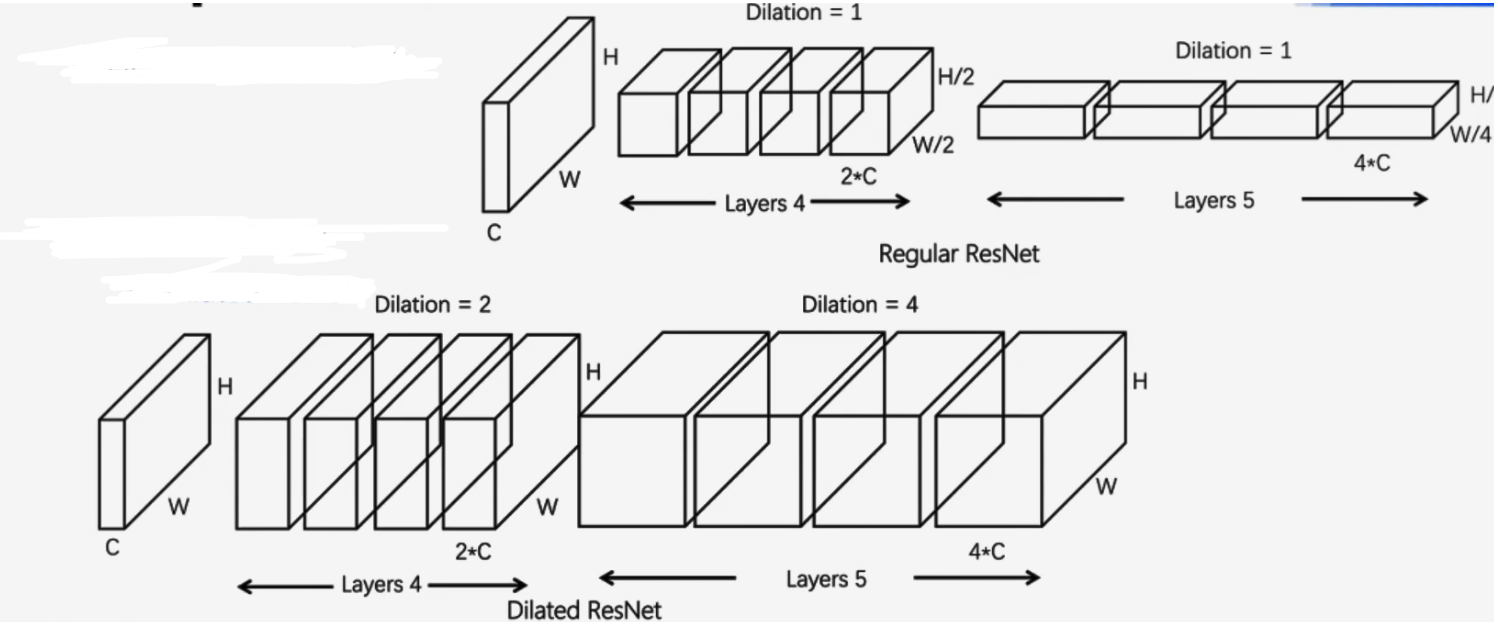
从图中可以看出,空洞的ResNet(下)的变宽都是和原本的feature map的宽高是相同的,同时他的channel也是有一定的增加。对比与·传统的ResNet(上),从结果上看,扩大后的感受野就会增大。
个人看法:
这个空洞卷积使得,在进行卷积操作时将像素点离散化,获取更多的上下文信息,这个就是说,将使用一个较大的卷积核,去提取图片的特征,但是,并不是提取出全部的内容,只采采取几个部分的点,使得新的feature map获得是离散化的信息,而不是连续性的信息。
这个空洞卷积的使用仍然是,Conv2D,只是多添加了一个Dilation的参数,不另外多加一个API
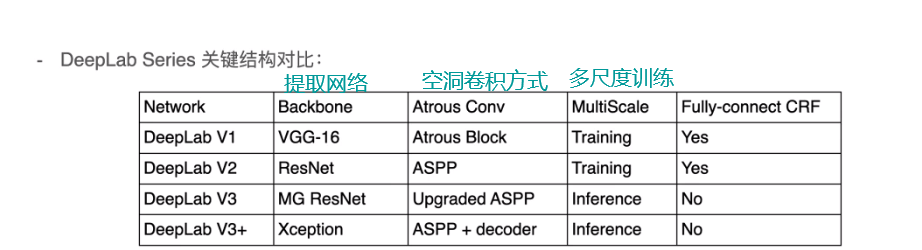
DeepLab系列网络
- v1~v3+的论文名称
- V1: Semantic image segmentation with deep convolutional nets andfully connected CRFs (ICLR 2015)
- V2: DeepLab: Semantic lmage Segmentation with Deep Convolutional Nets,Atrous Convolution, and Fully Connected CRFs(TPAMI 2018)
- V3: Rethinking Atrous Convolution for Semantic lmage Segmentation
- V3+: Encoder-Decoder with Atrous Separable Convolution for Semantic lmage Segmentation (ECCV 2018)
- 四个版本的结构对比
多尺度训练和CRF中的使用从V3开始就不使用了,应该是发现了后面这两个东西的影响不大。
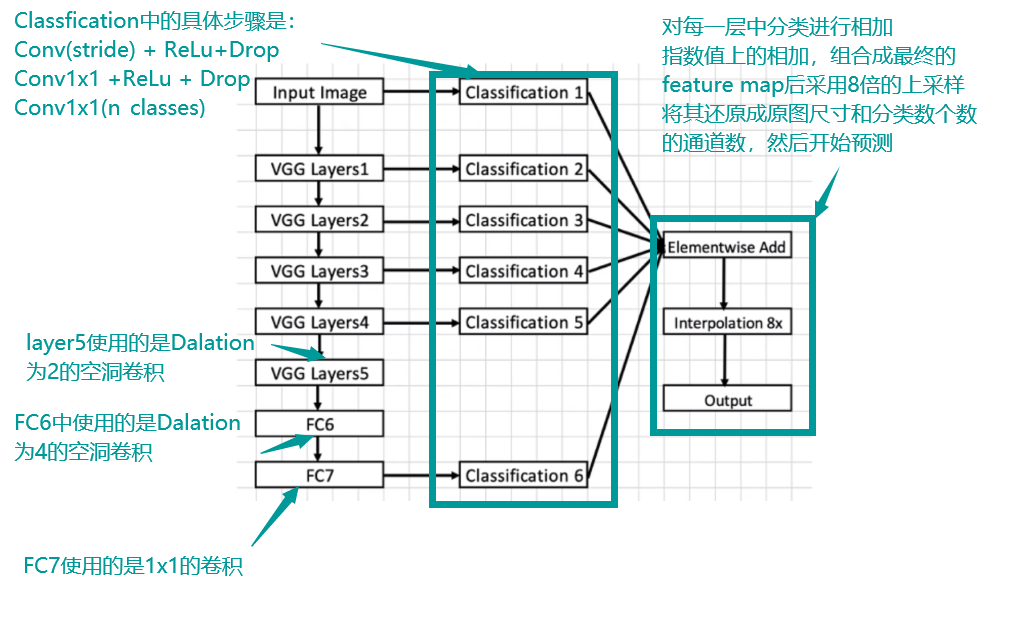
- DeepLab V1 网络结构的解析:
-
在VGG的结构中,下采样基本是使用pooling的方式,而不是直接使用conv,这会致使classfication1~6的feature map宽高可能会不相同,因此在classification中有一个Conv(stride)这个的目的是通过控制步长来让卷积后的feature map变成我们希望的尺寸大小
-
同时还应该注意的是Layer5和Layer4,以为从Layer5的时候使用的是空洞卷积的方式来扩大感受野,因此Layer5和Layer4中需要设置pooling的参数(k=3,s=1,p=1)使得我们再下采样后保持原来的尺寸
-
创新点应该是嵌入了空洞卷积的提取网络和对指定层分类结果的融合
-
DeepLabV2网络结构解析
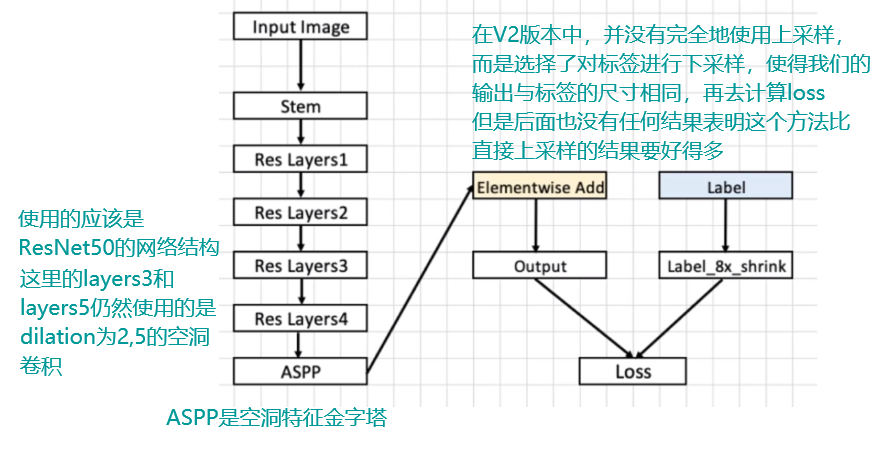
- 这里的stem结构课上没有讲到,论文里应该有,我先百度了一下,据说是通过这个结构获得尺寸缩小n倍的特征图
- ASPP的结构
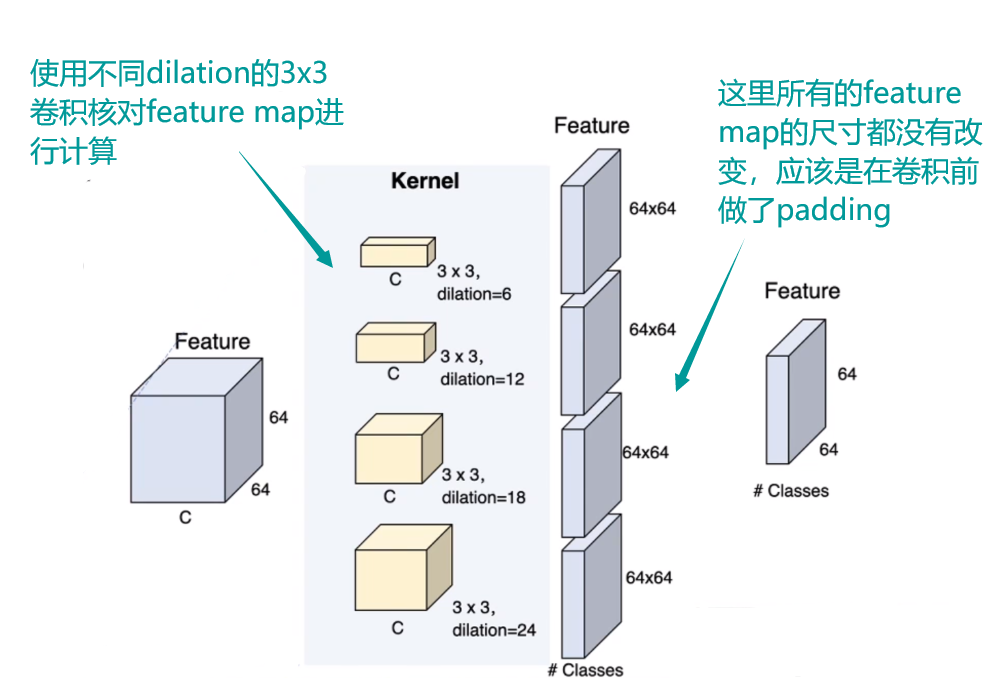
- 在进行空洞卷积的过程中,dilation的值作为padding的值就能保证feature map的尺寸相同
- 举个例子(输入的宽高为64x64,s为1,卷积核为3x3):按照之前说的空洞卷积公式
- 对于普通的卷积他的dnation是1:那么他是的padding也是1,计算一下
- 对于空洞卷积,假设dination是6,那么他的padding也是6,计算一下:
-
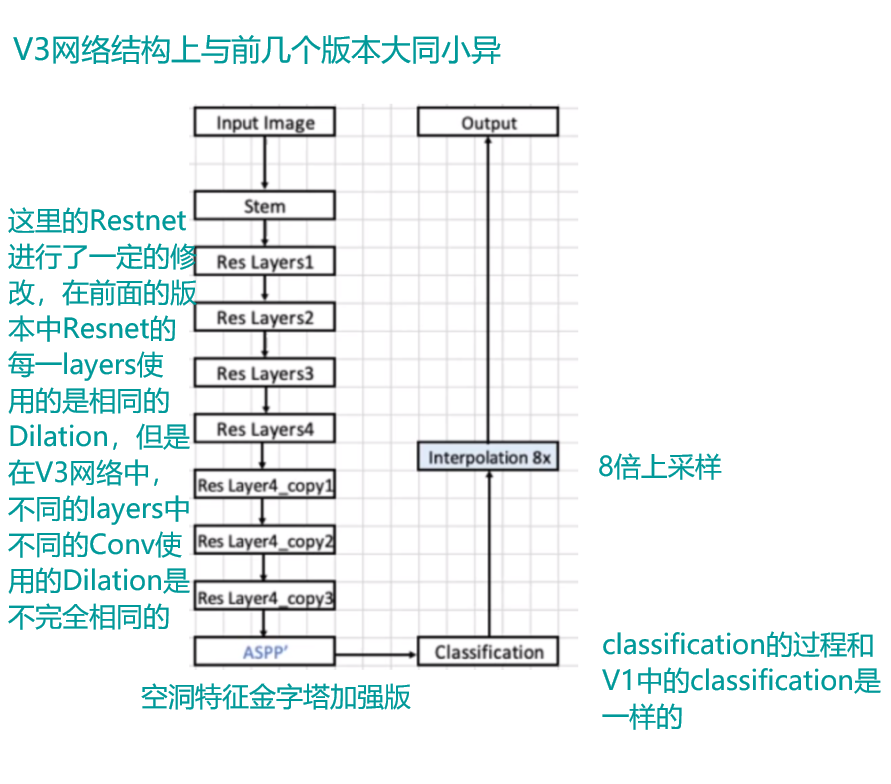
deeplabV3
- ASPP加强版:
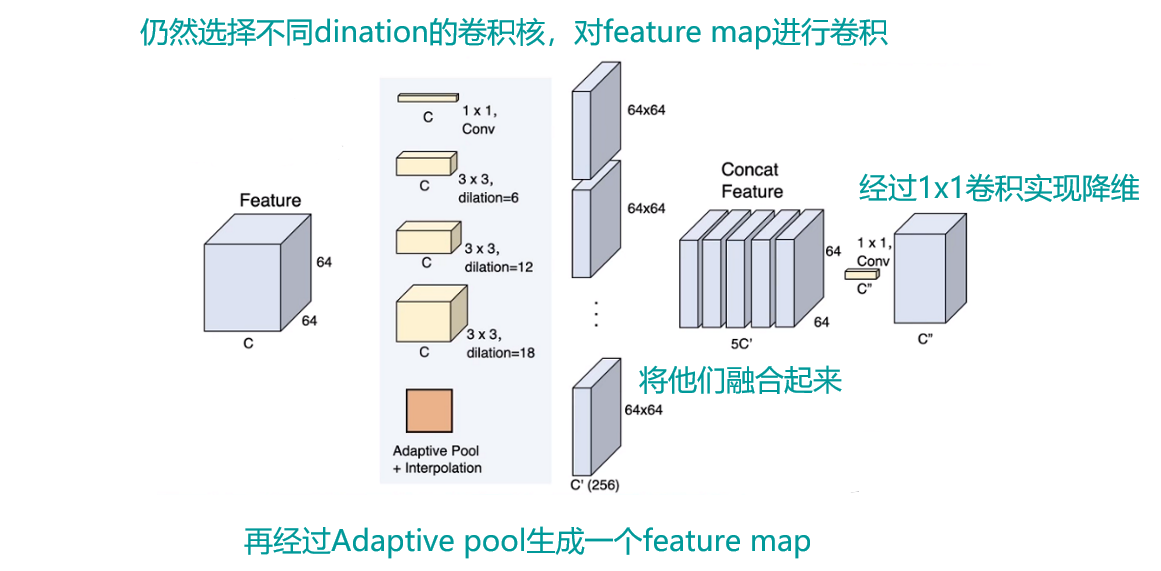
- 整体网络结构
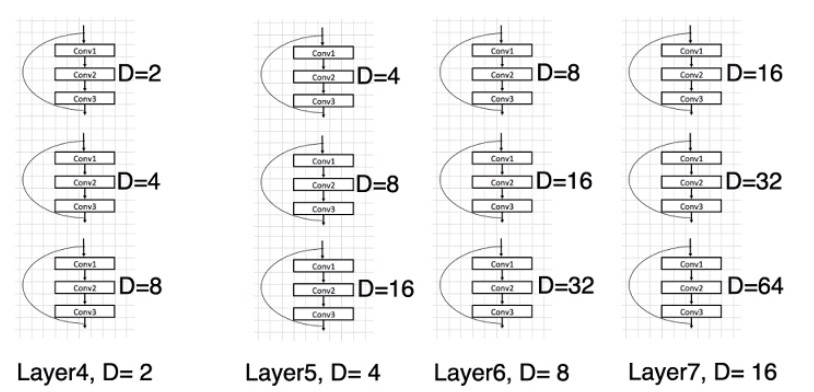
- 后面几层使用的Dilation值:
- ASPP加强版:
图卷积
令人迷惑的图卷积
-
图卷积公式
提出图卷积的论文:
Thomas N.Kipf and Max Welling, Semi-Supervised Classification with Graph Convolutional Networks,ICLR 2017
可以将图卷积公式变形为
L是消息传递网络(Message Aggregation Network)W是状态更新网络,可以通过不断学习从而进行优化
-
上下文的基本概念:
- 什么是上下文:
- 物体的空间依赖(人类的眼睛在眉毛的下面)
- 语义类别依赖(水上的交通工具是船而不是车)
- 场景先验(厨房中会出现常用的厨具而不会是电子产品)
- 如何建模?
- 全局特征统计(BoW,VLAD,Fisher Vector)
- 条件随机场,非局部神经网络
- 基于区域的图推理
- 什么是上下文:
Beyond Grids: Learning Graph Representations for Visual Recognition(超越网格:学习图表示的视觉识别)
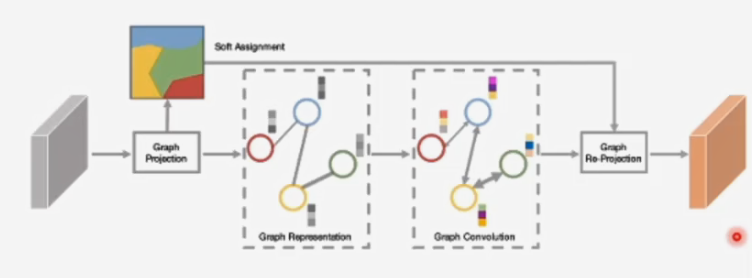
- 堆叠卷积核池化操作的深度模型存在的问题:
- 有效感受野非常有限
- 不能很好地进行上下文建模
- Graph Convolutional Unit(GCU)学习图的组成
- Graph Pojection :投影2维的特征图X成图,通过聚类的方式将相似的特征进行聚类,聚类中金就是节点表征
- Graph Convolution :在图g上执行图卷积(沿着图上的边进行特征传播,建模全局上下文),得到新的图表特征
- Graph Re-projection :将新的图表征反投影到2维空间,使得整个GCU能够即插即用
- 计算方式:
- 图投影(Graph Pojection):首先是将一个(W,H,C)的一个feature map,reshape成(WxH,C)的一个二维矩阵,
- 接着计算他的分配矩阵,V指的是图的节点数目
- 计算方式为
- 先计算像素与第k个节点(聚类中心)的距离,然后再对其进行归一化处理
- 这里的和都是可学习的参数,
- 这里的指的是我们feature map上的像素在第k个节点上的权重有多大
- 计算图表征
- 先计算出像素与聚类中心的距离,然后乘上权重做归一化处理,从而构成图表征
- 计算邻接矩阵,计算的是两个节点间的相似程度,和图论中的邻接矩阵不太一样
- 图卷积(Graph Convolution):
- 图卷积就是用我们的邻接矩阵乘上我们的图表征的转置,再乘以一个可学习的参数
- 图反投影(Graph Reprojection):
- 图投影(Graph Pojection):首先是将一个(W,H,C)的一个feature map,reshape成(WxH,C)的一个二维矩阵,
Graph-Based Global Reasoning Networks(基于图的全局推理网络)
- 研究动机:
- 当前卷积神经网络不能够有效建模相距较远的区域之间的全局关系
- 解决思路
- 提出一种新的全局推理方法,将坐标空间(Coordinate Space)的像素级特征聚合投影到交互的空间(Interation Space),然后进行有效的关系推理,最后将具有关系属性的特征反投影回原始的坐标空间
- 将一个图像中的信息进行聚类,然后将聚类后的的特征聚类中心作为图的一个节点,然后投影到交互空间中进行推理,经过推理后的内容信息,经过反投影回到原来的二维图像,实现堆内容特征的信息增强,图中节点数确认方式不是说有多少个类别就选择多少个戒节点,而是说他们节点数的确认方式是经过一些机构多次试验后得出的结论。
- 具体方式
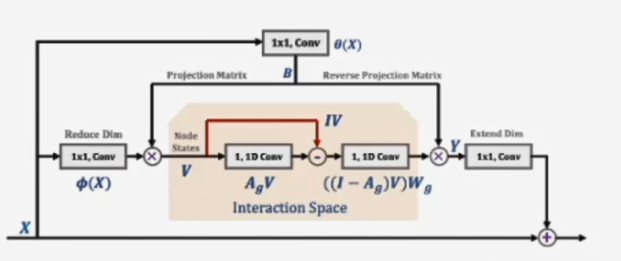
- 提出Global Reasonling(GloRe) unit,其通过加权全局池化来实现coordinate-interaction space的映射,并且通过图卷积在交互空间进行关系推理
- 从坐标空间到交互空间(建图):
- 将输入的feature map转化成维度为[HxW,C]的这样一个空间矩阵,然后将其映射为交互空间的表征V = f(X)
- f函数的设计,通过网络去生成这样一个f函数,其实这个函数也不难就是,生成一个矩阵与我们的X进行相乘,这个矩阵是一个可学习的矩阵
- 用B矩阵的一行,对X中的每一行进行相乘然后相加,作为V的一个值
- 可学习矩阵
- 图卷积进行推理:建模任意区域之间的关系转化为学习交互空间中节点的交互
- 表示的是邻接矩阵,V表示我们特征图的投影信息(图表征),是一个可学习的参数
- 图卷积是每一个节点之间的信息交互,在这里采用的是用1x1卷积的方式来模拟这个过程
- 从交互空间到坐标空间(反投影):将新的图表征反投影到坐标空间,使得整个GloRe能够即插即用
GINet: Graph Ilnteraction Network for Scene Parsing
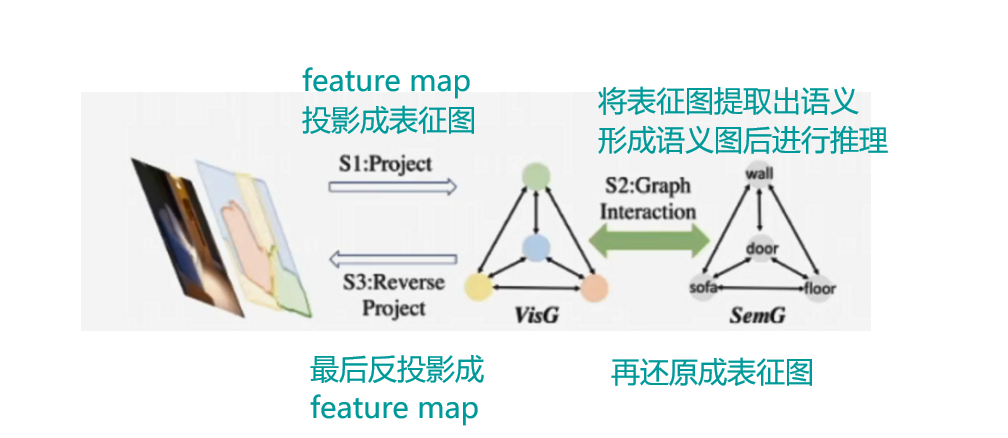
- 主体构造与结构解析
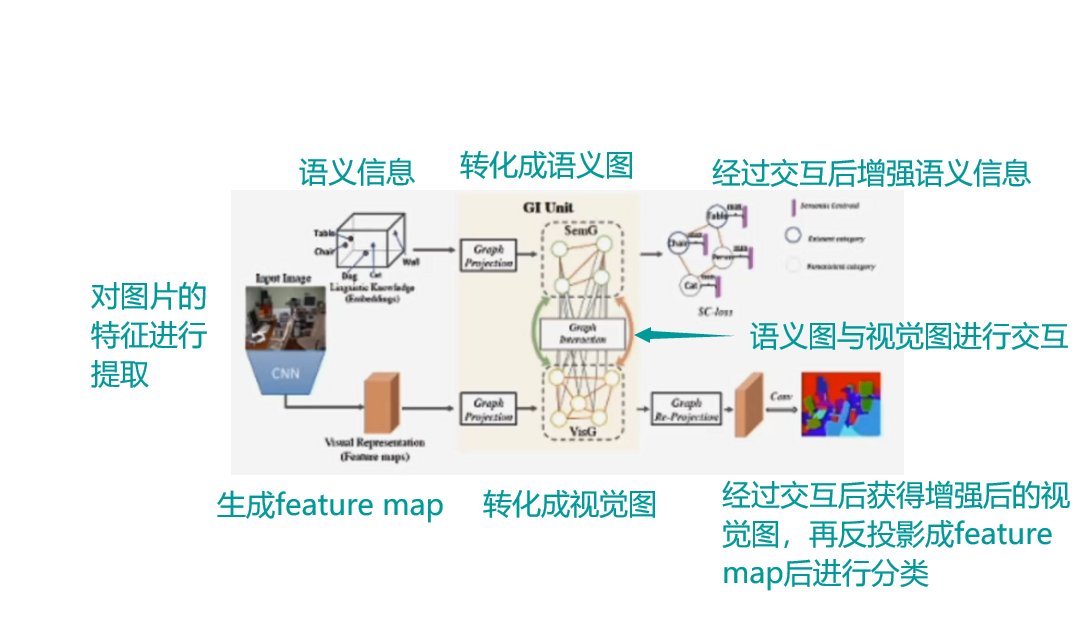
- 具体方法:
- 图的构建:
- 视觉图构建方法:P = ZXW
- P是视觉图,,N是样本数,D是视觉图中节点个数
- 映射视觉特征
- 是投影矩阵
- 是特征维度变换矩阵
- 语义图S构建方法:
- 是每个类别的语义特征
- 语义到数据推理:每个数据图的节点表征提取对应语义表示为:
- 是可学习向量
- 是分配矩阵
- 是可训练参数
- 视觉到语义推理:给每个输入样本生成基于样本的语义图表征
- 是可学习变量
- 是分配矩阵
- 是可训练参数
- 单元输出:将新的视觉图表征投影回二维的像素级特征:
- 图的构建:





