「论文阅读」Learning Temporal-Correlated and Channel-Decorrelated Siamese Networks for Visual Tracking
Learning Temporal-Correlated and Channel-Decorrelated Siamese Networks for Visual Tracking
论文名称:Learning Temporal-Correlated and Channel-Decorrelated Siamese Networks for Visual Tracking
作者:Mao Xi; Wengang Zhou; Ning Wang; Houqiang Li
期刊:IEEE Transactions on Multimedia
时间:2021-6-08
原文摘要
Recently, Siamese network based trackers have attracted growing popularity in visual tracking, which tackle the
tracking by template matching between the initial template and successive search regions. The initial template patch is generally encoded into a convolutional feature for matching. However, the limited representational capability of the template feature limits the tracking accuracy. Besides, thisfixed representation also fails to adapt to the target appearance changes. To alleviate these issues, we improve the Siamese trackers by introducing temporal correlation and channel decorrelation mechanisms. On the one hand, we consider the channel-wise correlations between the initial and historical template features to adaptively aggregate informative channel-wise representations for template update. On the other hand, we propose a decorrelation regularization to weaken the channel-wise correlations of individual template features. By end-to-end training, we learn a more complete and adaptive template for accurate object tracking. We demonstrate the generality of our approach by applying it to two prevalent Siamese trackers, i.e., SiamFC and SiamRPN. Extensive experiments on seven benchmark datasets verify the effectiveness of our method.
摘要
基于Siamese network(暹罗网络,连体网络)的追踪器在视觉跟踪领域引起了越来越多的关注。他通过在初始的模板和连续搜索区域之间的模板匹配实现追踪任务。初始的模板块通常被编码成卷积特征用于匹配,然而模板特征有限的表征能力限制了追踪的精确度。并且,这种固定的表示方式无法适应目标外观的变化。为了缓解这个问题,作者通过引入时间相关(temporal correlation)和通道去相关(channel decorrelation)的机制改进了Siamese 追踪器。一方面,可以考虑初始模板和历史模板特征的通道相关性,以自适应地聚合用于模板更新信息的通道表征。另一方面,作者提出了一个去**相关正则化(decorrelation regularization)**去弱化每一个独立模板特征的通道相关性。通过端到端的训练,学习到了一个更加完整和自适应的模板来进行精准的目标跟踪。作者通过将其应用于两个流行的Siamese跟踪器SiamFC和SiamRPN来展示该方法的通用性。在七个基准的数据集上进行大量的实验来验证这个方法的有效性。
Introduction
传统的视觉最总的目标是使用优先的先验知识(通常是第一帧的注释)去估计目标在视频中的位置。
因为一些non-trivial的因素如快速移动,遮挡,变形,光照变化等,视觉追踪任务仍然是一个有挑战的任务。
根据模型是否要更新可以将视觉跟踪分为两组方法。
第一组利用第一帧去初始化模型,并增强地在线更新模型以区分背景和目标。即使地在线更新缓解了由目标外观变化造成的偏移(drift)问题,但这需要更多的计算开销。
作为在线更新模型的替代,第二组关注于模板和搜索区域之间的模板匹配和相似图的计算。作为第二组方法的代表,Siamese-base的跟踪器在第一帧初始化目标模板,并在后来的帧中保持模板的固定,这比在线更新的方法更加有效率。
在Siamese跟踪器中,模板块由卷积特征表示,并与搜索区域中的深度特征进行卷积实现匹配。然而,固定的模板特征不仅使得自适应目标外观变化失败,还受限于优先的表示能力。
于是作者的目标是通过时间相关性和通道去相关性来增强模板表示能力,实现更加有效的Siamese跟踪器。如图1所示,作者提出的方法不仅考虑了不同通道在每一个模板特征上的相关性,还考虑了初始特征和历史特征的通道相关性。
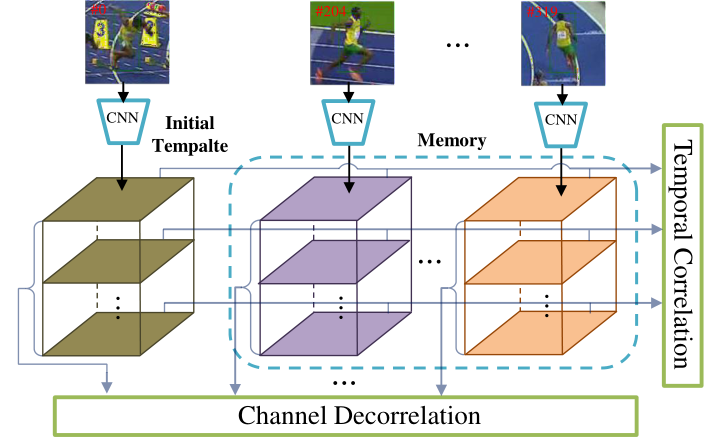
图1
Channel Decorrelation的目的是弱化每一个独立特征的通道相关性,以学习更完整的表示
temporal corelation计算内存中的初始模板和历史模板之间的通道相关性,然后将有价值的通道表征集成到初始模板中进行细化。
作者提出了时间相关性机制去自适应的更新初始模板特征,具体来说,作者测量了初始模板特征和历史模板特征的通道相关性,然后动态地聚合历史模板特征的通道表征到初始模板中。与平均移动方法实现的直接特征聚合相比,作者不计算global-level的特征相似度,这使得每个特征通道被公平对待,并忽视了不同视觉模式的不同重要性。
因为现代深度卷积网络遭受来自训练数据不充分的高冗余和过拟合的影响。作者在训练阶段引入了一种去相关性正则化的损失函数(decorrelation regularization loss),去弱化不同通道之间的相关性,这能有效减少卷积核的冗余,并带来具有卓越表示能力的更全面的模板特征。此外,通道切相关性正则化有利于之前提到的时间相关性的估计。
作者提出的方法仅仅引入了两个额外的FC层,这带来了额外的计算负担,但仍然保持了Siamese网络的高效率跟踪。
本文的主要贡献
- 提出一种时间相关性机制通过聚合历史内存表征去自适应地更新初始模板特征。同时,引入通道去相关性正则化去减少模板通道的相关性,这鼓励每个通道去表达特定的特征,使模板功能更加多样和完整。此外,包括上述两个组件在内的整个架构都进行了端到端的优化。
- 作者将这两个方法融入到了两个主流的Siamese追踪器SiamFC和SiamRPN中,对起个标准的跟踪数据集进行了广泛的实验如OTB2015, VOT2016, VOT2018, UAV123, TempleColor,TrackingNet, LaSOT。本文的方法持续改进了Siamese追踪器,同时保持其实时效率。
本人看法:
文章一直在突出,自己的工作是在针对固定的模板特征无法适应目标外观改变,这是一个重要的写作方式,避免读者或审稿人在进行文章阅读时,遗忘了文章要解决的问题。
SiamFC:全卷积的Siamese网络,他通过搜索区域上的空间相关来搜索目标
SiamRPN:通过引入RPN模块对SiamFC进行拓展,该模块直接回归目标边界框而不是传统的多尺度估计。
追踪模型更新的方法:基于相关性的追踪,基于梯度下降的追踪,Siamese更新的追踪
Proposed Method
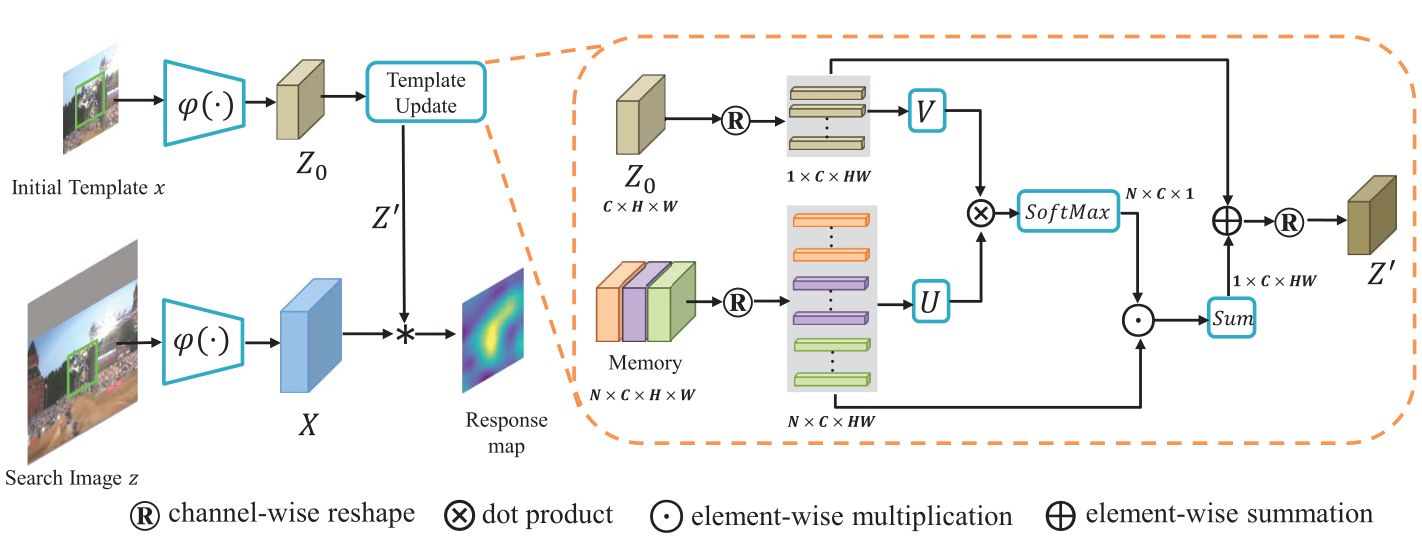
图2
上层的分支提取出初始模板的卷积特征,然后利用内存中的卷积特征进一步细化,生成一个新的模板特征。
内存中保存了历史模板的特征,并将在在线跟踪时进行跟新,U和V是线性转化模块。
图2展示了使用了时间相关性模板更新机制的Siamese跟踪框架。上层分支提取初始特征,在通道上使用历史模板特征的方法进一步获取时间相关性,去生成精细化的模板特征。将动态细化的模板特征和搜索区域的特征进行卷积生成响应图(response map)。
个人想法:由于对追踪任务不太熟悉,在第一次听到跟踪任务时想过,如果是追踪的话时序关系应该是比较重要的,那么如果能够用某种办法将之前的帧与当前帧进行集合,会不会能够给模型带来提升。这个想法与作者的思路有一点相似,但我觉得这个想法应该是大家都这么认为的,作者厉害的地方在于,他能够在时间相关性的基础上,将特征图通道进行去相关性,这使得每个特征图都可以由自己的重要功能。这是我所想不到的。
Revisiting Siamese Tracker
Siamese跟踪器采用双流结构,其中一个分支学习目标patch的特征嵌入,另一个分支学习搜索图像的特征表示。这两个分支在CNN特征提取器上实现参数共享,这样两个patches就可以通过相同的转换进行隐式编码。然后跟踪相似图由模板和搜索特征之间空间互相关生成。本文将和分别表示初始模板块和搜索块的输出特征图。相似度分数图可以用公式1计算
其中表示互相关(cross-correlation)操作,是相似度的偏移量。
通过在线跟踪中引入时间相关性更新和在训练过程中引入通道去相关正则化损失,提高了Siamese跟踪器的鲁棒性。为了验证这个方法的有效性和通用性,本文选择了两个主流的Siamese跟踪器
-
SiamFC 是第一个方法去利用全卷积网络通过逻辑损失训练网络实现视觉跟踪。逻辑损失可以用公式2表示
其中y表示ground-turth标签,g表示输出的真实分数。有这个框架易于实现,并且在准确性和速度上取得了很好的平衡,SiamFC已经成为了许多后面的跟踪器的baseline
-
SiamRPN将目标位置的分类损失和目标尺度的回归损失结合,引入了RPN模块对网络进行训练。SiamRPN不仅可以精确回归目标尺度,并且有着比SiamFC更快的跟踪速度。因此,这个框架今年来也非常受欢迎。
Temporal Correlation for Template Update
在传统的Siamese跟踪器中,上层分支值需要使用初始帧计算一次来提取模板特征。在本文的方法中,在连续帧可以得到的情况下,利用先前的跟踪结果,通过通道的时间相关性对初始化模板特征进行细化。时间相关性模板更新的细节被显示在图2中的橙色实线框中。
模板更新
为了清晰地演示更新过程,本文将表示内存(memory)中的特征集合。初值状态下N的值为0,然后将满足添加的历史模板特征加入到内存中。时间上,考虑到有限的内存和计算资源,本文设置内存容量的最大值为。和分别表示初始化模板的剪辑特征和历史预测跟踪结果。为了得到模板更新,首先,初始化模板特征和在内存中的历史模板特征被根据通道维度打平,从变为。和分别表示和第j个通道的拓展向量。比如,和的尺寸在SiamFC中为,此外,和的向量维度为36。然后计算和之间相关性可以用公式3表示
其中表示两个向量的点积。和是由一个全连接层实现的线性转化模块。表示初始模板和第i个内存中的模板特征在第j个通道上的相似度。给定N个内存中的历史模板,对内存中的N维特征使用损失函数计算出归一化权重,计算方式为
在得到每个的通道重要性后,通过使用权重,聚合历史通道表征,其可用公式5表示
其中表示第J个使用内存模板聚合的通道特征。
使用上述的方法单独聚合每一个通道特征。之后,在通道维度上拼接多个去的得到形状为的。然后,通过直接像素相加(element-wise summation)的方式实现了融合和在通道上打平的。最后将结果从转化为得到更新后的模板。如图2中所示。在在线追踪过程中,虽然网络参数保持不变,但当新的历史模板特征添加到内存中时,模板特征的权重将不断变化。此外,根据初始帧的运算,将预测的目标patch固定为的大小。因此,预测的模板特征的分辨率与初始模板特征的分辨率相同。获得更新后的模板后,SiamFC的输出结果可以由和搜索区域的特征的互相关性计算出来。在SiamPRN中,将进一步通过RPN模块获得目标的位置和大小。
内存更新
本文广泛使用了Peak to Sidelobe Ratio(PSR)来评估跟踪的可靠性以避免内存模板的损坏。该方法,将相应图分为paek和sidelobe,比如除了peak周围的窗口(用s表示)以外的其余像素。PSR可以表示为,其中和分别表示均值和sidelobe的标准差,表示peak值。在在线跟踪过程中,计算当前相应图的PSR的值为,以及之前的值的平均值为。本文只将满足条件的当前模板特征进入内存中,如果内存超出了限制,就将内存中最老的图像进行剔除。其计算过程如下所示
输入:视频序列和初始ground-truth
- 初始化内存M={},平均PSR ;
- 初始化模板特征以及更新后的模板特征
- for t = 2 to T do
- 提取当前搜索区域的特征X
- 通过计算和之间的互关系生成相应图
- 计算相应图的PSR值
- if then:
- 更新
- 添加当前的模板特征进入内存
- if 内存的大小 then
- 删除最老的模板特征
- 使用公式3,4计算内存中每个特征图中的通道重要性
- 使用公式5聚合历史表征得到
- 融合和对进行更新。
个人想法:这里有个疑问,为什么是选择最老的呢?因为老帧已经过去太久,时序关系不大了,所以舍弃吗?那是否可以将这个条件换成PSR值最小的内存模板特征舍去呢?仔细一想,因为PSR值小时相对于当时而言的,但时间变了,这个PSR值最小的意义是否还有呢?
Channel Decorrelation Regularization
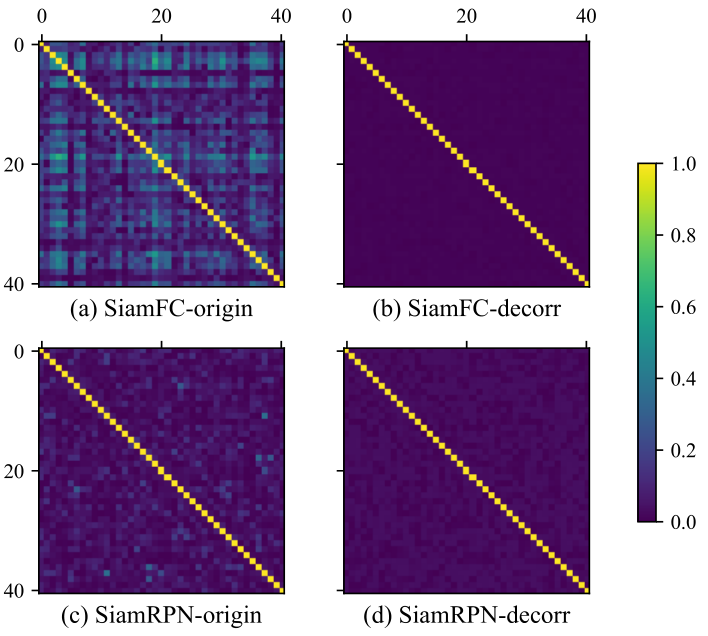
图3
为了清楚说明去相关损失的影响,本文给出了部分0~40的kernels在最后一层的相关矩阵绝对值。
a和c分别表示原始的SiamFC和SiamRPN,b和d分别表示去相关损失训练后的结果,其相关性显著下降。
Siamese的输出有明显的通道冗余(channel-wise redundancy)的不完全表示。如图3所示
为了获得通道间向光性较弱的优良特征嵌入(bedding),在最后一个卷积层引入去相关损失,负责生成用于跟踪的模板特征。值得注意的是,这种去相关正则化也将促进之前提到的时间相关性的模板更新机制。
在这个方法中,利用Pearson相关系数,去表示两个打平的卷积核和的相关性,他可以用如下公式进行计算
其中和是p和q的均值,和是p和q的标准差。假设最后一层存在K个卷积核,本文将这些卷积核重构为一维特征向量,并通过下面的公式计算去相关损失
其中C是Pearson相关系数矩阵,是单位矩阵,表示最后一层中第i和第j个卷积核之间的相关系数,和是C和I的第i行。
个人想法:原来是计算相关系数结合到损失函数中,通过梯度下降引导通道间相关性下降的嘛,妙啊。
在极大化函数下,着重与弱化大部分相关卷积核对的相关性。集合提出的去相关性正则化,最终的训练损失表示如下所示。
其中是原始Siamese跟踪器的训练损失函数,的值是基于一个启发式选择,他用来平和和。在SiamFC中,的计算方式与公式2相似。在SiamPRN中由两部分组成(分类损失和回归损失)。
training
整个框架可以方便地实现端到端的训练,更新模型仅包含两个全连接层和,分别对初始化模板和历史模板的通道上做线性变换,进行相似度的估计。和只有的参数。在线下训练时,首先随机选择一堆初始模板和搜索ptaches,然后从相同的视频中随机选择图像作为内存中的历史模板。如果视频的长度小于,就会使用多钟数据增强策略,比如水平翻转,高斯模糊,以及比例变换,来生成历史模板来模拟目标的变化。然后,提取原始模板和历史模板图像的特征,通过时间相关性融合这些特征,生成一个新的模板特征。最后,通过新模板和搜索特征之间的互相关生成匹配相应图。
Experiments
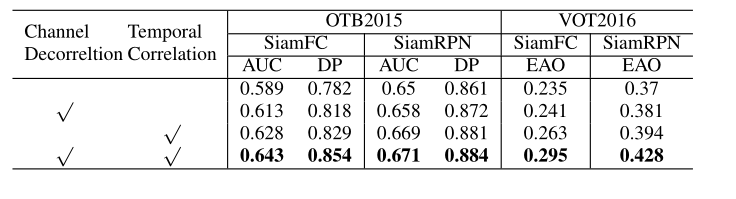
-
消融实验,单独使用通道去相关性和时间相关性进行训练,与baseline以及两者都使用进行对比。
-
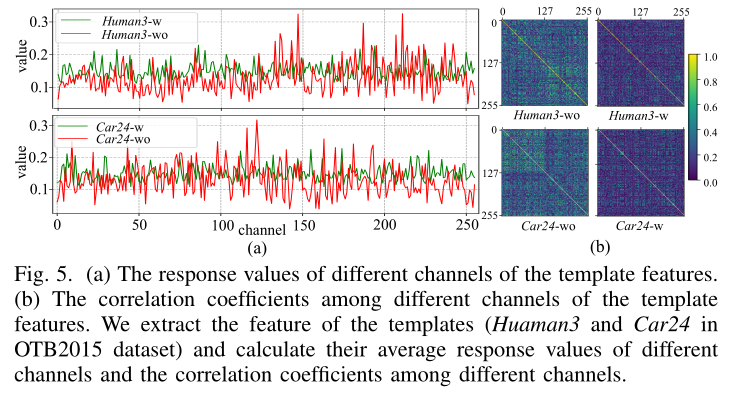
展示了模板特征不同通道的响应值以及模板特征不同通道之间的相关系数
-
在时间相关性的在线追踪过程中,使用了3种不同的策略保持内存中的数量
- 删除最老的
- 随机删除
- 删除PSR值最低的
个人想法:与之前的猜想对应上了,果然实验是检验真理的唯一标准,既然都有道理,试试就可以找到最好的了。
-
-
与SOTA的对比
-
在VOT2016的对比中,精度表现最好的是Siam Attn, 而添加了时间相关性和通道去相关性机制的SiamRPN得到了次之的成绩,但是其在速度上接近于SiamAttn的3倍
-
在VOT2018中的结果并没有比较出色的成绩,但是按照作者之前提过的这是要制作一个Siamese网络的Basline,如果Basiline直接超过了SOTA也不太合理,同时就算精度不如SiamAttn,但是已经超越了大部分的SOTA,且速度也比较可观。而且,自信看的话,和SOTA的差距也并没有很大

-
剩下就是在其他数据集上做差不多的实验,结果也都大同小异,也是通过大量不同数据集的验证证明这个方法的鲁棒性
-
-
与最近的更新策略进行对比
从结果上看,本文提出的时间相关性和通道去相关性提高了模板特征更新的能力,使得Siamese网络得到进一步发展。
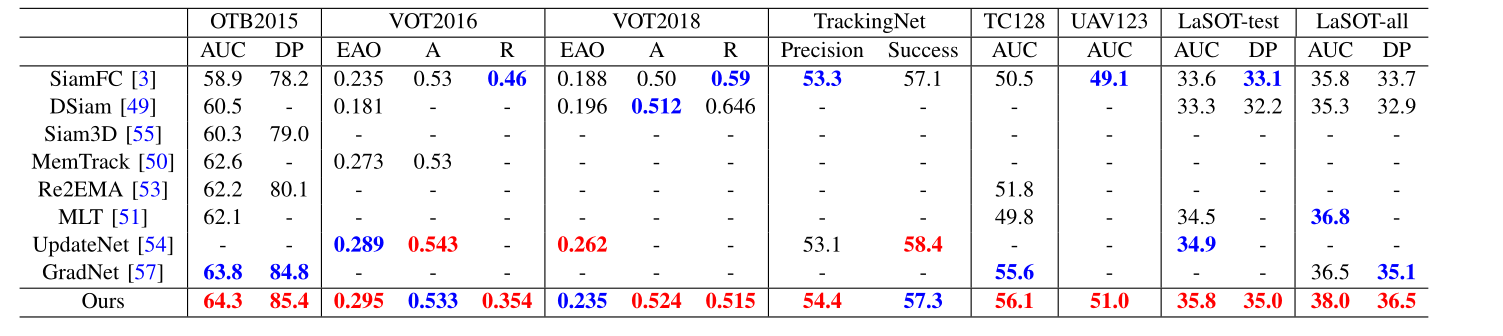
Experiments Analysis
结果分析:
在大部分的数据集上,相对于baseline都有明显的提升。
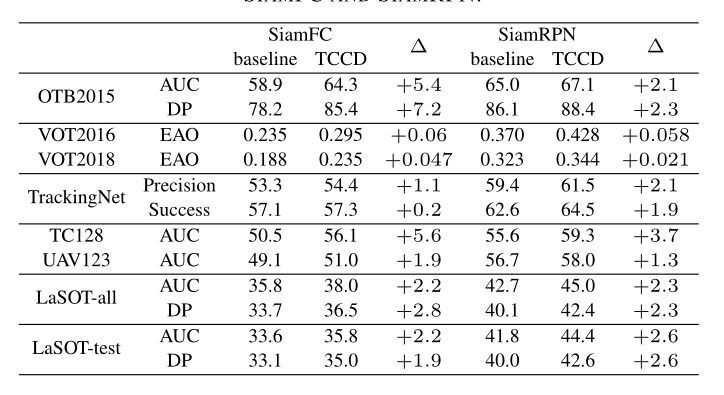
定性分析:这里主要是展示实际根据的视觉效果
失败案例:列举了一些跟踪失败的情况,并分析出由于目标与背景的相似度较高,所以会出现跟踪器漂移的情况。同时提出了作者的新目标,就是背景抑制。
个人想法:原来实验分析可以不用再实验描述部分一起写出来的么,原来分析还可以分成这三种种类的,我之前都以为只是对数据进行说明,简单说一下有些数值为什么好为什么不好。涨知识了




