Universal Weighting Metric Learning for Cross-Modal Retrieval

论文名称：Universal Weighting Metric Learning for Cross-Modal Retrieval

作者：Jiwei Wei; Yang Yang; Xing Xu; Xiaofeng Zhu;Heng Tao Shen

时间：2021-6

期刊：IEEE Transactions on Pattern Analysis and Machine Intelligence

Origin Abstract

Cross-modal retrieval has recently attracted growing attention, which aims to match instances captured from different modalities. The performance of cross-modal retrieval methods heavily relies on the capability of metric learning to mine and weight the informative pairs. While various metric learning methods have been developed for unimodal retrieval tasks, the cross-modal retrieval tasks, however, have not been explored to its fullest extent. In this paper, we develop a universal weighting metric learning framework for cross-modal retrieval, which can effectively sample informative pairs and assign proper weight values to them based on their similarity scores so that different pairs favor different penalty strength. Based on this framework, we introduce two types of polynomial loss for cross-modal retrieval, self-similarity polynomial loss and relative-similarity polynomial loss. The former provides a polynomial function to associate the weight values with self-similarity scores, and the latter defines a polynomial function to associate the weight values with relative-similarity scores. Both self and relative-similarity polynomial loss can be freely applied to off-the-shelf methods and further improve their retrieval performance. Extensive experiments on two image-text retrieval datasets, three video-text retrieval datasets and onefine-grained image retrieval dataset demonstrate that our proposed method can achieve a noticeable boost in retrieval performance.

Abstract

跨模态检索(Cross-modal)越来越被人关注，他的目标是匹配从不同模态捕获的实例。跨模态检索方法的性能在很大程度上依赖于度量学习的能力去挖掘和加权信息对。单模态检索任务已经的得到了充分的发展，但是跨模态检索任务的探索还不充分。在这篇文章中，作者提出了一个通用的加权度量学习框架来进行跨模态检索。这种方法可以有效地对信息对进行抽样，根据他们的相似度（similarity scores）设置合适的权重值，从而使不同的信息对具有不同的惩罚力度（penalty stength）。基于这个框架，作者引入了两种类型的多项式损失用于多模态检索，他们分别是自相似多项式损失（self-similarity polynomial loss）和相对相似多项式损失（relative-similarity polynomial loss）。前者提供了一个多项式函数去关联权重值和自相似度(self-similarity scores)，后者定义了一个多项式损失函数去关联权重值和相对相似度(relative-similarity scores)。这两个损失均可以用于线程的计算方法，并进一步提高检索性能。在两个图文检索数据集、三个视频文本检索数据集和一个细粒度图像检索数据集上进行的大量实验表明，该方法可以显著提高检索性能。

Introduction

跨模态检索是一项新兴的任务，他会从不同的模态中对实例进行检索。他已经被广泛研究过了，并且在现实中野有了多钟应用，比如：图文检索，视频文本检索，草图(Sketch-based)检索等。对比与单模态检索，由于不同模态之间固有的巨大差异，跨模态检索更具挑战性。跨模态检索的关键挑战在于测量出从不同模态中捕获的实例的相似度。

现有的跨模态检索方法侧重于学习一个共享的嵌入空间，使得不同模态的特征可以进行比较，从而弥补结构不同产生的鸿沟。总而言之，学习好的嵌入空间可以使得匹配的信息对聚集在一起，不匹配的信息对则会相差甚远，如图1所示。

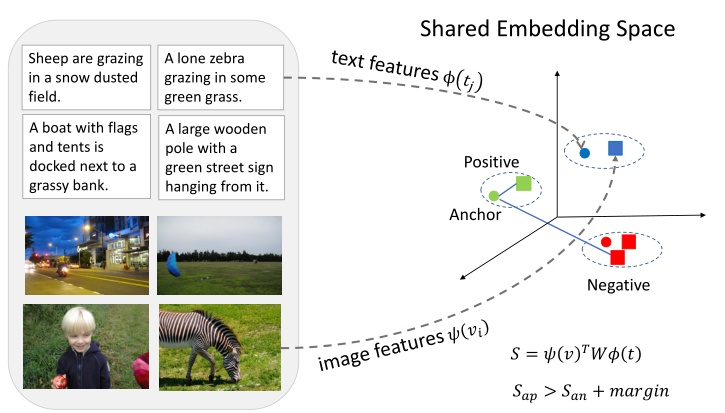
图1

现有的跨模态检索方法，试图将视觉特征 $\psi(v)$ 和文本特征 $\phi(t)$ 投射到一个共享的嵌入空间中。采用triplet损失对网络进行联合优化，使得正匹配对的相似度大于负匹配对。用图文检索作为一个例子，相同形状的点表示从同一个模态得到的。

近年来，人们提出了多种学习全局或局部区域对齐的方法，并采用不加权的triplet损失联合优化网络。有人提出了一种挖掘细粒度(fine-grained)区域字(region-word)对应的交互式匹配方案，并使用不加权的triplet损失去鼓励语义相关的实例聚集在一起。还有人提出了一种用于图文匹配的图结构匹配网络。

接下来开始引出问题（粗体字）

尽管这些方法取得了很大进步，但是他们中的大多数仍然使用不加权的triplet损失作为损失函数。然而，不加权的triplet损失平等对待不同的信息对，忽略了不同信息对之间的差异，导致了收敛速度慢，性能差。虽然已经提出了各种复杂的加权方案用于单模态检索，但由于模态间隔较大，适合于跨模态检索的方案很少。跨模态检索方法的性能非常依赖度量学习的能力去挖掘和加权信息对。因此对于跨模态检索来说引入合适的度量学习方法是重要的。

然后开始介绍自己的工作

为了解决上述的问题，本文引入了一种加权度量学习框架用于跨模态检索。最直观的动机就是给一个信息量更大的样本赋予更大的权重，这样不同的信息对就会有不同的惩罚力度。如图2所示。具体来说，正信息对的权重应该在它的相似度增加时减小，因为具有较大相似性得分的正信息对包含的信息较少。相对的，负信息对的权重应该在它的相似度增加时增加。相对相似度定义在正信息对和负信息对之间是不同的，即 $S_{ij}和S_{ii}$ 。相对相似度的权重应该在它的值增加时增加。

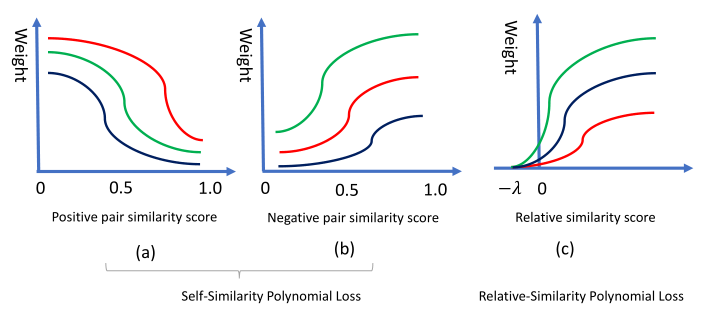
图2

正信息对的权值应该随着相似性得分的增加而减小，负信息对的权重应该随着相似性得分的增加而增大。对于相对相似度，他的权重值应该在相对相似度增加时增加。值得注意的是相对相似度的定义在正信息对和负信息对（即， $S_{ij}和S_{ii}$ ）之间之间是不同的。

在跨模态检索中，一个mini-batch中的每一个anchor，有许多的负样本，但是只有一个正样本。大多数负信息对的贡献较小，因为很少有负边界被破坏，用这些冗余信息对进行训练不会产生损失，这导致收敛缓慢并且模型性能差。在这篇文章中，选择最困难的样本作为信息对。对于所选择的信息对，本文定义了一个多项式函数，它根据信息对的相似度自适应地给他们赋予适当的权重。具体来说，作者在通用的加权度量学习框架下设计了两种多项式损失——自相似多项式损失和相对相似多项式损失。由于多项式函数可以拟合多种函数，他在克表示的损失函数方面提供了更大的灵活性。

本文的主要贡献如下：

在跨模态检索中引入了一种通用的加权度量学习框架，它可以有效地采样信息对并基于他们的相似度给他们设置合适的权重值，以便于不同的信息对得到不同的乘法力度
基于这个框架，设计了两种多项式损失。一种关联了权值与自相关度，另一种关联了权值与相对相似度。自相关度和相对相似度多项式损失都可以使用在现有的方法中吗，并且进一步增强其检索能力。
在两个基准数据集(MS-COCO和Flickr30K)上分别进行了图文检索和视频文本检索的三个基准数据集(MSVD,MSR-VTT和TGIF)上的大量实验。还评估了这个方法在细粒度的图像检索任务中的表现。实验结果表明，这个方法可以显著提升检索性能。

Realated Work

图文检索：

当前图文检索的主要方式是在图像和句子中构造一个共享的嵌入空间来减少不同类型数据的差异，以便于对图文对相似度进行计算。现有的检索工作包括两条研究线：全局对齐和局部区域对齐。全局对齐关注与学习整张图片和句子的一致性。而局部区域对齐学习的是局部图像区域和单词的一致性。

全局对齐：

PRF学习一个共同嵌入空间（co-embedding space）去实现图文检索
一种新的框架，将生成模型纳入到传统的特征嵌入中。
用一种基于图论推理网络生成全局可视化表征来实现图文检索
引入两个嵌入网络去分别获得图像和句子的表征
引入一种统一的VSE方法，该方法保留了邻域图像或句子之间的图结构来实现图文检索

局部对齐：

提出一种基于注意力的方法，利用注意力机制去获取图片和句子的一致性
SCAN学习局部区域和单词的潜在一致性
提出一种交互匹配模式去探索细粒度的区域字的一致性
引入一个多义(polysemous)实例嵌入网络去得到实例的多种表征
GSNN学习区域-字对齐

视频文本检索

当前视频文本检索的主流方法是构建视频和文本的共同嵌入空间来计算视频文本的相似度。在以前的文献中，视频和文本的全局表征被分开提取，他们的相似度就是用这两个全局表征进行计算的。

提出一种双重深度编码网络去生成密集的视频和句子的表征，并用不加权的triplet损失去优化网络。
提出一个协作专家(collaborative experts, CE）模型，通过聚合来自不同预训练模型的信息来生成视频片段的特征。
引入一个框架来利用多模态表征从而有效地实现视频文本匹配

尽管上面的方法非常有效，但是全局表征失去了细节信息。

另一种较少探索的方法是用局部对齐组件(比如每一帧和每一个词)来计算整个视频和文本的相似度。

引入一个多义实例嵌入网络去通过注意力机制去计算一个样本的表征。
通过一个分层的图结构对跨模态组件进行对齐。
提出Word2VisualVec，学习从文本输入预测视觉特征的表征。

度量学习

度量学习关注于学习一个距离度量函数来激励语义相关的实例彼此之间更加接近。

提出一种多相似度(multi-similarity)损失去实现信息对的采集和加权
提出一个hardness-aware深度度量框架，通过执行线性差值来自适应地操作样本的hardness-aware级别。
提出MDL-ALA的度量学习方法，它的目的是最大限度地提高学习度量的能力。
引入一个循环(circle)损失去加权不同的相似度

然而上述的方法是为单模态任务而开发的，这通常不能精准地捕获跨模组件与模态差距之间的关系。最近，针对跨模态的度量学习方法很少被实现。

尝试将图像和句子映射到同一个共同嵌入空间中，并使用不加权的triplet损失来激励语义相关实例聚集在一起
通过利用一个mini-batch中的难负样本提出了一个hard triplet损失。
DCML针对不同输入的特征学习非线性的转换。

然而上述的方法对待不同的信息对是平等的，这导致了模型收敛缓慢。在这篇文章中，作者提出了一种用于跨模态检索的新颖的度量学习方法。他可以有效采样信息对并基于他们的相似度赋予合适的权重，以便于不同的信息对得到不同的惩罚力度。

个人见解：上面加粗的句子已经出现了很多次了，作者在前面的章节中都至少提到过一次，紧扣文章主旨，同时用简短干练的语言，描述了不同的方法的工作方式以及不足，让没有接触过的读者很快对这个领域有了一个印象，到目前为止都写得很完美。

The Proposed Approach

Probelm Statement

让 $V=\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \cdots, \mathbf{v}_{n}\right\}$ 和 $T=\left\{\mathbf{t}_{1}, \mathbf{t}_{2}, \cdots, \mathbf{t}_{n}\right\}$ 表示从两个不同的模态中获取的实例集合。 $\mathbf{v}_{i} \in \mathbb{R}^{d_{1}}$ 是视觉特征向量， $\mathbf{t}_{i} \in \mathbb{R}^{d_{2}}$ 是文本特征向量，其中 $d_1$ 和 $d_2$ 是特征维度。令 $\left(\mathbf{v}_{i}, \mathbf{t}_{j, i \neq j}\right)$ 表示一个负信息对， $\left(\mathbf{v}_{i}, \mathbf{t}_{i}\right)$ 表示一个正信息对。对于每一个查询，跨模态检索的目标是从另一个模态中检索出与他相关的实例。跨模态检索的核心思想是计算从不同模态中捕获的特征的相似度。在之前的参考文献中，为了减少heterogeneous gap，人民提出了许多方法来构建一个共同的嵌入空间。在这个共同的嵌入空间中，一个project函数 $S(\mathbf{v}, \mathbf{t} ; \mathbf{W})=\psi(\mathbf{v})^{T} \mathbf{W} \phi(\mathbf{t})$ 被定义去计算视觉表征 $\psi(\mathbf{v})$ 和句子表征 $\phi(\mathbf{t})$ 之间的相似度。 $\mathbf{W}$ 是要学习的映射矩阵。我们希望负信息对的相似度大大小于正信息对的相似度，于是就有了公式1,2的约束

$\begin{aligned} 公式1：&S\left(\mathbf{v}_{i}, \mathbf{t}_{i}\right)>S\left(\mathbf{v}_{i}, \mathbf{t}_{j, j \neq i}\right)+\lambda_{0}, \forall \mathbf{v}_{i} \\ 公式2：&S\left(\mathbf{v}_{j}, \mathbf{t}_{j}\right)>S\left(\mathbf{v}_{i, i \neq j}, \mathbf{t}_{j}\right)+\lambda_{0}, \forall \mathbf{t}_{j} \end{aligned}$

其中 $\lambda_0$ 是一个边界(margin)

对于双向检索任务（bidirectional retrieval tasks）传统的不加权的triplet损失定义如过时3所示

$公式3：L=\left[S(\mathbf{v}, \hat{\mathbf{t}})-S(\mathbf{v}, \mathbf{t})+\lambda_{0}\right]_{+}+\left[S(\hat{\mathbf{v}}, \mathbf{t})-S(\mathbf{v}, \mathbf{t})+\lambda_{0}\right]_{+},$

其中，对于每一个每一个anchor $\mathbf{v}$ 来说， $(\mathbf{v},\hat{\mathbf{t}})$ 是的一个mini-batch中的一个负信息对。 $[t]_{+}=max(0,t)$ 。值得注意的是，对于交叉检索任务，在一个小批量中，每个anchor有许多负样本但只有一个正样本。triplet损失是跨模态检索的主要目标函数。然而triplet损失对待不同的不同的信息对是相等的，导致模型收敛慢，效果差。本文提出了一个通用的加权度量学习方法去选择信息对并根据他们的相似度赋上合适的权重。（再次点题）

$N_{\mathbf{v}_{i}}=\left\{S_{i j, i \neq j}\right\}$ 和 $N_{\mathbf{t}_{j}}=\left\{S_{i j, j \neq i}\right\}$ 分别表示实例 $\mathbf{v_i}$ 和 $\mathbf{t_j}$ 的所有负信息对的相似度集合。 $S_{i,j}$ 是一个实数，其表示视觉特征 $\mathbf{v_i}$ 和文本特征 $\mathbf{t_j}$ 的相似度。度量学习的关键是使得正信息对更加聚合，负信息对彼此分离。现有的加权方法给出了一个特殊的函数来表示权值与相似度之间的关系，该函数的形式因任务而异。本文引入了一种通用的加权度量学习框架去统一这些损失函数

$公式4：\begin{aligned} L &=\frac{1}{K} \sum_{i} \sum_{N_{\mathbf{v}_{i}}}\left[G_{P o s} S_{i i}+G_{N e g} S_{i j, i \neq j}+\lambda_{0}\right]_{+} \\ &+\frac{1}{K} \sum_{j} \sum_{N_{\mathbf{t}_j}}\left[G_{P o s} S_{j j}+G_{N e g} S_{i j, i \neq j}+\lambda_{0}\right]_{+} \end{aligned}$

其中K表示一个mini-batch中信息元组的数量。 $G_{Pos}$ 和 $G_{Neg}$ 是权值，他们的定义如公式5,6

$\begin{aligned} 公式5：G_{P o s} &=G\left(S_{i i}, N_{\mathbf{v}_{i}}\right) \\ 公式6：G_{N e g} &=G\left(S_{j j}, N_{\mathbf{t}_{j}}\right) \end{aligned}$

其中 $G(\cdot)$ 是联系权值和相似度分数的函数。值得注意的是 $G(\cdot)$ 是有正负之分的(signed)。以广泛使用的triplet损失作为例子， $G_{Pos}=-1, G_{Neg} = 1$ 。理论上， $G_{Pos}$ 和 $G_{Neg}$ 的形式是不同的，他们都可以被定义为一个相对相似度或自相似度的函数，如图3所示。如果 $G(\cdot)$ 是一个自相似度的函数(a function of self-similarity scores)，正信息对的权值应该随着其相似度的增加而减小，而负信息对的权值应该随着相似度的增加而增加。具有较大相似度的正信息对和具有较小相似度的负样本对包含的信息较少（模型已经很好地适用于这些信息对了）。如果 $G(\cdot)$ 是一个相对相似度的函数(a function of relative-similarity scores)，权值应该随着相对相似度的增加而增加，如图2的c所示。公式4是一个通用公式，只要稍加修改就能退化成triplet损失。

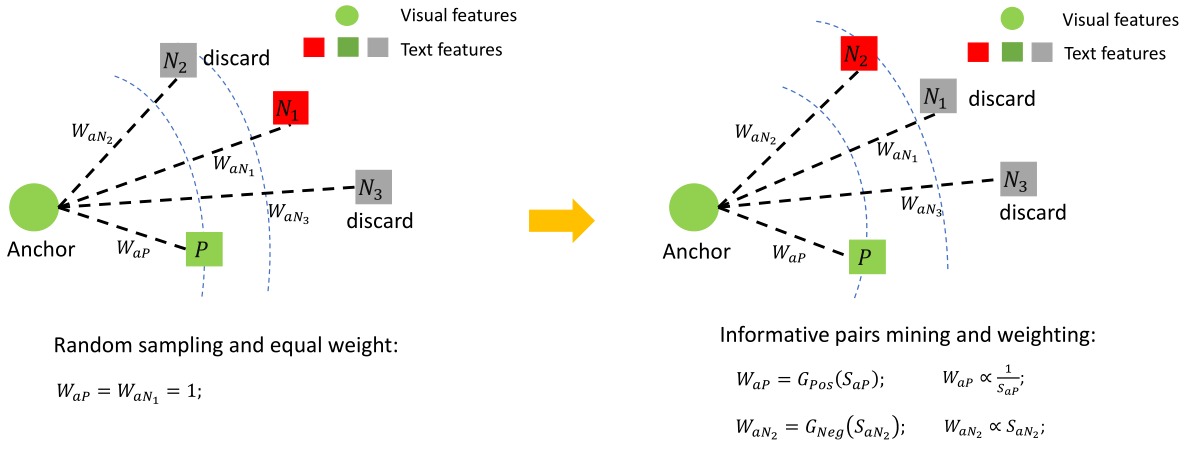
图3 跨模态检索通用加权度量学习框架图

相同形状的点表示来自相同的模态。P是一个anchor(anchor表示的视觉特征向量)中唯一的正样本。 $N_1，N_2，N_3$ 是一个anchor的负样本。左标是样本采样策略(Simple sampling strategy)，右边是通用加权度量学习框架（Universal weighting metric learning framework）

对于跨模态检索来说，在一个mini-batch的每一个anchor中，有许多的负样本但是只有一个正样本。对于大多数负信息对来说信息量较小，用这些冗余信息对进行训练不会有损失值。在文章中，作者选择了一个mini-batch中最难的样本作为信息对，即 $Max\{N_{\mathbf{v}_i}\}$ 和 $Max\{N_{\mathbf{t}_j}\}$ 。理论上， $G(\cdot)$ 是联系权值和相似度的函数。

Self-similarity polynomial loss

自相似多项式损失定义了一个联系权值和自相似度的多项式函数。具体来说，令 $G(\cdot)$ 作为相似度的多项式函数，对于正信息对 $(\mathbf{v}_i,\mathbf{t}_i)$ ，他的权重函数 $G_{Pos}$ 可以被定义为公式7

$公式7：G_{P o s}=a_{p} S_{i i}^{p}+a_{p-1} S_{i i}^{p-1}+\cdots+a_{1} S_{i i}+a_{0}$

其中 $\left\{a_{i}\right\}_{i=0}^{i=p}$ 是超参数， $p$ 是一个正数，代表多项式函数的顺序。因为多项式函数可以拟合多钟函数，所以 $G_{Pos}$ 是灵活的。正信息对的权值应该在他的相似度增高时减小。对于选择的负信息对 $(\mathbf{v}_i,\mathbf{t}_j)$ ，他的权重函数 $G_{Neg}$ 可以被定义为公式8

$公式8：G_{N e g}=b_{q} S_{i j}^{q}+b_{q-1} S_{i j}^{q-1}+\cdots+b_{1} S_{i j}+b_{0}, i \neq j$

其中 $\left\{b_{i}\right\}_{i=0}^{i=q}$ 是超参数，q是一个正数。于正信息对相比，负信息对的权值应该在相似度增加的时候增加。

个人疑问：公式7和8的a和b是超参数(hyper-parameters)么，是的话要手动设置这么多个参数，不会比较麻烦么。有没有一种可能就是这里的参数用可学习的参数进行替换会更合适一些。先看看实验有没有这部分的说法吧。

不同信息对的权重可以通过公式7,8获得。自相关多项式损失 $L_{Self}$ 可以用公式9表示

$\begin{aligned} 公式9：L_{S e l f} &=\frac{1}{N} \sum_{i=1}^{i=N}\left[G_{P o s} S_{i i}+G_{N e g} \max _{S_{i j} \in N_{\mathbf{v}_{i}}}\left\{S_{i j}\right\}+\lambda_{1}\right]_{+} \\ +& \frac{1}{N} \sum_{j=1}^{j=N}\left[G_{P o s} S_{j j}+G_{N e g} \max _{S_{i j} \in N_{\mathbf{t}_{j}}}\left\{S_{i j}\right\}+\lambda_{2}\right]_{+} \cdot \end{aligned}$

将公式7,8带入公式9，可以得到

$\begin{aligned} 公式10：L_{S e l f}=& \frac{1}{N} \sum_{i=1}^{i=N}\left[\sum^{P} a_{p} S_{i i}^{p}+\sum^{Q} b_{q} \max _{S_{i j} \in N_{\mathbf{v}_{i}}}\left\{S_{i j}\right\}^{q}\right]_{+}+\\ & \frac{1}{N} \sum_{j=1}^{j=N}\left[\sum^{P} a_{p} S_{j j}^{p}+\sum^{Q} b_{q} \max _{S_{i j} \in N_{\mathbf{t}_{j}}}\left\{S_{i j}\right\}^{q}\right]_{+}, \end{aligned}$

其中 $P,Q$ 是正数，分别表示 $G_{Pos}$ 和 $G_{Neg}$ 的最高阶。p和q的最小值是0

对于选定的信息对，自相关损失可以自适应地不同的信息对赋予适当的权重，因为多项式损失可以拟合多种函数，他在可表示的损失函数方面提供了更大的灵活性。可以通过限制多项式函数的阶数来降低超参数。

Relative-similarity polynomial loss

在公式4中， $G(\cdot)$ 是一个联系权重和相似度的函数，一个复杂的 $G(\cdot)$ 能够使得模型取得更好的性能。然而，实际上，更多的超参数增加了 $G(\cdot)$ 的复杂性。在这个小节，作者将介绍一个先进的基于作者提出的通用加权度量学习框架的相对相似多项式损失。作者通过限制 $G(\cdot)$ 的阶数减少了超参数。相对相似多项式损失为相对相似度赋予适当的权重，具体来说，令 $G(\cdot)$ 是一个相对相似度的函数，对于每个选择的triplet $\{\mathbf{v}_i,\mathbf{t}_i,\mathbf{t}_j\}$ ，它的权重函数 $G_{rel}$ 可以被定义为公式11

$公式11：G_{r e l}=e_{0}+e_{1}\left(S_{i j}-S_{i i}\right)+\cdots+e_{p}\left(S_{i j}-S_{i i}\right)^{p}$

其中 $\{e_p\}$ 是超参数， $p$ 是一个正数，相对相关多项式损失函数，可以用公式12和公式13表示

$\begin{array}{r} 公式12：L_{R e l}=\frac{1}{N} \sum_{i=1}^{i=N}\left[G_{r e l} * \max _{S_{i j} \in N_{v_{i}}}\left(S_{i j}-S_{i i}\right)+\lambda_{1}\right]_{+}+ \\ \frac{1}{N} \sum_{j=1}^{j=N}\left[G_{r e l} * \max _{S_{i j} \in N_{t_{j}}}\left(S_{i j}-S_{j j}\right)+\lambda_{2}\right]_{+} ，\\ G_{r e l}=G\left(S_{i j}-S_{i i}\right) \end{array}$

通过公式12，可以转化为：

$\begin{aligned} 公式13：L_{R e l}=& \frac{1}{N} \sum_{i=1}^{i=N}\left[\sum_{p=0}^{p=P} e_{p} * \max _{S_{i j} \in N_{\mathbf{v}_{i}}}\left(S_{i j}-S_{i i}\right)^{p}\right]_{+}+\\ & \frac{1}{N} \sum_{j=1}^{j=N}\left[\sum_{p=0}^{p=P} e_{p} * \max _{S_{i j} \in N_{\mathbf{t}_{j}}}\left(S_{i j}-S_{j j}\right)^{p}\right]_{+} . \end{aligned}$

自相似和相对相似多项式损失函数都统一在公式4中定义的通用加权框架中。与自相关多项式损失相比，相对相似多项式损失几乎没有超参数，且易于收敛。值得注意的自相似和相对相似多项式损失可以通过随机梯度下降优化。

Gradient Analysis

本文导出了自相似多项式损失关于 $S_{ii}$ 和 $S_{ij}$ 的梯度(忽略了公式10中的常数项 $\frac 1N$ )

$\begin{aligned} &公式14：\frac{\partial L_{S e l f}}{\partial S_{i i}}=\sum_{p=1}^{p=P} p a_{p} S_{i i}^{p-1}\\ &公式15：\frac{\partial L_{S e l f}}{\partial S_{i j}}=\sum_{q=1}^{q=Q} q b_{q} S_{i j}^{q-1} \end{aligned}$

其中 $\frac{\partial L_{S e l f}}{\partial S_{i i}} \leq 0$ ， $\frac{\partial L_{S e l f}}{\partial S_{i j}}\geq 0$

本文还导出了相对相似多项式损失关于 $S_{ii}$ 和 $S_{ij}$ 的梯度(忽略了公式13中的常数项 $\frac 1N$ )

$\begin{aligned} 公式16：\frac{\partial L_{R e l}}{\partial S_{i i}} &=-\sum_{p=1}^{p=P} p e_{p}\left(S_{i j}-S_{i i}\right)^{p-1} \\ 公式17：\frac{\partial L_{R e l}}{\partial S_{i j}} &=\sum_{p=1}^{p=P} p e_{p}\left(S_{i j}-S_{i i}\right)^{p-1} \end{aligned}$

其中 $\frac{\partial L_{Rel}}{\partial S_{i i}} \leq 0$ ， $\frac{\partial L_{Rel}}{\partial S_{i j}}\geq 0$

如公式14,15中所示， $L_{self}$ 允许每个相似度以自己的速度学习。triplet损失为不同的相似度提供了一个恒定的梯度范围 $\left(\frac{\partial L_{\text {triplet }}}{\partial S_{i i}}=-1, \quad \frac{\partial L_{\text {triplet }}}{\partial S_{i j}}=1\right)$ ，这损害了模型的灵活性。相对的，自相似多项式损失通过考虑每个相似度的hardness来确定梯度的大小。如公式16,17所示，相对相似多项式损失通过考虑相对相似度来确定梯度的大小，进一步增强了优化的灵活性。简单的正负信息对的梯度尺度较小，而难的正负样本对的梯度尺度较大，这个特性使得 $L_{Self}$ 和 $L_{Rel}$ 能够为模型提供丰富的监督信号

个人见解：看到这里，我是真的佩服这篇文章，这么多数学公式可见作者的数学功底非常深厚。并且与传统的那种计算机视觉论文不同，这里更加关注的是设计的合理性，这个合理性是通过数学分析而得出来了，将深度网络可解释性的想法体现出来了。这种文章是最值得一看的，一个是学习到了针对任务的损失设计，另一个就是使得这个方案更加合理，更加可靠。

Experiments

Hyper-parameters Selection

多项式损失中的超参数如 $\{a_p\}$ 和 $\{b_q\}$ 是在验证集上通过网格搜索(grid search)选择的。

个人疑问：这里多项式函数设置了默认的多项式阶数为2，也就意味着，这相于默认是一个二次函数。之前在数学建模备赛时好像有学习到，未知拟合的情况下1阶2阶的函数其实都不太合理，因为他们要么拟合简单的曲线，要么拟合直线，这对复杂的数据集作用比较微弱。所以我觉得这个多项式阶数，应该最小也要从3阶往上。还有就是超参数范围的选择上是否有说法，还是经验得到的，虽然我认可文中所说a0和b0的作用不大，但是确实这个超参的选择范围让我有点迷惑。

datasets and method

Image-Text Retrieval Datasets
1. MS-COCO
2. Flickr30K
Image-Text Retrieval Method
1. SCAN(Stacked Cross Attention Network)
  1. 目的是通过堆叠的cross attention学习区域-字的对应
  2. MS-COCO使用自相似多项式函数，Flickr30K使用相对相似多项式损失函数，使用grid search的方式设置多项式损失的超参数
2. GSMN(Graph Structured Matching Network)
  1. 目的是通过图结构匹配网络来学习细粒度短语(phrase)的图文匹配对应
  2. 使用相对相似多项式损失函数
Video-Text Retrieval Datasets
1. MSVD
2. MSR-VTT
3. TGIF
Video-Text Retrieval Method
1. Collaborative Experts(CE)
  1. 是一个通过聚合来自不同预训练模型的信息，为每个视频片段生成密集的表征框架
  2. 使用了自相对多项式损失和相对相似多项式损失。
2. Hierarchical Graph Reasoning(HGR)
  1. 通过分层图结构网络对跨模态组件进行对齐
  2. 使用了相对相似多项式损失

Result

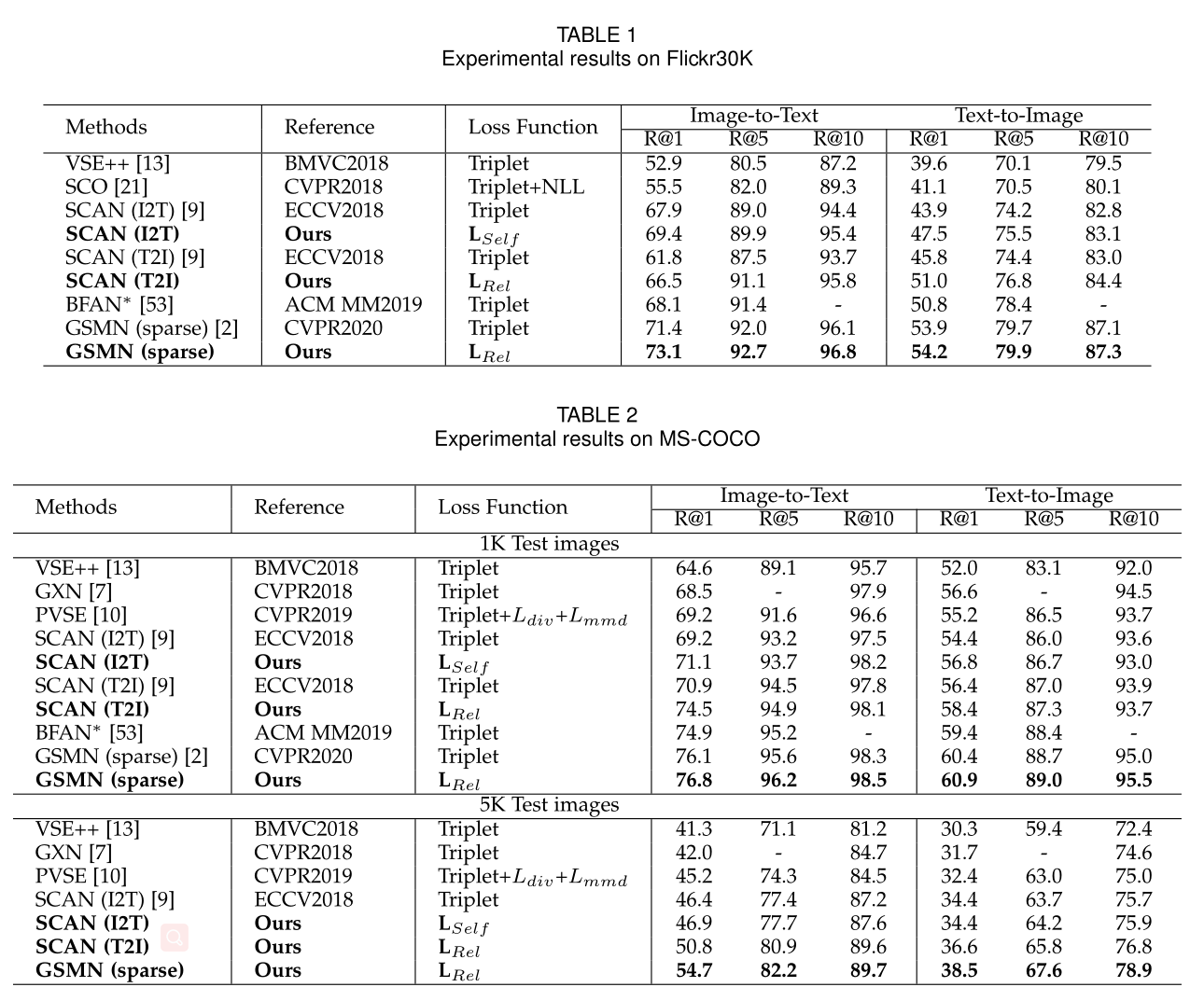
Image-Text Retrieval

总结一下：相对相关多项式损失的结果通常比自相关多项式损失好一些，应为相对相关多项式损失联系权重和相对相似度，其有更少的超参数，更容易收敛。

Video-Text Retrieval Results

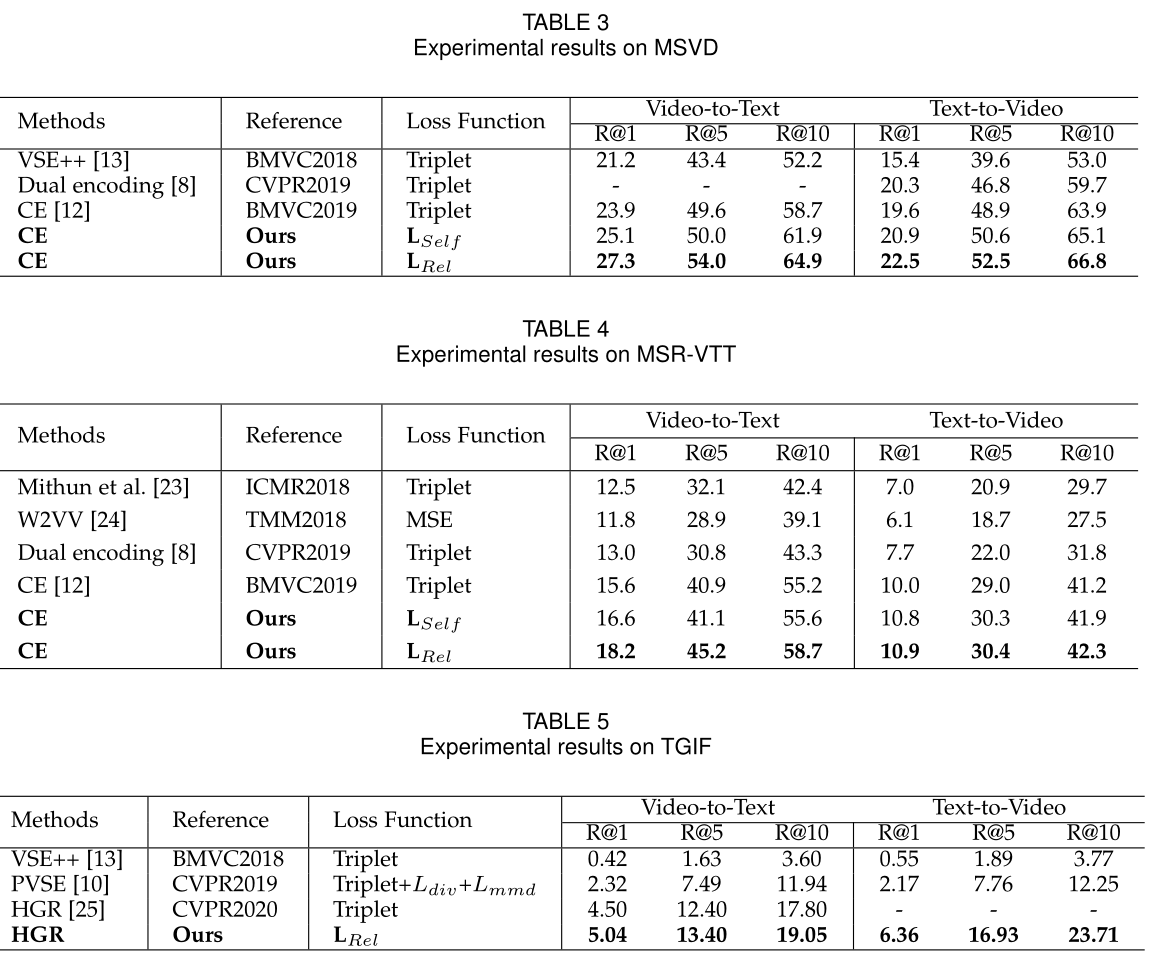
Ablation Study

由于负样本的权重对模型性能影响较大，所以只考虑负样本的函数 $G_{Neg}$ 的超参数 $\{b_q\}$ ，在MSR-VTT上的实验结果如下(图中的数值是自相似度多项式函数在CE上使用计算出的Recall@1，在负信息对上)
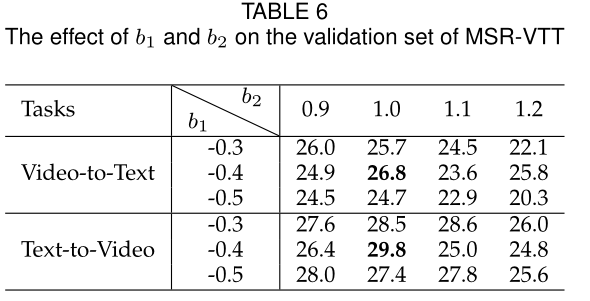
使用相对相似多项式损失在GSMN上，在Flickr30K上的Recall@1结果如下图

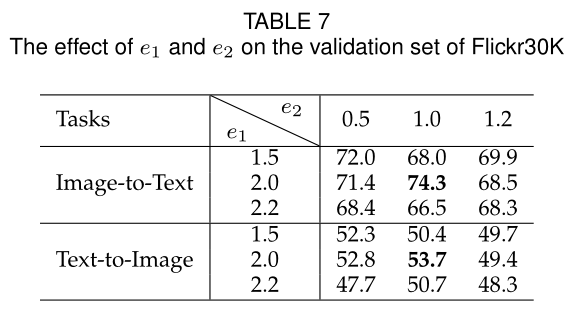
triplet损失和相对相似多项式损失
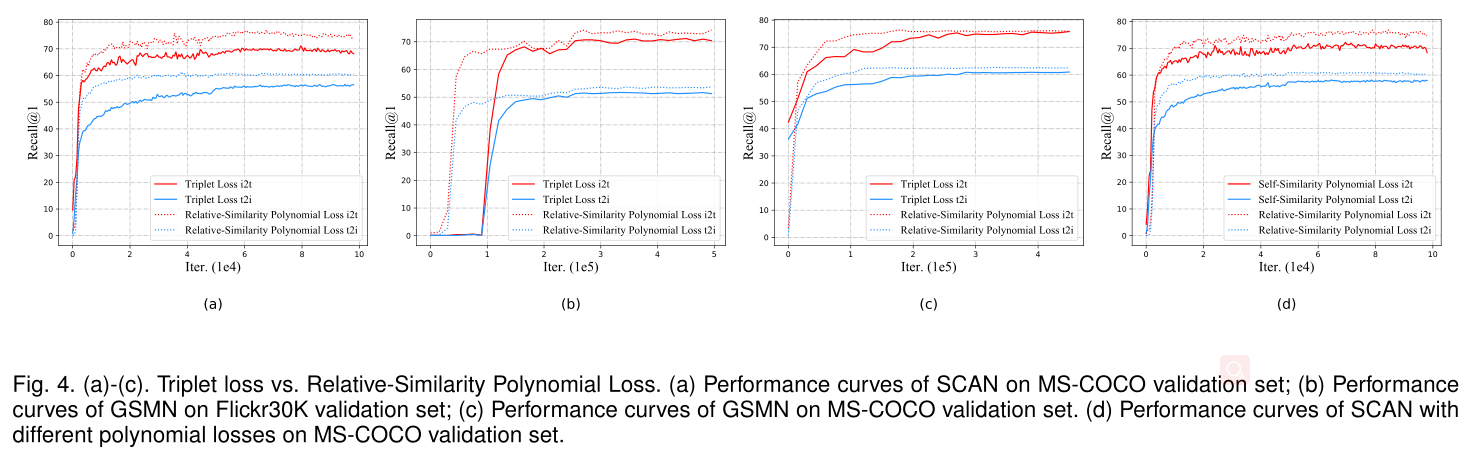
自相关和相对相关多项式损失

如图四，主要是比较不同方法的性能，从曲线也可以看出模型的收敛速度
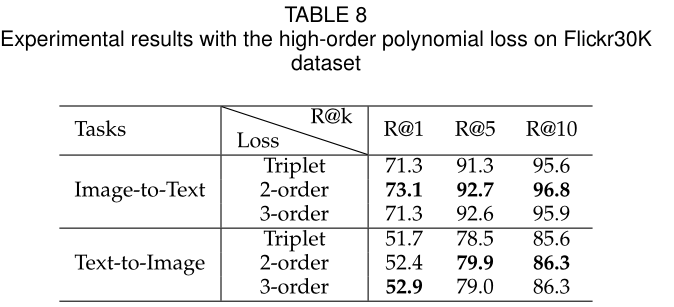
高阶的多项式损失

使用3阶的相对相似多项式损失在GSMN上进行实验，结果如下表所示，实验结果3阶应该会比2阶好，但是出现了相反的情况，应该是参数没有设置好，但是仅仅只用二阶就可以得到出色表现了。今后会尝试使用NAS和meta-learning的技术选择超参数。

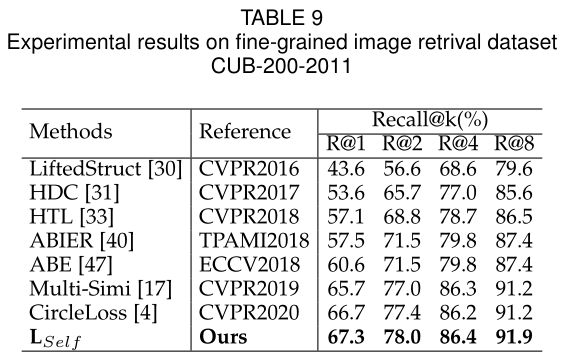
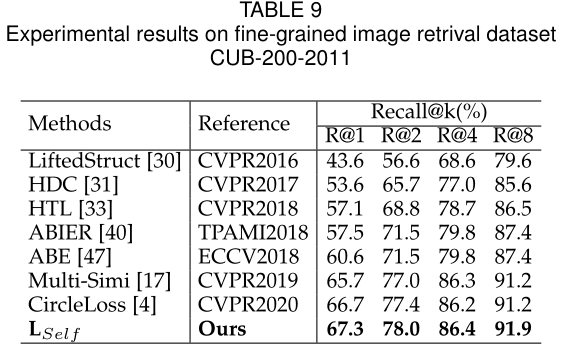
Fine-Grained Image Retrieval

Qualitative Results

学习总结：

本文提出了一种通用的度量学习方法用在跨模态检索上，分别是自相似多项式损失和相对相似多项式损失，前者希望正信息对的相似度增加时，损失减小，负信息对相似度增加时损失增加，而后者希望当相似度增加时，损失也跟着增加。连着都是为了利用难样本中的额外信息，对不同模态的内容进行检索。思路很新颖，但是仍然有一个疑惑，就是他的超参数设置问题，这个超参数的定界让我摸不着头脑，这个定界是经验值还是直观选的，如果把超参数换成可以通过梯度下降学习的可变参数，度量学习的效果会不会更好一些。希望能够有人解答。