「数据结构」数据结构复习

树

树是n个结点的有限集，它或为空树(n=0)，或为非空树，对于非空树 $T$ :

有且仅有一个称为根的结点
除根结点外，其余结点可分为m(m>0)个互不相干的有限集合 $T_1,T_2,...,T_m$ ，其中每一个集合本身又是一棵树，并且称为根的子树。

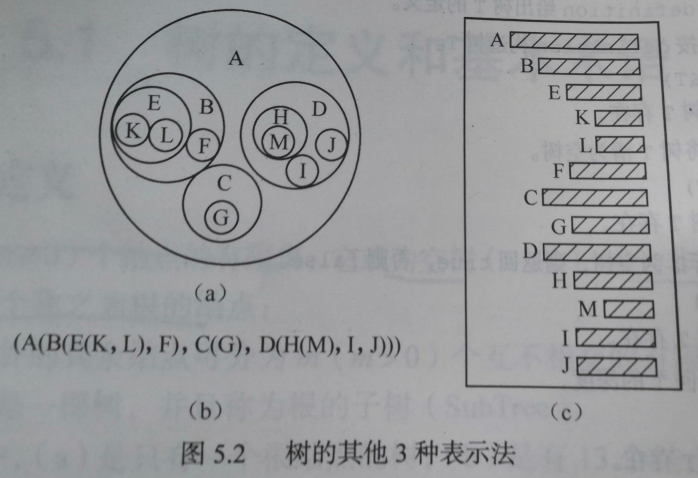
a集合形式的树：对于任意两个集合，他们要么不想交，要么其中一个包含另一个

b广义表表示的树：根作为子树森林组成的表的名字写在表的左边。

c凹入法表示的数（类似书的编目）

二叉树

二叉树是n个结点所构成的集合，它或为空树(n==0)，或为非空树，对于非空树 $T$

有且仅有一个称为根的结点
除根结点以外的其余结点分为两个互不相交的子集 $T_1$ 和 $T_2$ ，分别称为T的左子树和右子树，且都是二叉树

二叉树和树的区别

二叉树每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点）

二叉树的子树有左右之分，其次次序不能任意颠倒

二叉树的性质（重点）

（ps：默认二叉树的根结点在第1层）

性质1：在二叉树的第i层上至多有 $2^{i-1}$ 个结点( $i\geq1$ )

性质2：深度为k的二叉树至多有 $2^k-1$ 个结点

每层有 $2^{i-1}$ 个，然后有k层，就是 $2^0+2^1+2^2+....+2^{k-1}$ ，即以2为公比的等比数列，根据等比数列公式 $\frac{2^0\times(1-2^{k-1})}{1-2}=\frac{1-2^{k-1}}{-1} = 2^{k-1}-1$

性质3：对任何一棵二叉树T，如果其叶子结点数为 $n_0$ ，度为2的结点数为 $n_2$ ，则 $n_0=n_2+1$

设 $n_1$ 为二叉树T中度为1的结点数，因为二叉树中所有结点的度均小于等于2

所以： $n = n_0+n_1+n_2$

二叉树是一个无环的图，所以他的结点数和边数B，满足 $n = B+1$ ，由于这些边是由度为1或2的结点出发，所以有 $n = n_1+2n_2+1$ ，带入到上式可得

$n_0+n_1+n_2 = n_1+2n_2+1$ 即 $n_0 = n_2+1$

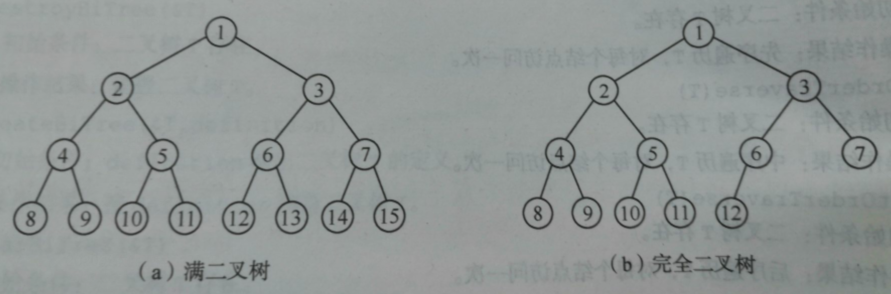
满二叉树：深度为k且含有 $2^k-1$ 个结点的二叉树，其在每一层上的结点数都是最大结点数

对树从上到下，从左到右进行编号，若一棵深度为k的二叉树，有n个结点，并且其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，则这棵二叉树是完全二叉树

完全二叉树的特点

叶子结点只可能在层次最大的两层上出现
对任意结点，若其右分支下的子孙的最大层次为l，则其左分支下的子孙的最大层次必为l或l+1

性质4：具有n个结点的完全二叉树的深度为 $\lfloor log_2n+1 \rfloor$

$2^{k-1}-1<n\leq2^k-1$ 或 $2^{k-1}\leq n<2^k$

所以有 $k-1\leq logn < k$ ，因为k是整数，所以logn要下取整

性质5：如果对一棵有n个结点的完全二叉树的结点按照层序编号，则对任一结点i $(1 \leq i\leq n)$ 有

如果i=1，则结点i是二叉树的根，无双亲，如果i>1，则双亲结点是 $\lfloor \frac i2 \rfloor$
如果 $2i > n$ ，则结点i无左孩子(结点i为叶子结点)，否则左孩子是结点2i
如果 $2i+1>n$ ，则结点无右孩子，否则右孩子是 $2i+1$

二叉树的存储结构

顺序存储结构，按照完全二叉树编号的方式存储，其编号为对应的索引，为了操作简单，在代码中的实现，将结点x的左孩子坐标用x<<1表示，而其右孩子可用x<<1|1进行表示
链式存储结构：使用结构体的方式进行存储，包括左右结点指针和当前的值，必要情况下，还可以添加双亲结点的编号

二叉树的遍历

先序遍历—— $根结点\rightarrow左子树\rightarrow右子树$
中序遍历—— $左子树\rightarrow根结点\rightarrow右子树$
后序遍历—— $右子树\rightarrow左子树\rightarrow根结点$
层序遍历——利用队列存储每一层的结点，然后将结点出队的同时，将其左右子树加入，当队列为空是遍历结束。

根据结点的遍历顺序还原二叉树(重点)

至少两种遍历方式，且一定要带有中序遍历，不然的话没有救

性质：

前序遍历的第一结点一定是根结点
中序遍历根据根结点分成左右子树
后序遍历的最后一个结点一定是根结点

来个例题

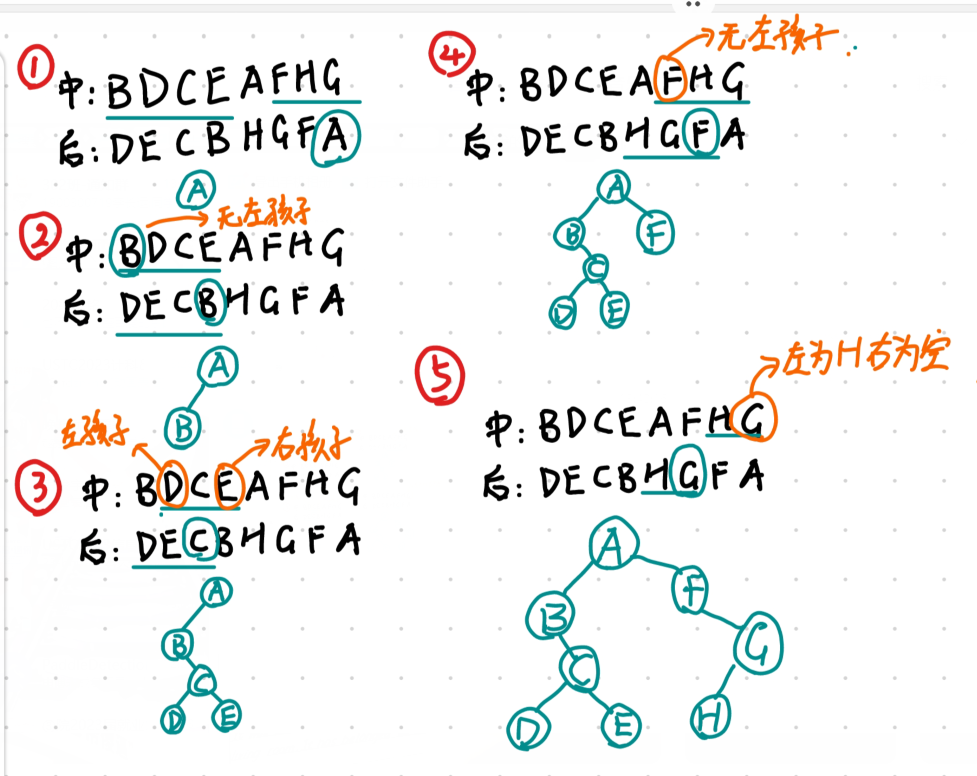
中序遍历：BDCEAFHG

后序遍历：DECBHGFA

A一定是根结点，左右子树集合分别是{BDCE}，{FHG}

然后根据{BDCE}对应到后续遍历中(前面4个元素)，第四个元素是B说明左子树的第一个结点是B，再看回中序，发现B的左边没有了，说明B没有左孩子。(其他同理就行了）

最终结果：‘’

森林与二叉树的转换

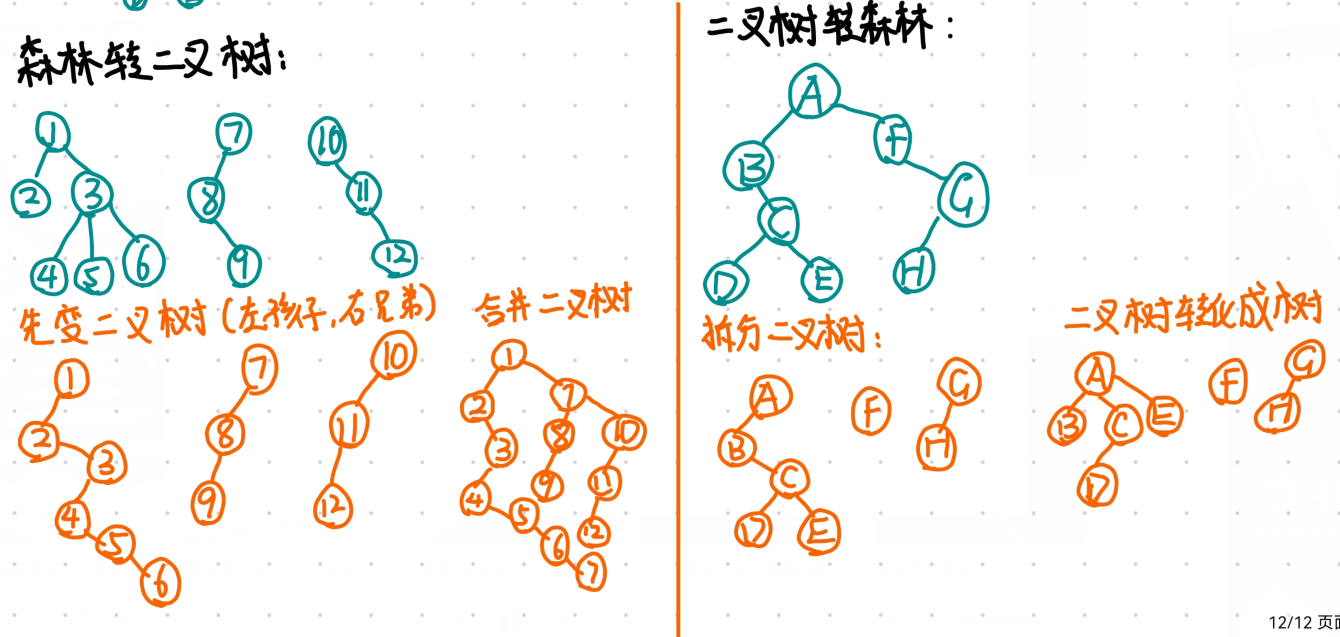
首先要介绍一下怎么把一棵树转化成一个二叉树的形式，这个比较简单，就是将新转化的二叉树结点的左边表示这个结点的孩子，右边表示这个结点的兄弟即可。

森林转化成二叉树：就是先将森林中每一颗树的形式转化成二叉树，然后选择一棵二叉树的根，将其余二叉树的根插入到这个结点的右子树即可。

二叉树转换成森林：首先将二叉树的右结点递归地拆除，然后按照二叉树结构的树的定义还原森林中的每一颗树就可以了。

证明：一棵二叉树的先序序列和中序序列可惟一确定这棵二叉树。

设一棵二叉树的先序序列和中序序列分别存放在一维数组A[1..n]和B[1..n]中。

因为先序序列的第一个节点A[1]为二叉树的根节点，在中序序列中找到与A[1]相同的节点，不妨令B[i]=A[1]

因为二叉树的任何一棵子树的节点是紧挨在一起的

所以构造的二叉树的左子树由先序序列A[2..i]和中序序列B[1..i-1]确定的二叉树构成，而所构成的二叉树的右子树由先序序列A[i+1..n]和中序序列B[i+1..n]确定的二叉树组成。

这是一个递归过程，当先序序列和中序序列分别有3个一下的节点时，可唯一确定对应的二叉树。

因此，由一棵二叉树的先序序列和中序序列可以唯一确定这棵树

图

简单路径、简单环、简单路径：序列中顶点不重复出现的路径称为简单路径，除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路，称为简单回路和简单环，欧拉回路

AOE网的关键路径

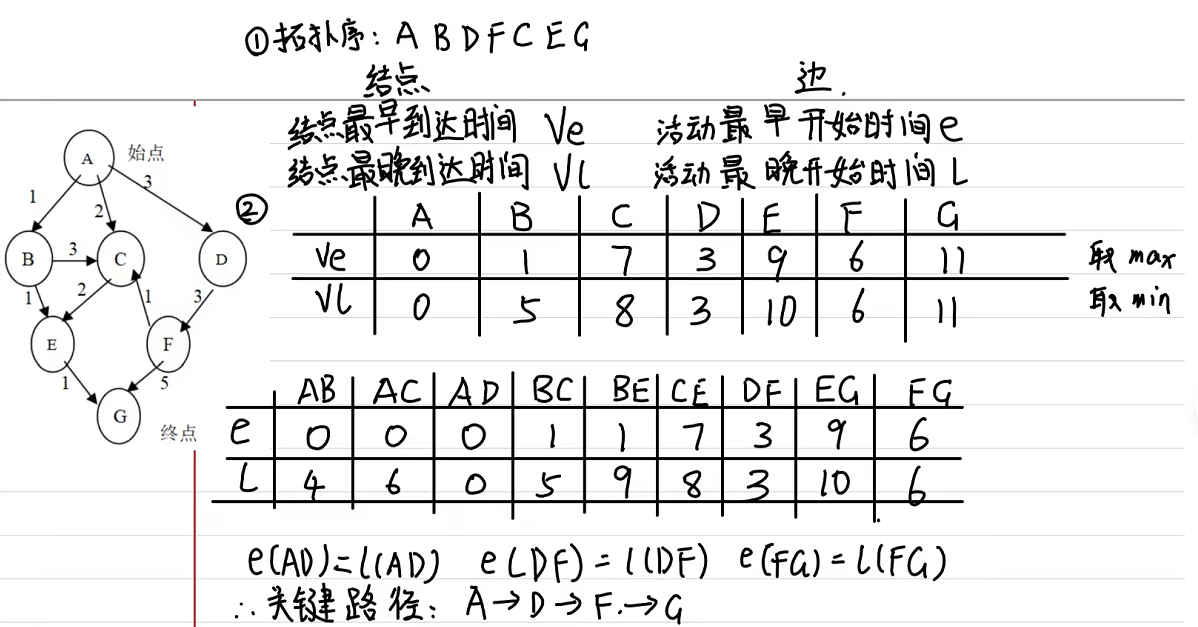
Ve表示，每个结点最早的开始时间，Vl表示每个结点最晚的开始时间，e表示每条**边（互动）**最早的开始时间，l表示每条边最晚的开始时间

首先计算Ve，从起点开始（题中A），时间定为0，然后进入下一个结点B，其Ve值是所有进入这个点的边中，边的起点Ve值加上这条边的权值的和，最大的那个值作为结点B的Ve值。

然后计算Vl，从终点开始，我们经过上一步知道到达终点的Ve值，那么初始化终点的Vl值为这个Ve值，然后进入下一个结点C时，这个点的Vl值，是从这个点出发且边的终点Vl值减去边权的差的值最小的那个值，作为C的vl值。

在计算玩vl值和ve值后可以计算e值和l值，e值为当前边的起点的ve值，l值为当前边的终点的vl值减去边权。在计算完毕后，e值和l值相同的边为关键路径。

查找

二叉排序树和二叉平衡树

二叉排序树（排序二叉树）：满足左比他小，右比他大就行

二叉平衡树（平衡二叉树）：满足二叉排序树的要求下，任意一个节点的左子树深度与右子树深度之差的绝对值不大于1

B-树

一棵m阶的B-树，或为空树，或为满足下列特征的m叉树

树中每个结点至多有m棵子树
若根结点不是叶子结点，则至少有两棵子树
除根之外的所有非叶子结点至少有 $\lceil \frac m2 \rceil$ 棵子树
所有的叶子结点都出现在同一层次上，并且不带信息，通常称为失败结点。失败结点并不存在，指向这些结点的指针为空。引入失败结点是为了便于分析B-树的查找性能
所有的非叶子节点最多有m-1个关键字

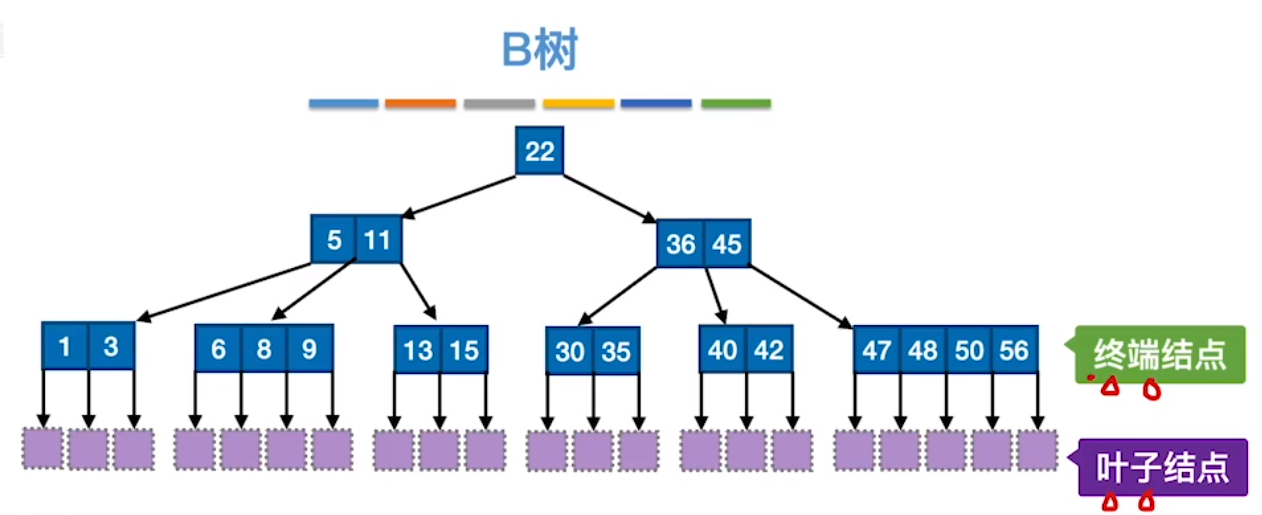
n个关键字的m阶B树有，其高度h满足 $log_m(n+1)\leq h \leq log_{\lceil \frac m2 \rceil} \frac{n+1}2+1$

n个关键字的B树必有n+1个叶子节点

B树的插入

插入一个节点的时候，先要找到对应的位置（最底层的终端节点），如果插入位置插入后超出了B树的限制，则需要从这个节点的中间（ $\lceil m/2 \rceil$ ）取出元素，移动到上一层的节点中，然后将后面剩下的部分进行分裂，如果移动到上一层的节点也超出了限制，则也是找到中间的节点，上移，然后分裂

B树的删除

若删除的是终端节点则直接删除即可

如果不是终端节点，那么就对当前节点的左指针指向的子树中，最右边的终端节点，替换当前的位置

或者使用当前节点的右指针指向的子树中，最左边的终端节点，替换当前的位置

如果删除了终端节点前后，这个节点的数量少于下限

如果右兄弟借一个还够的话，可以将这个节点的父亲数据拿下来，然后用右兄弟节点中的第一个数据顶上
如果有兄弟不够借但是左兄弟够借的话，可以将这个节点的父亲数据拿下来，然后用左兄弟的最后一个数据顶上
如果左右都不够借了，就将这个节点的父节点加到这里来，然后取右兄弟的所有点都加入到这个点中，如果这造成了父节点那一层数据低于下限，则按照合并规则继续合并

排序

假设有个系统要多次对n个关键字进行排序，n很大且每次排序时关键字的分布情况不明。系统不希望每次排序时间变动过大，而且希望越快越好，哪种排序算法较好？为什么？

堆排序算法较好。首先，因为堆排序平均时间复杂度为O(nlogn)，性能较好；另外，因为关键字分布情况不明，堆排序最坏时间复杂度为O(nlogn)，保证计算时间不会出现O(n2)而造成很大的延迟，此时，快速排序算法不太合适。此外，堆排序只需要O(1)个辅助空间，归并排序虽然总体性能也很不错，也满足系统的要求，但需要O(n)的辅助空间。