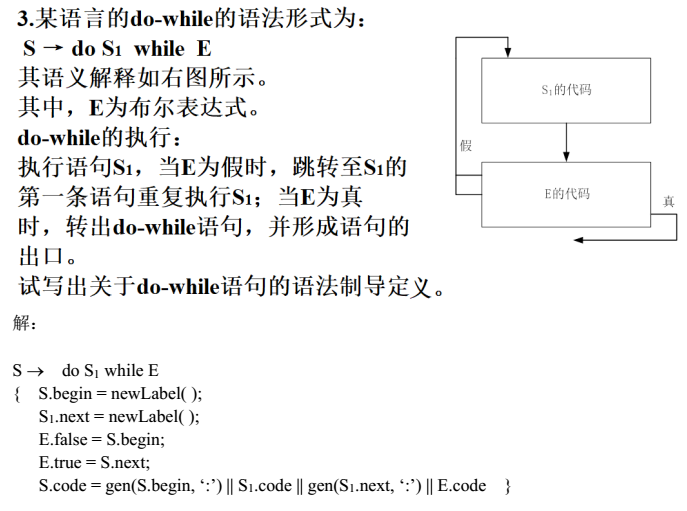
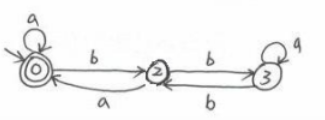
「编译原理」编译原理习题类型
编译阶段
给出可能出错的代码,或者出错的方式,询问是在编译的哪个阶段会发生报错
比如:
1 | // c代码 |
- 在词法分析阶段报错
- 在语法分析阶段报错
- 在语义分析阶段报错(其还包括调用未定义的函数)
词法分析
状态转换图的接收与拒绝
比如下图:
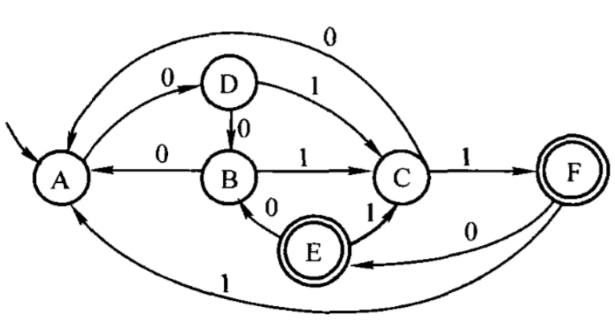
图中一开始有箭头(出发端没有元素)指向的状态为初态(图中A),有两层圈的状态为终态(图中E,F)。
对于任意一个输入串,比如011,其满足从初态出发,在经过对应字符的遍历A->D->C->F后,到达终态(即最后一个点为终态)则可以接收这个输入串,反之(最后一个点不是终态)则不可以接收
状态转化矩阵
比如:
| 状态 | a(对应第一列状态的情况下输入a) | b(对应第一列状态的情况下输入b) |
|---|---|---|
| S | A | S |
| A | A | B |
| B | B | B |
初态:S,终态:B
矩阵表示的当处于S状态时,当接收a时,下一个状态为A,当接收b时,下一个状态S。其他同理,根据合格规则可以绘制出状态转换图。初态和终态在给出状态转化矩阵时,一般都会直接给出。
正规式(正则表达式)运算符的优先级
NFA的确定化
比如下图:
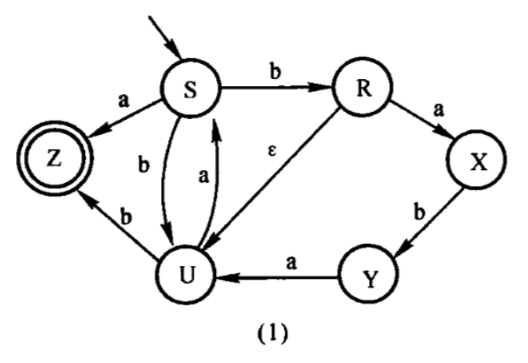
这种题型包括两种类型,一种是带和不带的。
两者区别就在于如果是带的类型就需要先计算每个状态的(空闭包),不带可以跳过(因为不带的就是状态自己本身)
这题首先要计算
| 状态 | |
|---|---|
| {S} | {S} |
| {R} | {R,U} |
| {X} | {X} |
| {Y} | {Y} |
| {U} | {U} |
| {Z} | {Z} |
并且可以确定初态为S,终态为Z
然后使用S初态的空闭包作为DFA最初的元素,然后根据输入的不同符号,确定其可以到达的下一个状态集合,并对状态集合中的每一个元素的空闭包求一个并集,作为最终状态。如果产生了新的状态,就根据这个新的状态,按照输入的符号判断下一个状态,如果又产生了新的状态就重复之前的操作,直至没有新的状态产生。于是可以得到状态转换矩阵(其中我用Q对新状态进行重命名)
举个例子:
S输入b后可以到达的下一个状态为{R,U},对这两个状态的空闭包取一个并集,即{R,U}并{U} = {R,U},这个就是S输入b后在DFA中最终到达的状态
| 状态 | a | b |
|---|---|---|
| Q1 = {S} | {Z}=Q2 | {R,U}=Q3 |
| Q2 = {Z} | ||
| Q3 = {R,U} | {X,S}=Q4 | {Z}=Q2 |
| Q4={X,S} | {Z}=Q2 | {Y,U,R}=Q5 |
| Q5={Y,U,R} | {U,S,X}=Q6 | {Z}=Q2 |
| Q6={U,S,X} | {S,Z} = Q7 | {Z,R,U,Y}=Q8 |
| Q7={S,Z} | {Z}=Q2 | {R,U}=Q3 |
| Q8={Z,R,U,Y} | {X,S,U}=Q6 | {Z}=Q2 |
这是DFA的状态转化矩阵,然后是要确定初态和终态,首先初态就是NFA中的初态的空闭包元素(Q1),而在NFA中的终态是Z,那么在DFA中包含Z的状态都是终态(Q2,Q7,Q8)
(ps,图我就不画了,反正按着上面的矩阵画就不会错了,考试的时候一定要画图)
DFA最小化
如下图:
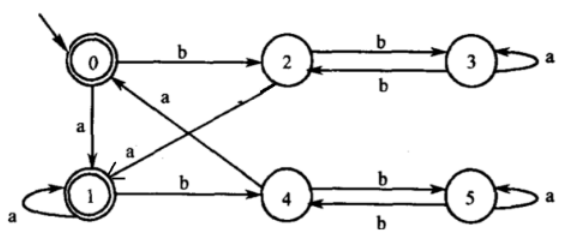
首先将图中的状态集合按照是否为终态划分成两部分,称为,然后检查每个被拆分的集合中,是否还有可分的元素。解决过程如下
因为不可区分,所以先不处理
因为可以区分,所以被拆分为
于是生成新的状态集合
因为,不可区分,所以不处理
因为,不可区分,所以不处理
最后的结果为:
然后将对应的状态进行合并就行,结果如下图
正规式与NFA的互相转化
转化规则为:

在转化成NFA时,优先做优先级低的操作,即选择->链接->闭包
NFA转成正则式,也用相同的规则就行了
比如将正规式构造成NFA过程如下:
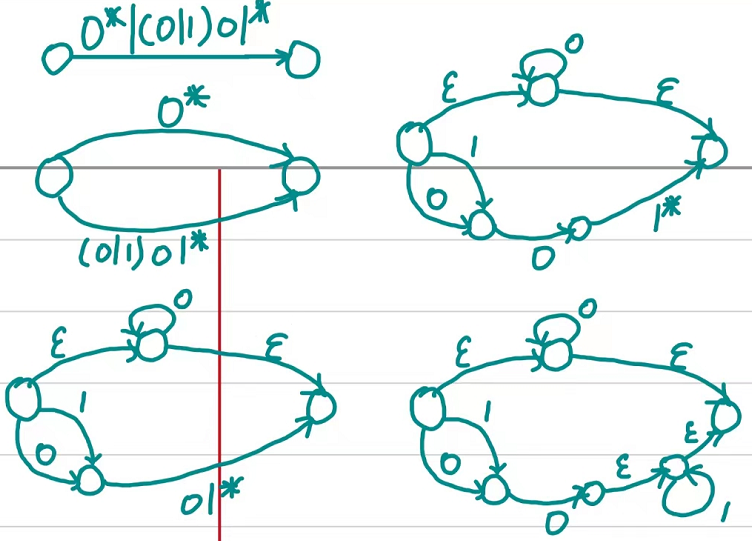
语法分析
文法的分析树,最左推导,最右推导(规范推导)
文法树:按着文法以树的方式展开成对应的句子
最左推导:优先满足最左端符号的匹配,按照文法展开成对应的句子
最右推导:优先满足最右端符号的匹配,按照文法展开成对应的句子。

文法二义性
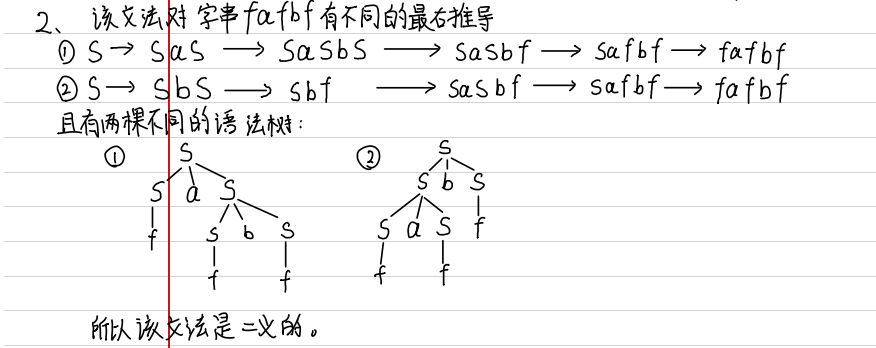
证明一个文法存在二义性,只需要找到一个句子,他有两棵不同的语法树(或者两种不同的最左,最右推导)。
已知文法G[S]:S->SaS|SbS|cSd|eS|f,证明该文法是二义的:
(ps:我这里写了两种方式,但其实只用写出推导或者语法树就可以了)
FIRST集与FOLLOW集
FIRST集和FOLLOW集,针对的都是非终结符
假设要求S的FIRST集,首先需要看一下所有左边是S的推导式,然后找出右边第一个符号,如果是非终结符,那么他就是FIRST集的元素之一,如果他是非终结符,那么还要按照相同的方法,先找出这个非终结符的FIRST集,然后将FIRST集作为S的FIRST集元素(和本身自己的取并集),如果非终结符可以得到,那么还要跳过这个非终结符往后看一下是终结符还是非终结符,然后同上操作,FIRST是带不带的
假设要求S的FOLLOW集,先给文法起始点的follow集添加一个符,然后要找出所有推导式右边存在S的推导式,然后看S的右边一个元素是什么,如果是终结符,他就是S的FOLLOW集之一,如果是非终结符则这个非终结符的FIRST集中非空的部分也是S的FOLLOW集之一,如果这个非终结符可以表示则再向后看一个符号,同上操作。如果S的后面没有符号了,那么这个推导式左边元素的FOLLOW集也是S的FOLLOW集之一。FOLLOW集是带不带的
LL(1)文法
判断是否为LL(1)文法的方法:
- 不存在左递归
- 对于所有的非终结符,其可以选择的所有转化方式的FIRST集(如果可以转化为,则使用非终结符的FOLLOW集)相交的结果为
举个例子:
已给文法 S->SaB S->bB A->S A->a B->Ac
- 这个文法是不是LL(1)文法,如果是请构造LL(1)文法分析表,如果不是,请将其改造成LL(1)文法,然后写出文法分析表
- 并给出句子bac的分析过程
-
不是LL(1)文法,因为该文法存在左递归,消除左递归后的文法为:
-
然后计算这些推导式的FIRST和FOLLOW集
-
对于,在S在左边的所有推导式中,右边第一个字符的集合为,所以
对于,在在左边的所有推导式中,右边第一个字符的集合为,所以
对于,在在左边的所有推导式中,右边第一个字符分别为S,和a,那么a一定是的一个元素,对于非终结符S,其FIRST集也是的元素,所以
对于,在B在左边的所有推导式中,右边第一个字符为A,那么中的元素,一定是中的元素,所以
-
首先给初始的推导式添加一个符号,即,然后在S在右边的所有推导式中,S的右边是空的,那么可以得到
然后计算,在A在右边的所有推导式中,A的右边一个元素是c,那么c就是的元素之一,然后后面没有A在右边的推导式了,所以,所以
然后计算,在在右边的所有推导式中,对于第一项,因为的右边为空,所以是的元素之一,在第二项中,的右边也为空,所以也是元素之一,所以
最后计算,在B在右边的所有推导式中,B的右边为,所以应该为的元素,然后由于有,所以会有新的产生式,此时B的右边是空,所以应该也是的元素,所以
-
为了方便查看,画一个表吧
非终结符 FIRST FOLLOW S b A a,b c B a,b -
然后需要验证这个改造后的文法是不是LL(1)文法,首先对所有有不同推导结果的非终结符,每个终结符在自己可选择的内容中的FIRST的交集(如果是求变换成这个非终结符的FOLLOW集)必须为空,即
因为交集都是空,所以这个文法是LL(1)文法
-
写出文法分析表,文法分析表从左边的终结符出发,然后看看他的FIRST集有哪些,然后FIRST集中的元素可以对应到终结符的推导式中,将其填入表中,如果是则要看他的FOLLOW集,FOLLOW集对应的非终结符和终结符对应的格子,就是填终结符转化成的格子,如下表
非终结符 a b c S A B -
最后就是对给定的句子进行分析,首先把初态放入分析栈中,句子放入输入缓冲区并添加一个,然后根据输入缓冲区碰到的最左边的元素决定使用哪条产生式,然后将分析栈中的元素出栈,将产生式右边的部分按从y右到左的方式入栈,然后继续匹配,如果匹配成功,就直接将缓冲区和栈中的字符弄出去。直到分析栈和输入缓冲区都只剩下,如果按照分析表遇到空的情况则分析失败。题目分析结果如下表
步骤 分析栈 输入缓冲区 输出产生式 1 2 匹配b 3 4 5 匹配a 6 匹配c 7 8 匹配成功
LR(0)文法
判断是否是LR(0)文法的方法:查看所生成的识别活前缀的DFA中,是否存在移进规约冲突(即一个状态既存在移进又存在规约)。
注意:LR系列的文法都不需要消除左递归,只有LL需要消除左递归
举个例子:
设已给文法G[S]:S->aSb,S->aSc,S->ab
- 构造他的识别全部活前缀的DFA
- 构造LR(0)分析表
- 给出LR(0)分析表对输入符号串aaabcb的分析过程
-
首先需要对文法进行拓展,需要添加一条,结果如下:
-
然后开始构造识别活前缀,首先取出0的产生式,然后在其右部的最左边写上一个的标记,然后查看这个标记的右边是否是非终结符,如果是的话这个状态就结束了,不然就需要将左部是这个非终结符的产生式全部写入状态中,然后在产生式右边的最左边写上标记,直至不再有新的非终结符出现,然后根据记号右边的一个元素,对这个状态进行输入,然后产生的新的状态的这个产生式的记号,向右移动一个字符,按照之前的方法构建这个状态。然后按照相同的方法生成新的状态,直至不再产生新的状态(标记移动到产生式右部的最右边就不会再移动了)。题目的结果如下图所示:

-
然后根据这个DFA构造LR(0)分析表,分析表分为两个部分,action(终结符输入),goto(非终结符输入)。从0状态出发,观察0状态可以接收的输入符号,然后跳转到对应的下一个状态中,或者使用生成式进行规约(规约就用对应的产生式填完一行的ACTION部分就行)。当拓展出的产生式标记到达最右边时,说明这个输入串可以被接收。分析表构建如下
状态 ACTION GOTO a b c S 0 1 1 acc 2 3 3 4 5 6 -
分析符号串aaabcb,把和初始状态放入到分析栈中,句子带上,放入余留输入串中,然后根据栈顶状态和余留输入串的第一个字符,判断移进和规约操作,并确定下一个状态,如果是移进将字符和状态分别放入分析栈中,然后进行下一轮分析。如果是规约的话,就按照产生式,将右部有的符号全部出栈,然后根据剩下的栈顶状态,配合产生式左部的非终结符判断下一个状态应该goto到哪个状态。如果碰到表格中空白的地方,就直接分析失败,如果碰到了ACC就是分析成功,分析过程如下表
步骤 分析栈 余留输入串 分析动作 下一状态 1 移进 2 2 移进 2 3 移进 2 4 移进 4 5 规约 GOTO(2,S)=3 6 移进 6 7 规约 GOTO(2,S) = 3 8 移进 5 9 规约 GOTO(0,S)=1 10 分析成功
SLR(1)文法
这个文法尝试使用FOLLOW集的方式解决移进规约冲突的问题,即如果一个状态出现了规约和移进,那么规约后生成的非终结符的FOLLOW集与移进接收的符号没有交集,则可以解决冲突,这个解决冲突的方案就是SLR(1),就是解决冲突的地方不一样,其他和LR(0)基本一致。
举个例子:
已知文法G[S]:
(1):S->Pa (2): S->Pb (3):S->C (4): P->Pd (5): P->Se (6)P->f
判断文法G[S]分别是LR(0)和SLR(1)文法吗?为什么?若G[S]是LR(0)文法,请构造其相应的LR(0)的分析表,若G[S]是SLR(1)文法,请构造其相应的SLR(1)的分析表
-
首先要添加一个拓展文法(0): S’ ->S
-
然后尝试画出他的识别活前缀DFA(过程和LR(0)一致),结果如下图所示:
-
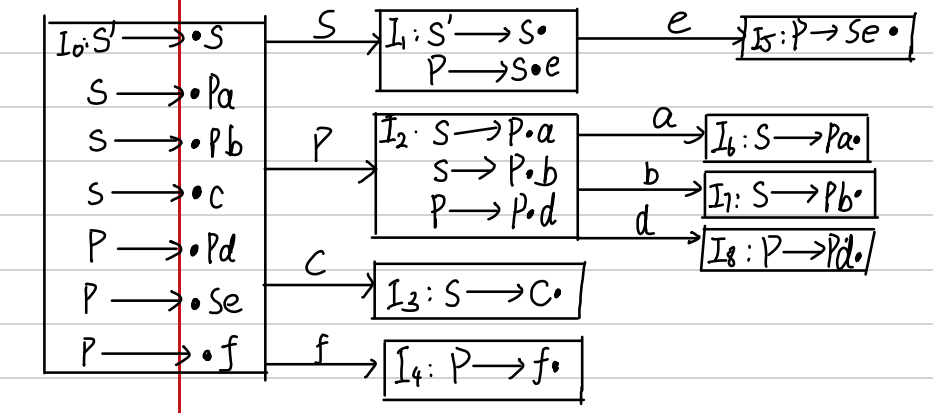
-
从图中可以看出,I1状态存在移进规约冲突所以不是LR(0)文法,然后按照之前说的,看看移进所需的字符和FOLLOW(S’)是否有交集(FOLLOW集的求解我就不具体写了,详细可以去之前的内容看看),那么,所以冲突可以被解决,这是一个SLR(1)文法
状态 FOLLOW S P a,b,d -
然后绘制SLR(1)分析表,绘制过程对于移进的地方基本一致,但是规约的地方不一样了,对某个非终结符的规约,会选择这个非终结符和这个非终结符对应的FOLLOW集指向的格子填写规约。结果如下表
状态 ACTION GOTO a b c d e f S P 0 1 2 1 acc 2 3 4 5 6 7 8 (如果还有分析句子的话,分析过程按照表来然后过程和LR(0)完全一致)
LR(1)文法
LR(1)文法是在SLR(1)上的进一步拓展,如果使用FOLLOW集无法解决移进规约规冲突,则可以在生成活前缀中尝试引入第二分量,对于一开始引入的拓展文法,他的第二分量就是,然后如果有新的非终结符引入新的产生式,那么他的第二分量就根据其来源的地方的右边字符,如果字符是终结符就直接作为第二分量,否则则是非终结符的first集,如果非终结符可以为空还要再分析一下
举个例子:
已知文法G[Z]:
(1)Z->Aa (2)Z->bAc (3)Z->dc (4) Z->bda (5) A->d
判断文法G[Z]是SLR(1)文法吗?为什么?若不是SLR(1)文法,可以用什么分析法对文法G[Z]产生的语言进行有效的分析,并给出其分析表
-
不是SLR(1)文法,因为项目集存在移进规约冲突,且与的交集为,因此文法G[Z]不是SLR(1)文法,对文法G[Z]产生的语言可以使用LR(1)分析法进行有效分析。(ps:这里的项目及主要就是使用之前的构造方式构造了DFA然后找出冲突项然后分析,这里就不详细展开了)
-
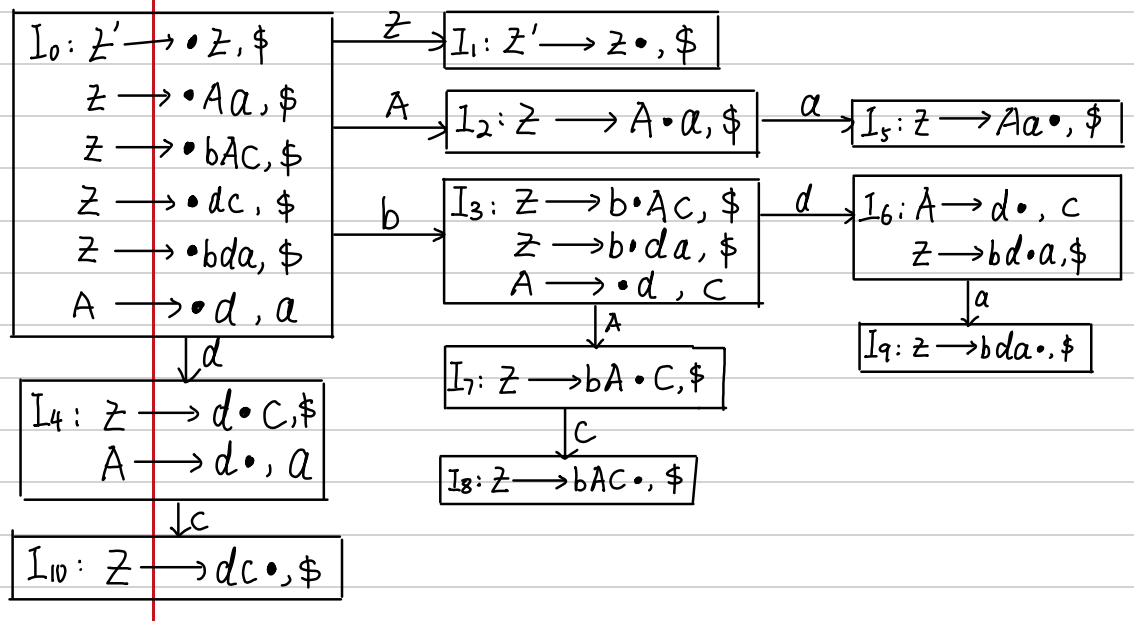
LR(1)文法,仍然要先进行拓广文法:(0)Z’->Z,并获得识别活前缀的DFA(带有第二分量),如下
-
构造分析表的时候,正常写就是按照接收的字符串来,只有在规约的时候与SLR(1)有点不一样,在规约的时候,是根据第二分量的符号来确定是否进行规约,分析表如下表
状态 ACTION GOTO a b c d Z A 0 1 2 1 acc 2 3 7 4 5 6 7 8 9 10 -
分析句子也是和之前的方式一样
中间代码生成
语法制导翻译
两种类型,一个是已知翻译方式,求句子翻译的输出结果,另一个是已知句子翻译的输出结果,找到文法的翻译方式。
举个例子:
文法G[S]及相应的翻译方案如下:
S->bAb {print:“1”}
A->cB {print:“2”}
A->a {print:“3”}
B->Aad {print:“4”}
输入串为bcaadb时,该翻译方案的输出是什么?
首先画出这个句子的语法树,然后按照最左规约的方式在句子进行规约的顺序进行标号,当完成规约后直接输出规约方式对应的翻译内容即可。

举个例子:
已知文法G[D]:
D-> int id | real id | D1, id
请你将其翻译,使其能够统计一共说明了多少个变量

算术表达式转化
- 转化成语法树的形式
- 转化成有向无环图DAG的形式
- 转化成后缀表达式(逆波兰式)
- 三地址代码
举个例子:
把算数表达式翻译成语法树,有向无环图DAG,后缀表达式,三地址代码
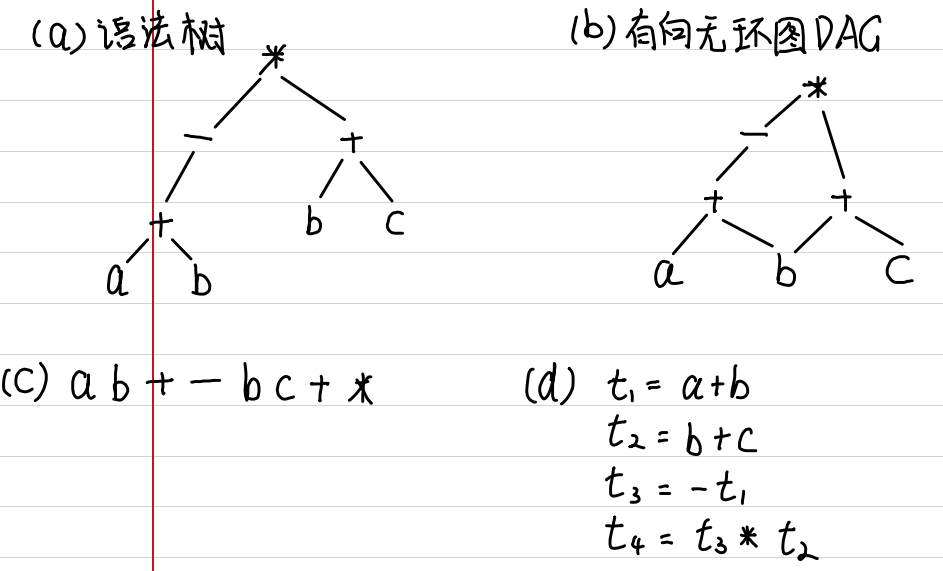
三地址代码转化
需要根据下面的控制流语句的翻译图进行(if-then-else语句中如果then的部分被嵌套在while里,他除了回到while的判断状态,还要goto到if结束的状态,不要问为什么,问就是和课本保持一致,反正图中的深蓝色的部分要特别注意)
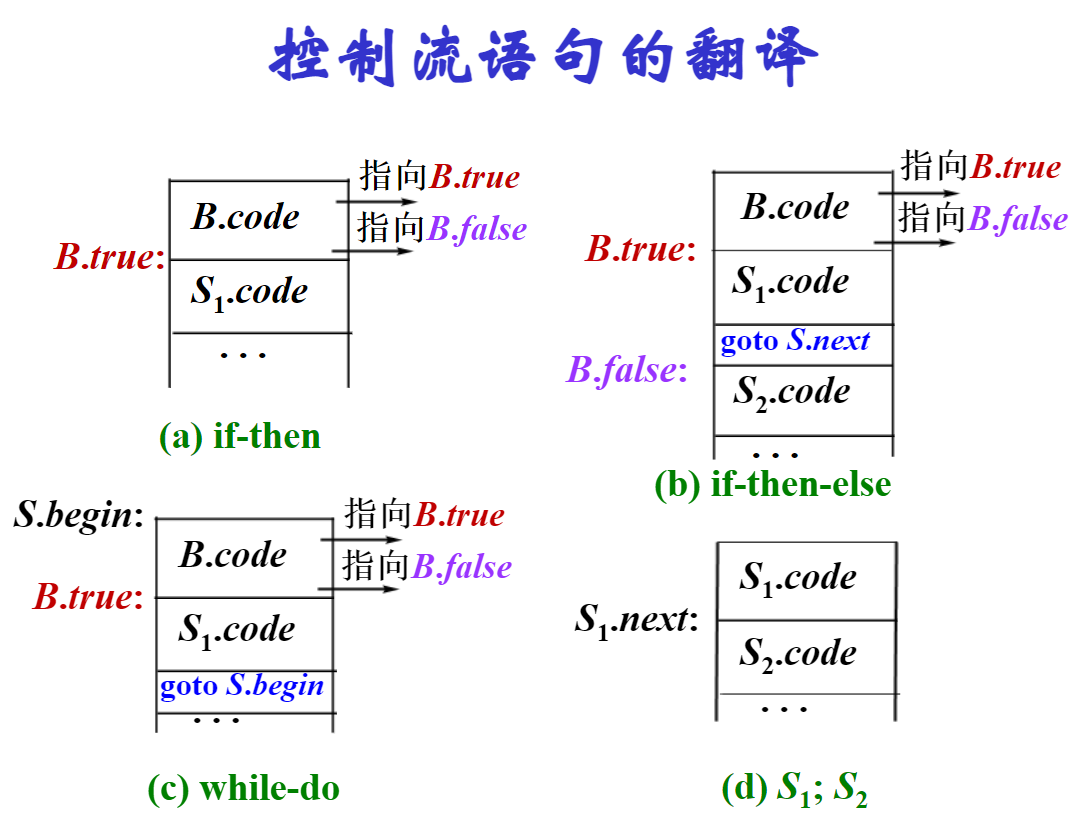
举个例子:
请将下面的语句翻译成三地址代码:
if (z<x) or (z>y) then
while(x>y) do a = a+1;
else a = a-1;
x = y+z;
先把代码换成更直观的转化图(稿纸上做),然后开始翻译三地址代码,注意红框的部分,就是为了和教材翻译过程一致(if的then后面要加一个goto表明他结束后要去哪里),虽然并没有什么用,但是一定要加(至少我学校是这样的)。
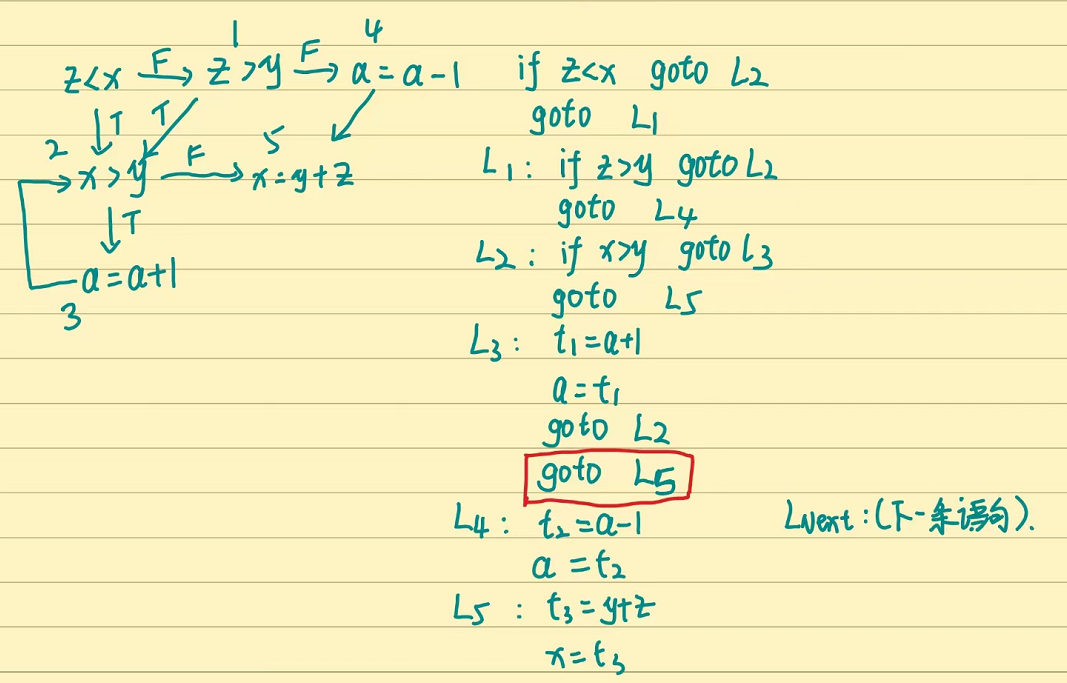
不太懂的东西