「论文阅读」Visual Object Tracking using Adaptive Correlation Filters

论文名称：Visual Object Tracking using Adaptive Correlation Filters

作者：David S. Bolme; J. Ross Beveridge; Bruce A. Draper; Yui Man Lui

时间：2010-7

期刊：CVPR2010

Origin Abstract

Although not commonly used, correlation filters can track complex objects through rotations, occlusions and other distractions at over 20 times the rate of current state-of-the-art techniques. The oldest and simplest correlation filters use simple templates and generally fail when applied to tracking. More modern approaches such as ASEF and UMACE perform better, but their training needs are poorly suited to tracking. Visual tracking requires robust filters to be trained from a single frame and dynamically adapted as the appearance of the target object changes.

This paper presents a new type of correlation filter, a Minimum Output Sum of Squared Error (MOSSE)filter, which produces stable correlation filters when initialized using a single frame. A tracker based upon MOSSE filters is robust to variations in lighting, scale, pose, and non-rigid deformations while operating at 669 frames per second. Occlusion is detected based upon the peak-to-sidelobe ratio, which enables the tracker to pause and resume where it left off when the object reappears.

Abstract

虽然不常用，相关滤波可以通过旋转，遮挡和其他干扰来跟踪复杂的物体，其速度是SOTA的20倍以上。最古老和最简单的相关滤波使用简单的模板，在应用于跟踪时通常会失败。更现代的方法，比如ASEF和UMACE表现更好，但是他们的训练需求不太适合跟踪。视觉跟踪要求鲁棒的滤波器从一个单一的帧训练和动态适应目标物体外观的改变。

这篇论文提出了一个新型的相关滤波，一种平方误差最小输出和（MOSSE，Minimum Output Sum of Squared Error）滤波器，他在单帧初始化时产生稳定的相关滤波器。基于MOSSE滤波器的追踪器，在699的帧率下，对光线，尺寸，姿势以及非刚性变化具有很好的鲁棒性。遮挡(Occlusion)的检测是基于peak-to-sidelobe率的，这使得追踪器会暂停，并在对象重新出现的时候，恢复原来的状态。

Introduction

视觉跟踪在视频处理中有许多实际应用。当目标位于视频的一帧中，在后续帧中跟踪该目标通常是有用的。成功跟踪目标的每一帧都提供了关于目标身份和活动的更多信息。由于跟踪比检测更容易，对比与运行一个目标检测在每一帧，跟踪算法可以使用更少的计算资源。

今年来，视觉跟踪收到了广泛的关注。提出了一些能够容忍目标外观变化并通过复杂运动跟踪目标的鲁棒跟踪策略。最近的例子包括：增量视觉跟踪（IVT），鲁棒基于片段的跟踪（FragTrack），基于图的鉴别学习（GBDL）以及多实例学习（MILTrack）。尽管有效，但这些技术并不简单，他们往往包括复杂的外观模型和优化算法，因为难以跟上许多线代相机产生的25-30帧/每秒。这个如下表所示：

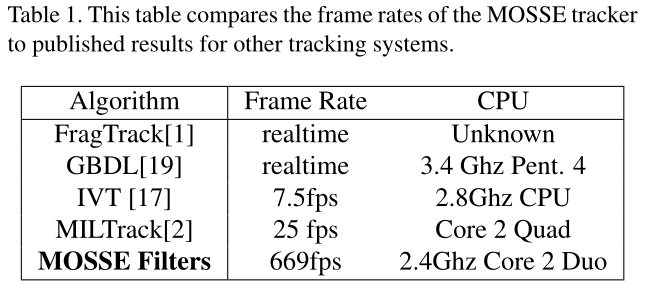
表1：表格比较了不同帧率的MOSSE跟踪器去得到其他跟踪系统的结果

在本文研究了一种简单的跟踪策略，采用自适应相关滤波器对目标外观进行建模，通过卷积进行跟踪。采用自适应相关滤波对目标外观进行建模，通过卷积进行跟踪。创建滤波器的幼稚方法（Naive method），如从图像中裁剪模板，会为目标产生强烈的峰值，但也会对背景做出错误的相应。因此，他们不是特别鲁棒的目标外观变化和失败的挑战性跟踪问题。综合精确滤波器(ASEF)的平均值，无约束最小平均相关能量(UMACE)和最小误差平方世初和(MOSSE)产生的滤波器对外观变化具有更强的鲁棒性，能更好地区分目标和背景。如下图所示，结果是一个更强大的峰值转化为更少的偏移(drift)和更少的下降追踪(fewer dropped tracks)。传统的ASEF和UMACE，滤波器是离线训练的，用于目标检测或目标识别。在这项研究中，作者修改了这些技术，以在线训练和一个自适应的manor视觉跟踪，没太看懂这句：In this research, we have modified these techniques to be trained online and in an adaptive manor for visual trackin（在这项研究中，作者修改了这些技术，从而以一种自适应的方式实现在线训练，并应用于视觉跟踪）这个方法实现了跟踪的SOTA性能，其保留了相关性方法的大部分速度和简单性。

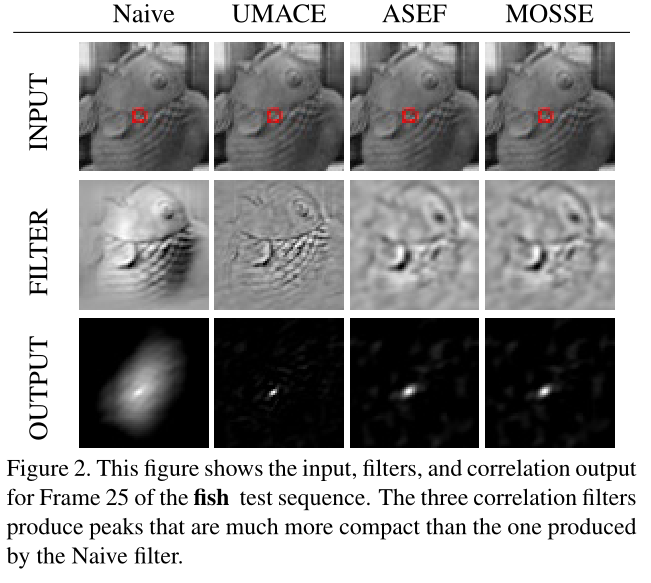
图2：这张图展示了对25帧的鱼测试序列的输入，滤波器，相关性输出。这三个相关性滤波器产生的峰值比单纯滤波器产生的峰值要紧凑得很多。

尽管这都是简单的方法，但是在旋转，缩放，光照和部分闭塞（partial occlusion）的改变下，基于ASEF,UMACE或MOSSE滤波器的追踪器表现很好。用于度量相关峰值强度的Peak-toSidelobe率(PSR)，被使用去检测遮挡或者跟踪故障，停止在线更新，并重新获取跟踪器，如果对象出现类似的外观。更一般地说，这些先进的相关滤波器的性能与前面提到的更复杂的跟踪器一致，但是，基于滤波器的方法速度快20倍，可以处理669的帧率。

SDF：综合判别函数(Synthetic Discriminant Functions)

MVSDF：最小方差综合判别函数(Minimum Variance Synthetic Discriminant Functions)

OTF：最佳折衷滤波器（Optimal Tradeoff Filters）

MSESDF：最小平方误差综合判别函数(Minimum Squared Error Synthetic Discriminant Functions)

ASEF：综合均值提取滤波器( Average of Synthetic Exact Filters)

UMACE：无约束最小均值相关能量(Unconstrained Minimum Average Correlation Energy)

MOSSSE：平方误差最小输出和 (Minimum Average Correlation Energy)

Correlation Filter Based Tracking

基于滤波器的跟踪器利用对实例图像训练的滤波器对目标的外观进行建模。首先根据以第一帧中的物体为中心的小跟踪窗口选择目标，从现在开始，跟踪和过滤训练一起工作。通过下一帧中搜索窗口上的相关滤波器来跟踪目标，相关输出中与最大值对应的位置表示目标的新位置，然后根据该新位置执行在线更新。

为了创建一个快速跟踪器，相关性是在傅里叶域进行了快速傅里叶变换(FFT)。首先，计算输入图像 $F=\mathcal{F}(f)$ 和滤波器 $H=\mathcal{F}(h)$ 的2D傅里叶变换。卷积理论表明相关性就是在傅里叶域的一个element-wise乘法。使用 $\odot$ 符号表示element-wise 乘法，使用 $*$ 去表示复共轭，相关性表现为：

$公式1：G=F \odot H^{*}$

使用反快速傅里叶变换，相关输出被转换回空域。这个过程的瓶颈在于反向和正向FFT的计算，这样整个过程的时间上限是 $O(P \log P)$ ，其中P是在跟踪框中像素的数量。

Preprocssing

FFT卷积算法的一个问题是将图像和滤波器映射到环面（torus）的拓扑结构。换句话说，它连接了图像的左边界和右边界，把顶部和底部链接起来。在卷积中，图像通过环形空间(toroidal space)旋转，而不是像在空间域中那样平移。人为地连接图像的边界会引入一个影响相关输出的假象(artifact)。这种假象可以使用预处理进行解决。首先像素值转化时使用log函数，这有助于低对比度照明的情况。将像素值标准化为均值为0，方差为1，最后，将图像乘以余弦窗口(cosine window)，余弦窗口逐渐将边缘附近的像素值减少到0。他把更多的终点放在目标的中心附近。

MOSSE Filters

MOSSE是一种从较少的训练图像生成类似ASEF的滤波器算法。首先，他需要一组训练图像 $f_i$ 和训练输出 $g_i$ 。通常 $g_i$ 可以是任何形状。在这种情况下，在训练图像 $f_i$ 的目标中心，由ground truth生成的 $g_i$ 具有紧凑的$\sigma=2.0$2D高斯形状的峰，这个峰的中心位置为目标。

训练是在傅里叶域进行的，以利用输入和输出之间简单的element-wise关系。将大写的变量 $F_i,G_i$ 和滤波器 $H$ 定义为小写变量的傅里叶变换，如下公式所示：

$公式2：H_{i}^{*}=\frac{G_{i}}{F_{i}}$

为了找到将训练输入映射到所需训练输出的滤波器中，MOSSE找到一个滤波器H，最小化卷积的准确输出与卷积期望输出之间的平方误差和。这个最小化问题任务可以表示成：

$公式3：\min _{H^{*}} \sum_{i}\left|F_{i} \odot H^{*}-G_{i}\right|^{2}$

最小化输出的平方误差和的想法并不新鲜。在这些工作中，假定目标总是在 $f_i$ 的中心，并且输出 $(g_i)$ 对于整个训练集是固定的，而定制每个 $g_i$ 是ASEF和MOSSE背后的基本思想。在跟踪问题中，目标不是一直在中心的，并且 $g_i$ 中的峰值跟随 $f_i$ 中的目标移动。在更一般的情况下 $g_i$ 可以由任何形状。

解决这个最优化问题并不特别困难，但是需要一些注意，因为函数被优化是一个复杂变量的实值函数(a real valued function of a complex variable)。首先，由于傅里叶域中的所有运算都是element-wise的，H的每个元素(以 $\omega$ 和 $\nu$ 为索引)都可以独立求解。这设计到根据 $H_{\omega\nu}$ 和 $H_{\omega\nu}^{*}$ 重写函数。然后，部分提到的 $H_{\omega\nu}^*$ 设置为0，而 $H_{\omega\nu}$ 被当做一个独立的变量。

$公式4：0=\frac{\partial}{\partial H_{\omega \nu}^{*}} \sum_{i}\left|F_{i \omega \nu} H_{\omega \nu}^{*}-G_{i \omega \nu}\right|^{2}$

通过对 $H^*$ 的求解，得到了MOSSE滤波器的闭式（close form）表达式

$公式5：H^{*}=\frac{\sum_{i} G_{i} \odot F_{i}^{*}}{\sum_{i} F_{i} \odot F_{i}^{*}}$

公式5中的terms(术语)有一个又去的解释，分子是输入和期望输出之间的相关性，分母是输入的能量谱。

从公式5，我们可以简单展示UMACE是一种特殊的MOSSE，UMACE中定义 $H^*=D^{-1}m^*$ ，其中m是一个包含平均中心裁剪训练图像的FFT向量。 $D$ 是一个包含训练图像的平均能量谱的对角矩阵。因为D是一个对角矩阵，因此乘上他的逆可以表示为一个element-wise的除法。用当前符号重写时，UMACE可以表示为：

$公式6：H^{*}=\frac{\sum_{i} F_{i}^{*}}{\sum_{i} F_{i} \odot F_{i}^{*}}$

然而，UMACE需要在 $F_i$ 的中心，重定位(recentering)可以使用相关性来执行，如果我们定义 $g_i$ 为一个Kronecker delta(目标中心的峰值为1，其他地方的峰值为0)，这实际上将重新定位目标并计算UMACE filter。这与传统实现的不同之处在于，这里我们先进行裁剪，然后再进行转换，传统方法在这里先进行转换，然后在进行裁剪。

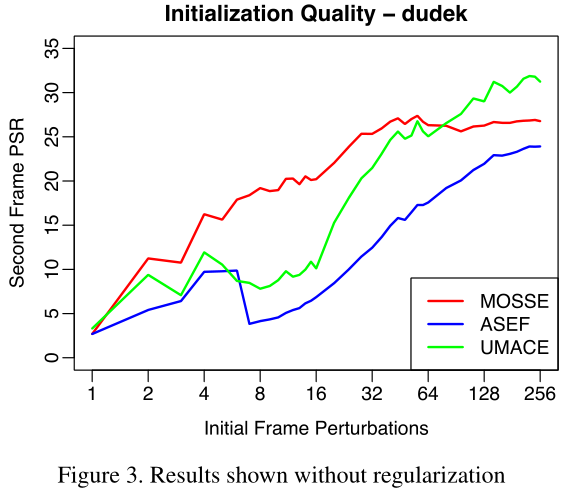
为了证明MOSSE比ASEF能够产生更好的滤波器，作者进行了一项实验，改变了用于训练滤波器的图像数量。通过对视频第一帧的跟踪窗口施加随机小仿射扰动（random small affine perturbations）来初始化滤波器。在第二帧的PSR被用于度量滤波器的质量。下图展示了MOSSE在少数几个图像窗口上训练时会产生更好的滤波器。

Regularization of ASEF

ASEF采用了稍微不同的方法去最小化相对性转化的误差。结果是，当只有一张训练图像 $F_i$ 和一张输出图像 $G_i$ 时，存在一个滤波器，产生0误差。这个滤波器被称为精确(exact)滤波器，并可以通过求解公式1得到：

$公式7：H_{i}^{*}=\frac{G_{i}}{F_{i}}=\frac{G_{i} \odot F_{i}^{*}}{F_{i} \odot F_{i}^{*}}$

在一张图上训练的精确滤波器总是过拟合这张图，当应用到一张新的图上时，这个滤波器通常会失效。用平均来生成滤波器会更加通用(Averaging is used to produce a filter that is more general)。使用平均的动机来自Bootstrap Aggregation，其中弱类别的输出可以被平均来产生一个更强大的分类器。

通过一些操作，ASEF滤波器可:变为:

$公式8：H^{*}=\frac{1}{N} \sum_{i} \frac{G_{i} \odot F_{i}^{*}}{F_{i} \odot F_{i}^{*}}$

只有当一张图像被用于训练时，MOSSE和ASEF都产生一个精准滤波器

当在少量的图像上训练时，ASEF滤波器是不稳定的。因为训练图像中一个频率包含少量能量(little energy，或者分母接近于0)时，公式8中的element-wise除法变得不稳定。平均大量的精准滤波器可以补偿这个问题，产生鲁棒的ASEF滤波器。因为MOSSE的分母是更多图像的能量和，所以很少产生很小的数，因此更加稳定。

正则化可以用来校正低能量频率和产生更稳定的ASEF滤波器。这个是通过给能量谱的每一个元素增加一个很小的值来实现的。 $F_i\odot F_i^*$ 被 $F_i \odot F_i^*+\epsilon$ 代替，其中 $\epsilon$ 是正则化参数。

正则化类似于来自OTF理论的结果，OTF理论通常与UMACE滤波器结合使用。结果表明，将背景噪声的能量谱加入到训练图像的能量谱中，可以产生较好的滤波效果，具有较好的抗噪性。这里作者加入了白噪声。下图显示了 $\epsilon$ 调整的效果。通过适当的正则化，所有的滤波器都能产生良好的峰值，并且应该足够稳定以产生良好的追踪结果。

Filter Initialization and Online Updates

公式8和5描述了滤波器如何在初始化阶段被构造。利用随机仿射变换构造训练集，在初始帧中产生的8个小扰动 $f_i$ 。训练输出也生成与他们的峰值相对应的目标中心。在追踪阶段，一个目标通常可以通过改变其旋转、比例、姿态、在不同光照条件下的移动，甚至通过经历非刚性形变来改变外观。因此滤波器需要快速调整以跟踪对象。平均值就是用来实现这个目的的。比如从第i帧学习到的SEF滤波器，可以计算为：

$公式9：H_{i}^{*}=\eta \frac{G_{i} \odot F_{i}^{*}}{F_{i} \odot F_{i}^{*}}+(1-\eta) H_{i-1}^{*}$

MOSSE滤波器可以表示为：

$\begin{aligned} 公式10：H_{i}^{*} &=\frac{A_{i}}{B_{i}} \\ 公式11：A_{i} &=\eta G_{i} \odot F_{i}^{*}+(1-\eta) A_{i-1} \\ 公式12：B_{i} &=\eta F_{i} \odot F_{i}^{*}+(1-\eta) B_{i-1} \end{aligned}$

其中 $\eta$ 是学习率，这放入了更多的权重在最近的帧中，使得先前帧的效果随着时间呈指数衰减。实际上，本文已经发现 $\eta=0.125$ 允许滤波器快速适应外观变化，同时仍然保持一个鲁棒的滤波器。

Failure Detection and PSR

如之前提到的一个简单的峰值强度测量被称为Peak to Sidelobe Ratio（PSR）。为了计算PSR，将相关输出g分为峰值和sidelobe，其中峰值是最大值，sidelobe是峰值周围除11 × 11窗口外的其余像素。PSR被定义为 $\frac {g_{max}-\mu_{sl}}{\sigma_{sl}}$ ，其中 $g_{max}$ 是峰值， $\mu_{sl}$ 和 $\sigma_{sl}$ 是sidelobe的均值和标准差。

在本文的实验中，在正常跟踪的情况下，对于UMACE，ASEF和MOSSE的PSR通常在20到60之间，这表明峰值非常强。作者已经发现，PSR下降到7.0左右时，表明物体被遮挡或跟踪失败。对于之前Navie的滤波器实现方式，PSR通常在3.0到10.0之间，对预测追踪的质量没有帮助。

Evaluation

最初，一个基于MOSSE的实时跟踪系统创建和评估在一个通过网络摄像头获取的实时视频上。实时反馈使得测试跟踪器配置的微小变化，以及对不同目标和跟踪条件下的跟踪器性能进行定性分析变得容易。这些测试为跟踪器的运行提供了有价值的简介，并有助于产生快速和健壮的跟踪器，这是本文提出的。

在http://www.cs.toronto.edu/∼dross/ivt/中，可以下载7个通用的测试视频，用于验证本文的方法。这些测试视频全部采用灰度，包括光线，姿势和外观上富有挑战性的变化。

Filter Camparison

在这个小节中，验证UMACE，ASEF，MOSSE滤波器的质量。他们被用于与基于具有在线更新的平均预处理跟踪窗口的naive的滤波器比较。跟踪输出被手动标记为良好的跟踪，跟踪偏离中心以及跟踪丢失。如下图所示：

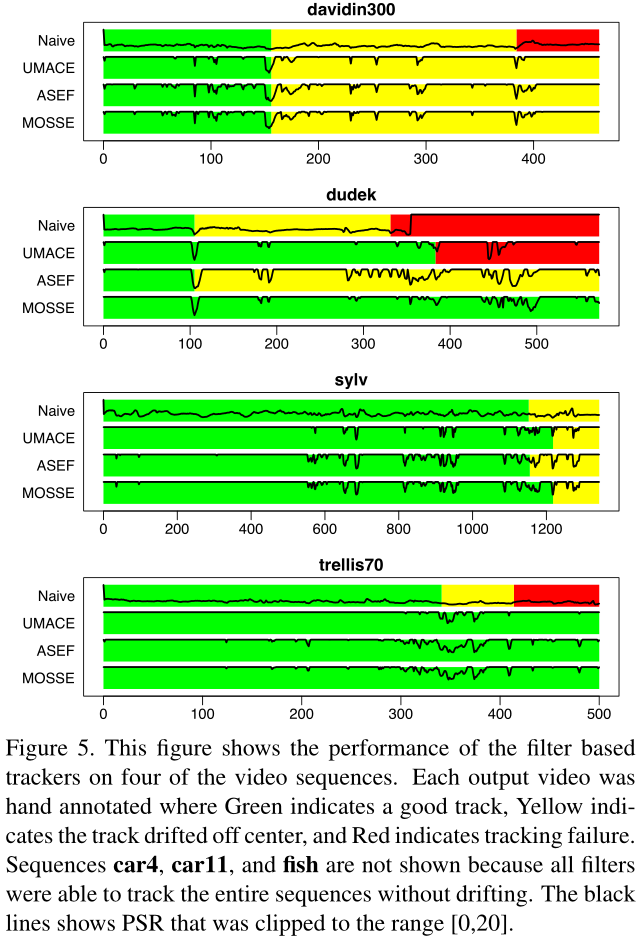
这张图展示了基于滤波器的跟踪器在四个视频中的表现。每一个输出视频中，用绿色表示好的追踪，黄色表示追踪偏离中心，红色表示跟踪失败。黑色的线显示clipped到[0,20]的PSR。

所有的滤波器都能够在测试集中发现比例变化，旋转变化，光照变化并且偏移很小的物体。大多数的偏移(drift)和跟踪失败的发生，目标都经历了一个大的平面外旋转(out-of-plane rotation)。如图6所示，过滤器倾向于跟踪目标中心的一个点，当目标旋转时，该点向目标边界移动，并且跟踪器最终处于大部分跟踪窗口被背景覆盖的状态(第一张图变到第二张图)。过滤器适应了这种半背景窗口，当目标旋转会正面姿势时(第二张图到第三张图)，滤波器会移动到一个新的位置，当然也有可能失去目标并跟踪背景。