「论文阅读」Multi-level Feature Learning for Contrastive Multi-view Clustering

论文名称：Multi-Level Feature Learning for Contrastive Multi-View Clustering

作者：Jie Xu, Huayi Tang, Yazhou Ren, Liang Peng, Xiaofeng Zhu, Lifang He

时间：2022

期刊或会议：Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition

代码：https://github.com/SubmissionsIn/MFLVC

Origin Abstract

Multi-view clustering can explore common semantics from multiple views and has attracted increasing attention. However, existing works punish multiple objectives in the same feature space, where they ignore the conflict between learning consistent common semantics and reconstructing inconsistent view-private information. In this paper, we propose a new framework of multi-level feature learning for contrastive multi-view clustering to address the aforementioned issue. Our method learns different levels of features from the raw features, including low-level features, highlevel features, and semantic labels/features in a fusion-free manner, so that it can effectively achieve the reconstruction objective and the consistency objectives in different feature spaces. Specifically, the reconstruction objective is conducted on the low-level features. Two consistency objectives based on contrastive learning are conducted on the highlevel features and the semantic labels, respectively. They make the high-level features effectively explore the common semantics and the semantic labels achieve the multi-view clustering. As a result, the proposed framework can reduce the adverse influence of view-private information. Extensive experiments on public datasets demonstrate that our method achieves state-of-the-art clustering effectiveness.

Abstract

多视图聚类(Multi-view clustering)能够从多个视图中探索公共的语义信息。现有的工作在同一个特征空间上惩罚(punish)多个目标，其中这些方法忽略了学习一致性的公共语义以及重建不一致的view-private信息之间的冲突。在这篇文章中，提出一个多级特征学习的新框架，用对比多视图聚类（contrastive multi-view clustering）来解决上述的问题。本文的方法通过一种不融合的方法从原始特征（raw feature）中学习不同级别的特征，包括低级特征，高级特征和语义标签/特征，以便于其可以有效地在不同的特征空间中重构目标(reconstruction objective)和一致性目标。具体来说，重构目标是在低级特征产生的。两个基于对比学习的一致性目标分别是在高级特征和语义标签产生的。这使得高级特征有效地探索出公共语义，并使语义标签实现了多视图聚类。结果，这个被提出的框架减少了view-private信息的不利影响。在公共数据集上的大量实验表明，该方法实现了最先进的聚类效果。

Introduction

由于多视图聚类(multi-view clustering, MVC)可以提供公共语义，使得多视图数据或多模态数据正受到越来越多的关注。

MVC的方法可以被粗略的分为：传统的方法和深度学习方法

传统的MVC方法是基于传统机器学习方法进行的聚类任务，可以分为以下三类

1. 子空间方法(subspace)
2. 矩阵分解方法(matrix factorization)
3. 图的方法(graph)

缺点：表示能力不足，较高的计算复杂度

深度学习的MVC方法因为出色的表示能力逐渐成为主流。之前那的深度学习MVC方法可以分为两类：

1. two-stage method

   其重点是从多个试图中分别学习显著性特征，并执行聚类任务

2. one-stage method

   其将特征学习与聚类任务嵌入到一个统一的框架中，以实现端到端的聚类

多视图数据包含两种信息：在所有视图中的通用语义、对每一个独立视图的view-private信息

举个例子：

一段文字和一张图片可以结合来描述公共语义，而文中的不相关上下文和图像中的背景像素对学习公共语义是没有价值的view-private信息。

在多视图学习，学习公共语义和避免无价值的view-private信息误导是一个始终相关的话题。尽管现有的方法已经实现了关键过程，但是他们仍然有一些缺点需要去解决

1. 许多MVC的方法尝试通过融合所有视图的特征来发现潜在的聚类模式(latent cluster patterns)。但与公共语义相比，无价值的view-private信息可能在融合过程中占据主导地位，从而干扰了聚类的质量。
2. 一些MVC的方法利用潜在特征的一致性目标来探索所有视图中的公共语义。但是，他们通常需要在相同的特征上重建目标，以避免繁琐的解决方案。这就导致了一种冲突：一致性目标试图尽可能地在所有视图中学习具有公共语义的特征，而重建目标则希望相同的特征去维护单独视图的view-private信息

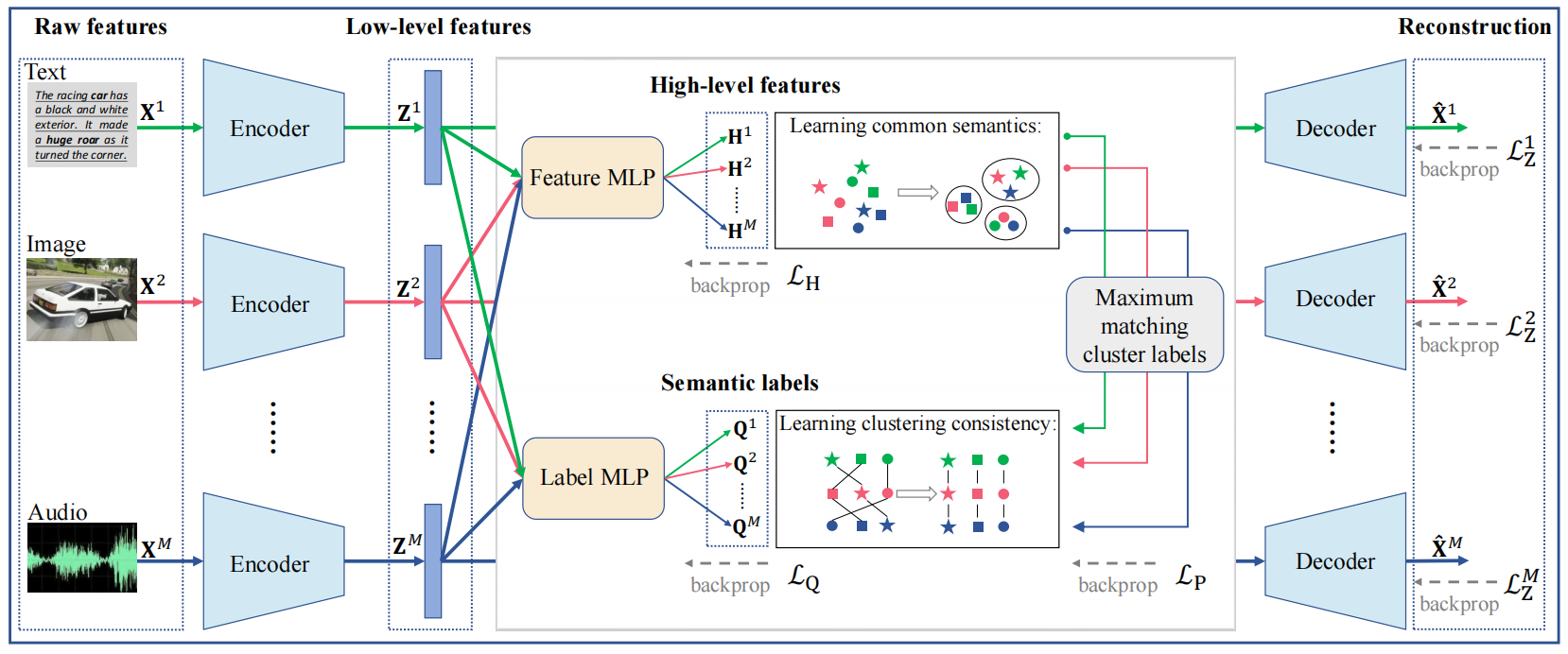
在这篇文章中提出了一个用于对比多视图聚类的新框架MFLVC，来解决之前提到的问题，结构如下图所示：

图1：

MFLVC的结构，在多级学习中，作者避免了直接特征融合，而是学习低级特征$Z^m$，高级特征$H^m$，以及每一个视图中的原始特征$X^m$得到的语义标签$Q^m$。重构目标$L_Z^m$是在$Z^m$上独立运行的。两个一致性目标($L_H$和$L_Q$)是分别在$\{H^m\}_{m=1}^M$和$\{Q^m\}_{m=1}^M$上运行的。此外，还对$L_p$进行了优化，利用了$\{H^m\}_{m=1}^M$的聚类信息来提高$\{Q^m\}_{m=1}^M$的聚类有效性。

目标：

1. 设计一个fusion-free的MVC模型，以避免所有的视图中view-primate信息的融合。
2. 为每个视图中的样本生成不同级别的特征，包括低级特征，高级特征和语义标签/特征。

首先利用一个自动编码器去从原始特征汇总学习低级特征，然后在低级特征上使用堆叠的两个MLP去得到高级特征和语义标签，每个MLP共享所有的视图，并有利于过滤view-private信息。此外，将语义标签作为anchors，其在高级特征中结合了语义标签，从而促进了聚类效果。

重构目标通过低级特征实现，两个一致性目标分别通过高级特征和语义标签实现。这两个一致性目标是由对比学习引导的，这使得高级特征更加关注挖掘所有视图中的一致性信息，也使得语义标签表一致性聚类并用于多视图聚类中。

贡献：

1. 设计了一个fusion-free的MVC方法去引导不同特征空间的不同目标去解决重建目标和一致性目标的冲突。这个方法有效地探索所有视同的公共语义，避免了无意义的view-private信息。
2. 可以用于同时实现高级特征和语义标签的一致性目标
3. 由于良好的框架设计，这个方法对超参数的设置也具有鲁棒性

Contrastive learning：

对比学习是一种注意力获取的无监督表示学习方法，思想是在一个特征空间中，最大化相似的正样本对，最小化负样本对。

Method

原始特征(raw feature)：多视图数据集$\left\{\mathbf{X}^{m} \in \mathbb{R}^{N \times D_{m}}\right\}_{m=1}^{M}$包括在M个视图上的N个样本，其中$\mathbf{x}_{i}^{m} \in \mathbb{R}^{D_{m}}$表示在第m个视图中的$D_m$维度样本。数据集被视为原始特征，其中多个视图有K个需要被发现的公共cluster模式。

Motivation

多视图通常有冗余和随机噪声，主流方法一直从原始特征中学习显著性表征。自编码器是一个广泛被使用的无监督模型，他可以将一个原始特征建模到可定制的特征空间中。具体来说，对第m个视图，$E^m(X^m;\theta^m)$和$D^m(Z^m;\phi^{m})$分别表示编码器和解码器。其中$\theta^m$和$\phi^m$是网络参数，$\mathbf{z}_{i}^{m}=E^{m}\left(\mathbf{x}_{i}^{m}\right) \in \mathbb{R}^{L}$是第i个样本的L维度的潜在特征，$L_Z^m$是输入$X^m$和输出$\hat{X}^m\in \mathbb{R}^{N \times D_{m}}$之间的重构损失。于是，所有视图的重构目标可以被表示为：

$$公式1：\mathcal{L}_{\mathbf{Z}}=\sum_{m=1}^{M} \mathcal{L}_{\mathbf{Z}}^{m}=\sum_{m=1}^{M} \sum_{i=1}^{N}\left\|\mathbf{x}_{i}^{m}-D^{m}\left(E^{m}\left(\mathbf{x}_{i}^{m}\right)\right)\right\|_{2}^{2}$$

基于$\{\mathbf{Z}^m=E^m(X^m)\}_{m=1}^M$，MVC的目的是挖掘所有视图中的公共语义，提高聚类质量。

现有的MVC方法仍然存在如下两个挑战：

1. 直接融合所有视图得到一个通用的表征，会使得这个表征的视图中包含一致性语义和view-private信息，后者是没有意义甚至会对模型进行误导，从而印象融合特征的质量，导致poor的聚类效果。
2. 通过在潜在性目标上引导一个一致性目标去学习一致的多视图特征，从而实现公用语义的探索，并最小化所有视图中的相关特征的距离。这使得一致性目标和重建目标都被推到相同的特征之中，而一致性目标的目的是学习公用特征，重建目标希望获得view-private信息，这两者冲突了。

Multi-view Contrastive Learning

因为从公式1得到的潜在特征$\{\mathbf{Z}^m\}_{m=1}^M$混合了公用语义和view-private信息，本文将$\{\mathbf{Z}^m\}^M_{m=1}$当做低级特征，学习另一个级别的特征，比如高级特征。本文在$\{\mathbf{Z}^m\}_{m=1}^M$上堆叠了一个MLP以得到高级特征$\{\mathbf{H}^m\}_{m=1}^M$，其中$\mathbf{h}_i^m\in \mathbb{R}^{H}$，特征MLP是一层线性的MLP，可以表示为$F\left(\left\{\mathbf{Z}^{m}\right\}_{m=1}^{M} ; \mathbf{W}_{H}\right)$。在低级特征空间中，利用重构目标公式1去保持$\{\mathbf{Z}^m\}^M_{m=1}$的表示能力，同时避免模型坍塌的问题。在高级特征空间中，通过对别学习得到一致性目标，使得$\{\mathbf{H}^m\}^M_{m=1}$关注学习所有视图中的公用语义。

具体来说，每一个高级特征$\mathbf{h}_i^m$有$(MN-1)$个特征对，例如$\left\{\mathbf{h}_{i}^{m}, \mathbf{h}_{j}^{n}\right\}_{j=1, \ldots, N}^{n=1, \ldots, M}$，其中$\left\{\mathbf{h}_{i}^{m}, \mathbf{h}_{i}^{n}\right\}_{n \neq m}$，是$(M-1)$个正特征对，并设置$M(N-1)$个特征对是负特征对。在对比学习中，正样本对的相似性应该被最大化，而负样本对的相似性应该被最小化。余弦距离可以被用于评估两个特征之间的相似性。

$$公式2：d\left(\mathbf{h}_{i}^{m}, \mathbf{h}_{j}^{n}\right)=\frac{\left\langle\mathbf{h}_{i}^{m}, \mathbf{h}_{j}^{n}\right\rangle}{\left\|\mathbf{h}_{i}^{m}\right\|\left\|\mathbf{h}_{j}^{n}\right\|},$$

其中$\langle\cdot, \cdot\rangle$是点积运算。然后，$\mathbf{H}^m$和$\mathbf{H}^n$的特征对比损失可以用如下公式表示：

$$公式3：\ell_{f c}^{(m n)}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{d\left(\mathbf{h}_{i}^{m}, \mathbf{h}_{i}^{n}\right) / \tau_{F}}}{\sum_{j=1}^{N} \sum_{v=m, n} e^{d\left(\mathbf{h}_{i}^{m}, \mathbf{h}_{j}^{v}\right) / \tau_{F}}-e^{1 / \tau_{F}}}$$

其中$\tau_F$表示temperature parameter（活性系数）。在本文中，所有视图的多视图特征对比损失计算方式为：

$$公式4：\mathcal{L}_{\mathbf{H}}=\frac{1}{2} \sum_{m=1}^{M} \sum_{n \neq m} \ell_{f c}^{(m n)}$$

每一个视图的特征可以写做$\mathbf{H}^{m}=\mathbf{W}_{H} \mathbf{Z}^{m}=\mathbf{W}_{H} E^{m}\left(\mathbf{X}^{m}\right)$。编码器$E^m$是用于过滤$\mathbf{X}^m$的随机噪声的。在$\mathbf{Z}^m$重构目标避免了模型坍塌，也将通用语义和view-private信息保存在$\mathbf{Z}^m$中，$\mathbf{W}_H$用于过滤$\{\mathbf{Z}^m\}^M_{m=1}$中的view-private信息。在$\{\mathbf{H}^m\}^M_{m=1}$中的一致性对象，允许他们挖掘所有视图中的通用信息。结果

Learning semantic labels

具体来说，本文通过在低级特征(比如，$L\left(\left\{\mathbf{Z}^{m}\right\}_{m=1}^{M} ; \mathbf{W}_{Q}\right)$)上使用一个共享标签的MLP，得到所有视图的cluster assignments($\left\{\mathbf{Q}^{m} \in \mathbb{R}^{N \times K}\right\}_{m=1}^{M}$). MLP的最后一层使用softmax操作输出可能性，$q_{ij}^m$表示在第m个视图的第i个样本属于第j个聚类的可能性。因此，语义标签通过聚类分配(cluster assignments)的最大元素进行区分。

所有视图的相同聚类标签表示相同的语义聚类。换句话说语义标签$\left\{\mathbf{Q}_{\cdot j}^{m}\right\}_{m=1}^{M}\left(\mathbf{Q}_{\cdot j}^{m} \in \mathbb{R}^{N}\right)$需要被一致化。与学习高级特征相似，本文采用对比学习的方式获得一致性目标。对于第m个视图，相同的聚类标签$\mathbf{Q}_j^m$有$(MK-1)$个标签对$\left\{\mathbf{Q}_{\cdot j}^{m}, \mathbf{Q}_{\cdot k}^{n}\right\}_{k=1, \ldots, K}^{n=1, \ldots, M}$，其中$\left\{\mathbf{Q}_{i}^{m}, \mathbf{Q}_{i}^{n}\right\}_{n \neq m}$被构造为$(M-1)$个正标签对，$M(K-1)$个负标签对。将$\mathbf{Q}^m$和$\mathbf{Q}^n$之前的标签对比函数定义为：

$$公式5：\ell_{l c}^{(m n)}=-\frac{1}{K} \sum_{j=1}^{K} \log \frac{e^{d\left(\mathbf{Q}_{\cdot j}^{m}, \mathbf{Q}_{\cdot j}^{n}\right) / \tau_{L}}}{\sum_{k=1}^{K} \sum_{v=m, n} e^{d\left(\mathbf{Q}_{\cdot j}^{m}, \mathbf{Q}_{\cdot k}^{v}\right) / \tau_{L}}-e^{1 / \tau_{L}}}$$

其中$\tau_L$是temperature parameter。因此，面向聚类的一致性目标可以定义为：

$$公式6：\mathcal{L}_{\mathbf{Q}}=\frac{1}{2} \sum_{m=1}^{M} \sum_{n \neq m} \ell_{l c}^{(m n)}+\sum_{m=1}^{M} \sum_{j=1}^{K} s_{j}^{m} \log s_{j}^{m}$$

其中$s_j^m = \frac 1N\sum_{i=1}^Nq_{ij}^m$，公式6的第一部分目的是学习所有视图的聚类一致性。第二部分是正则项，这通常被用于避免所有的样本都设置到一个单独的cluster中。

总的来说，多视图对比学习损失函数可以由3个部分组成：

$$公式7：\begin{aligned} \mathcal{L} &=\mathcal{L}_{\mathbf{Z}}+\mathcal{L}_{\mathbf{H}}+\mathcal{L}_{\mathbf{Q}} \\ &=\mathcal{L}_{\mathbf{Z}}\left(\left\{\mathbf{X}^{m}, \hat{\mathbf{X}}^{m}\right\}_{m=1}^{M} ;\left\{\theta^{m}, \phi^{m}\right\}_{m=1}^{M}\right) \\ &+\mathcal{L}_{\mathbf{H}}\left(\left\{\mathbf{H}^{m}\right\}_{m=1}^{M} ; \mathbf{W}_{H},\left\{\theta^{m}\right\}_{m=1}^{M}\right) \\ &+\mathcal{L}_{\mathbf{Q}}\left(\left\{\mathbf{Q}^{m}\right\}_{m=1}^{M} ; \mathbf{W}_{Q},\left\{\theta^{m}\right\}_{m=1}^{M}\right) \end{aligned}$$

其中$\mathcal{L}_{\mathbf{Z}}$是在低级特征$\{\mathbf{Z}^m\}^M_{m=1}$上执行的重构目标，以避免模型坍塌。一致性目标$\mathcal{L}_{\mathbf{H}}$和$\mathcal{L}_{\mathbf{Q}}$被分别设计去用于学习高级特征和聚类分配(cluster assignments)。从$\{\mathbf{Z}^m\}^M_{m=1}$中学习$\{\mathbf{H}^m\}^M_{m=1}$而不是从$\{\mathbf{H}^m\}^M_{m=1}$中，这可以避免$\mathbf{W}_h$和$\mathbf{W}_Q$的影响。然而$\mathbf{W}_H$和$\mathbf{W}_Q$将不会被$\mathcal{L}_{\mathbf{Z}}$的梯度影响。

Semantic Clustering with High-level Features

通过多视图对比学习，模型同时学习高级特征$\{\mathbf{H}^m\}^M_{m=1}$和一致性聚类分布$\{\mathbf{Q}^m\}^M_{m=1}$。将$\{\mathbf{Q}^m\}^M_{m=1}$当做anchors，将他们与$\{\mathbf{H}^m\}^M_{m=1}$之间的clusters进行匹配。通过这种方式，利用包括高级特征的聚类信息去粗剪语义标签的聚类效果。

本文采用K-means去获得每一个视图上的聚类信息。对于第m个视图，让$\left\{\mathbf{c}_{k}^{m}\right\}_{k=1}^{K} \in \mathbb{R}^{H}$表示第K个聚类中心，于是有：

$$公式8：\min _{\mathbf{c}_{1}^{m}, \mathbf{c}_{2}^{m}, \ldots, \mathbf{c}_{K}^{m}} \sum_{i=1}^{N} \sum_{j=1}^{K}\left\|\mathbf{h}_{i}^{m}-\mathbf{c}_{j}^{m}\right\|_{2}^{2}$$

所有样本$\mathbf{p}^{m} \in \mathbb{R}^{N}$的聚类标签可以通过下面的公式得到

$$公式9：p_{i}^{m}=\operatorname{argmin}\left\|\mathbf{h}_{i}^{m}-\mathbf{c}_{j}^{m}\right\|_{2}^{2} .$$

令$\mathbf{I}^m\in\mathbb{R}^N$表示使用标签MLP的聚类标签输出，其中$l_i^m=argmax_jq_{ij}^m$。之二的注意的是，由$\mathbf{p}^m$和$\mathbf{I}^m$表示的clusters彼此并不对应。因为，聚类一致性通过公式6获取。$l_i^m$和$l_i^n$表示相同的cluster。因此，可以把$\mathbf{I}^m$当做anchors去修改$\mathbf{p}^m$通过下面的最大匹配公式

$$公式10：\\ \begin{aligned} & \min _{\mathbf{A}^{m}} \mathbf{M}^{m} \mathbf{A}^{m} \\ \text { s.t. } & \sum_{i=1} a_{i j}^{m}=1, \sum_{j=1} a_{i j}^{m}=1, \\ & a_{i j}^{m} \in\{0,1\}, i, j=1,2, \ldots, K, \end{aligned}$$

其中$\mathbf{A}^m\in\{0,1\}^{K\times K}$是布尔矩阵$\mathbf{M}^m\in\mathbb{R}^{K\times K}$是开销矩阵(cost matrix)。$\mathbf{M}^m=max_{i,j}\tilde{m}_{i j}^{m}-\tilde{\mathbf{M}}^{m}$，$\tilde{m}_{i j}^{m}=\sum_{n=1}^{N} \mathbb{1}\left[l_{n}^{m}=i\right] \mathbb{1}\left[p_{n}^{m}=j\right]$，其中$\mathbb{l}[\cdot]$表示指标函数。第i个样本的聚类分布$\hat{\mathbf{p}}\in \{0,1\}^K$被定义为一个one-hot向量。当k满足$k=k \mathbb{1}\left[a_{k s}^{m}=1\right] \mathbb{1}\left[p_{i}^{m}=s\right], k, s \in\{1,2, \ldots, K\}$时,$\hat{\mathbf{p}}_i^m$的第k个元素是l。然后，通过交叉熵对模型进行微调：

$$公式11：\mathcal{L}_{\mathbf{P}}=-\sum_{m=1}^{M} \hat{\mathbf{P}}^{m} \log \mathbf{Q}^{m}$$

其中$\hat{\mathbf{P}}^{m}=\left[\hat{\mathbf{p}}_{1}^{m} ; \hat{\mathbf{p}}_{2}^{m} ; \ldots ; \hat{\mathbf{p}}_{N}^{m}\right] \in \mathbb{R}^{N \times K}$，通过这种方式，可以转换成学习语义只是去促进聚类。最后，第i个样本的语义标签为：

$$公式12：y_{i}=\underset{j}{\operatorname{argmax}}\left(\frac{1}{M} \sum_{m=1}^{M} q_{i j}^{m}\right)$$

优化：MFLVC的优化过程，可以用算法1表示。具体来说本文采用小批量梯度下降算法来训练模型。他由多个自动编码器，一个特征MLP和标签MLP组成。自编码器的初始化方式为公式1. 多视图对比学习通过公式7得到公用语义和聚类一致性。在多视图对比学习之后，从高级特征得到的聚类标签通过最大化匹配公式10所修改。修改后的聚类标签通过公式11被用于调整模型。高级特征提取器包括编码器和特征MLP，而标签预测器包括编码器和标签MLP。

算法1：MFLVC的优化

输入：多尺度数据集$\{\mathbf{X}^m\}^M_{m=1}$；聚类数量K；活性参数$\tau_F$和$\tau_L$

1. 通过最小化公式1初始化$\left\{\theta^{m}, \phi^{m}\right\}_{m=1}^{M}$
2. 通过公式7优化$\mathbf{W}_H$，$\mathbf{W}_Q$，$\left\{\theta^{m}, \phi^{m}\right\}_{m=1}^{M}$
3. 通过公式8和9，计算聚类标签
4. 通过解决公式10，匹配多视图聚类标签
5. 通过公式11，调整$\mathbf{W}_Q$，$\{\theta\}_{m=1}^M$
6. 通过公式12，计算语义标签。

输出：标签预测器$\left\{\left\{\theta^{m}\right\}_{m=1}^{M}, \mathbf{W}_{Q}\right\}$

高级特征提取器$\left\{\left\{\theta^{m}\right\}_{m=1}^{M}, \mathbf{W}_{H}\right\}$

Experiments

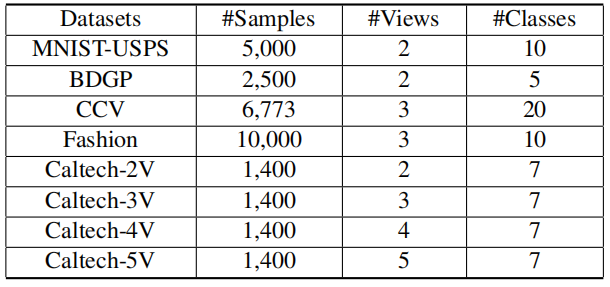
使用的数据集，样本数，视图数，类别数：

验证指标：ACC,NMI,PUR

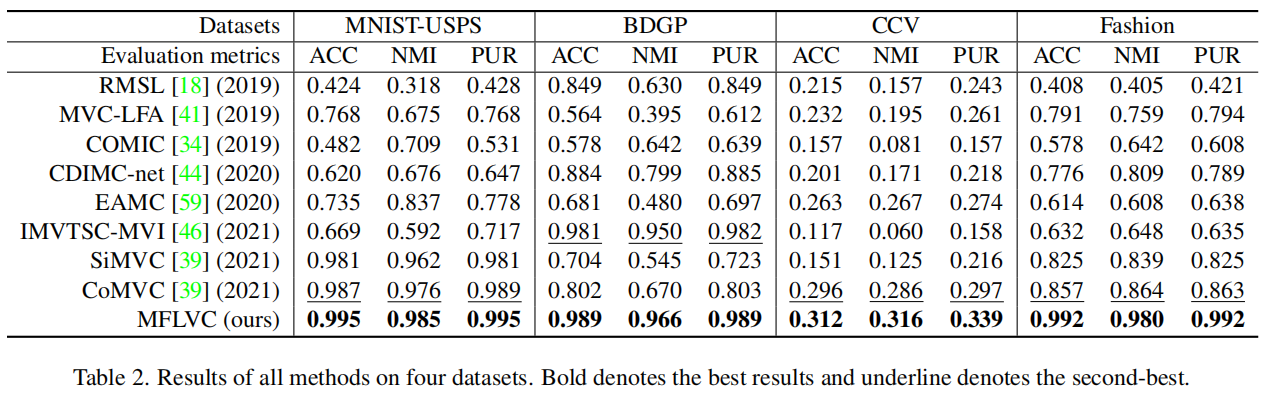
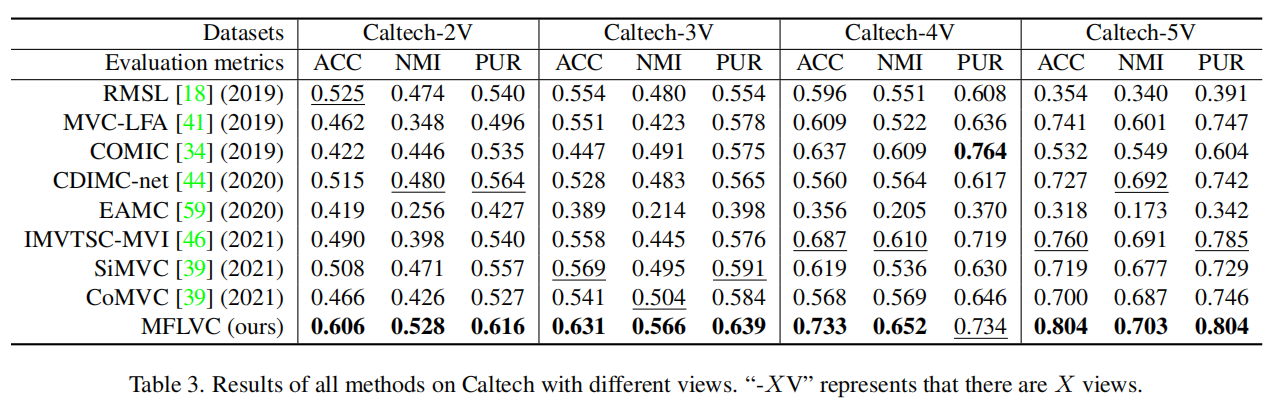
结果：

此外Caltech上通过改变不同数据集的视图数验证MFLVC在视图数变化情况的有效性

Model Analysis

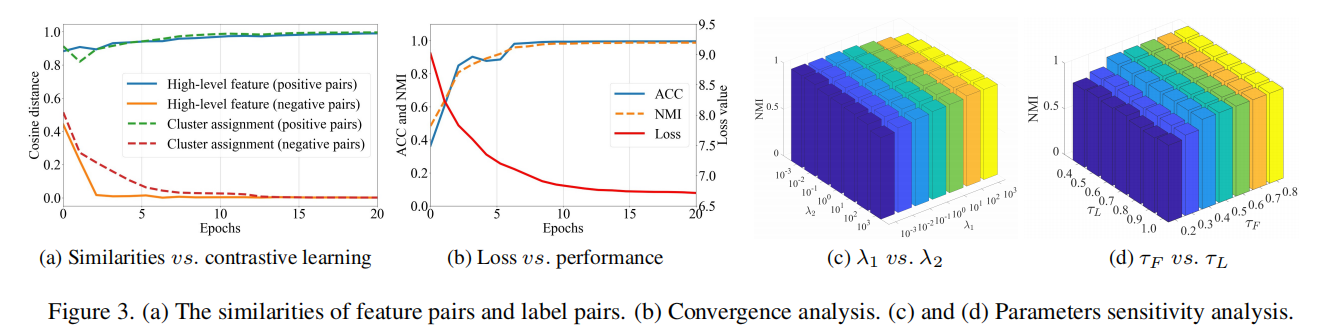
图中高级特征和低级特征的聚类都逐渐变得清晰。低级特征是不密集的，因为低级特征通过重建保持了样本的多样性。高级特征是密集的，有更好的低纬度manifolds。

收敛性分析：图中b图在loss下降时指标提高，说明具有比较好的收敛性

参数敏感度分析：从c图和d图中可知对这两个超参数都不敏感。

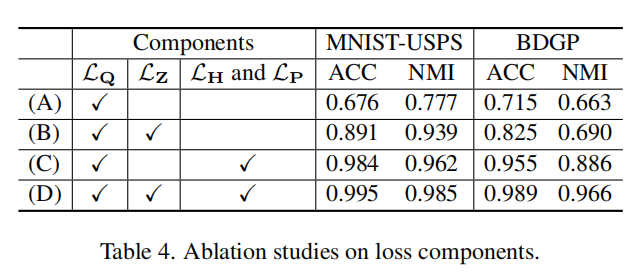
Ablation Studies

loss部分:

loss的部分你主要包括公式7和公式11的损失，消融实验的具体数值如下图：

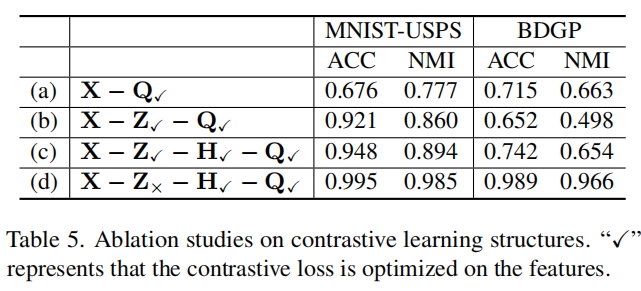
对比学习结构部分：

a表示从原始特征X中对比学习语义标签Q

b表示先从原始特征X中对比学习低级特征Z，再从低级特征对比学习语义标签Q

c表示基于低级特征Z，堆叠一个特征MLP去得到高级特征H，然后在Z,H,Q上使用对比学习

d表示只在H,Q上做对比学习，而Z在重建目标上保留