「论文阅读」Deep Incomplete Multi-view Clustering via Mining Cluster Complementarity

论文名称：Deep Incomplete Multi-view Clustering via Mining Cluster Complementarity

作者：Jie Xu, Huayi Tang, Yazhou Ren, Liang Peng, Xiaofeng Zhu, Lifang He

时间：2022

期刊或会议：AAAI2022

代码：https://github.com/SubmissionsIn/DIMVC

Origin Abstract

Incomplete multi-view clustering (IMVC) is an important unsupervised approach to group the multi-view data containing missing data in some views. Previous IMVC methods suffer from the following issues: (1) the inaccurate imputation or padding for missing data negatively affects the clustering performance, (2) the quality of features after fusion might be interfered by the low-quality views, especially the inaccurate imputed views. To avoid the above issues, this work presents an imputation-free and fusion-free deep IMVC framework. First, the proposed method builds a deep embedding feature learning and clustering model for each view individually. Our method then nonlinearly maps the embedding features of complete data into a high-dimensional space to discover linear separability. Concretely, this paper provides an imple mentation of the high-dimensional mapping as well as shows the mechanism to mine the multi-view cluster complemen tarity. This complementary information is then transformed to the supervised information with high confifidence, aiming to achieve the multi-view clustering consistency for the com plete data and incomplete data. Furthermore, we design an EM-like optimization strategy to alternately promote feature learning and clustering. Extensive experiments on real-world multi-view datasets demonstrate that our method achieves superior clustering performance over state-of-the-art methods.

Abstract

不完整的多视图聚类(IMVC)是一个重要的无监督方法，去分组在某些视图上含有缺失信息的多视图数据数据。

之前的IMVC方法存在如下问题：

1. 不准确的归类或填充确实数据对聚类效果有负面影响
2. 融合后的特征质量可能受到低质量视图的影响

为了避免这两个问题，本文提出了一个不用归类，不用融合的深度IMVC框架。首先，提出的方法在每一个视图上单独构造了一个深度嵌入特征学习和聚类的模型。本文的方法非线性映射完整数据的嵌入特征到更高的维度空间，去发掘线性可分离性。具体来说，本文提供了高维映射的互补性，也展示了这个机制去挖掘多视图聚类的互补性。

这个互补信息被转化成高置信度的监督信息，目的是为完整数据和不完整的数据取得多视图聚类的一致性。

Introduction

在实际应用中，数据通常有从不同来源收集的多个视图，比如：分类，社区检测(community detection)，降维，跨模态检索。多视图聚类的目的是通过挖掘隐藏在多视图数据中的互补性来提高模型的有效性。现在已经有很多多视图聚类的方法，这些方法通常用完整的多视图数据处理，即所有视图的信息都是可以观察的数据。

图像和文本是描述一个场景的两个视图，但是只有一些图像有文本描述。不完整的多视图数据会不可避免得使得现有的多视图聚类方法首先和难以应用。于是就有了对部分多视图聚类和不完整多视图聚类(IMVC)问题的研究。

IMVC方法可以分为传统方法和深度学习方法两类。传统的方法通常使用0或者均值来填充缺失的数据，还有设计特殊的机制学习技术去实现多视图聚类，比如非负矩阵分解法，子空间学习法，核方法，图方法。然而传统的IMVC方法仍然受限于他们的表达能力和高复杂性。

最近深度学习的IMVC方法因为其有力的生成能力和可伸缩性逐渐收到关注。深度学习的IMVC方法，通常使用归类策略(imputation stategies)在多视图聚类之前去为缺失的数据推理可能的值。比如：

1. 使用GAN的优势去生成确实数据中的期望数据
2. 使用对比学习的方法恢复缺失的数据

但这些方法，仍然存在以下问题：

1. 归类策略的有效性依赖于归类数据的质量。基于完整数据去正确地估计缺失数据是困难的，尤其是缺失数据特别大的时候。
2. 因为缺失数据的GT是不知道的，所以衡量归类的质量也是困难的。
3. 现有的IMVC方法通常通过融合过程去探索多视图数据当中的互补信息。比如
   1. 通过融合多个相似性矩阵来挖掘互补信息。
   2. 利用融合层去挖掘互补信息
4. 但一些视图可能会继承低质量或者不正确的归类，他们会对融合过程产生负面影响

在这篇文章中提出了一个不用归类，不用融合的深度IMVC框架(DIMVC)去解决上述问题。这个框架使得确实的数据不需要被归类或者填充，以及聚类分布不需要依赖多视图的融合过程。这个框架要解决两个挑战

1. 要发展新的策略在不融合模型中探索互补信息
2. 在没有归类的前提下，获得完整数据和不完整数据的一致性聚类分布是困难的

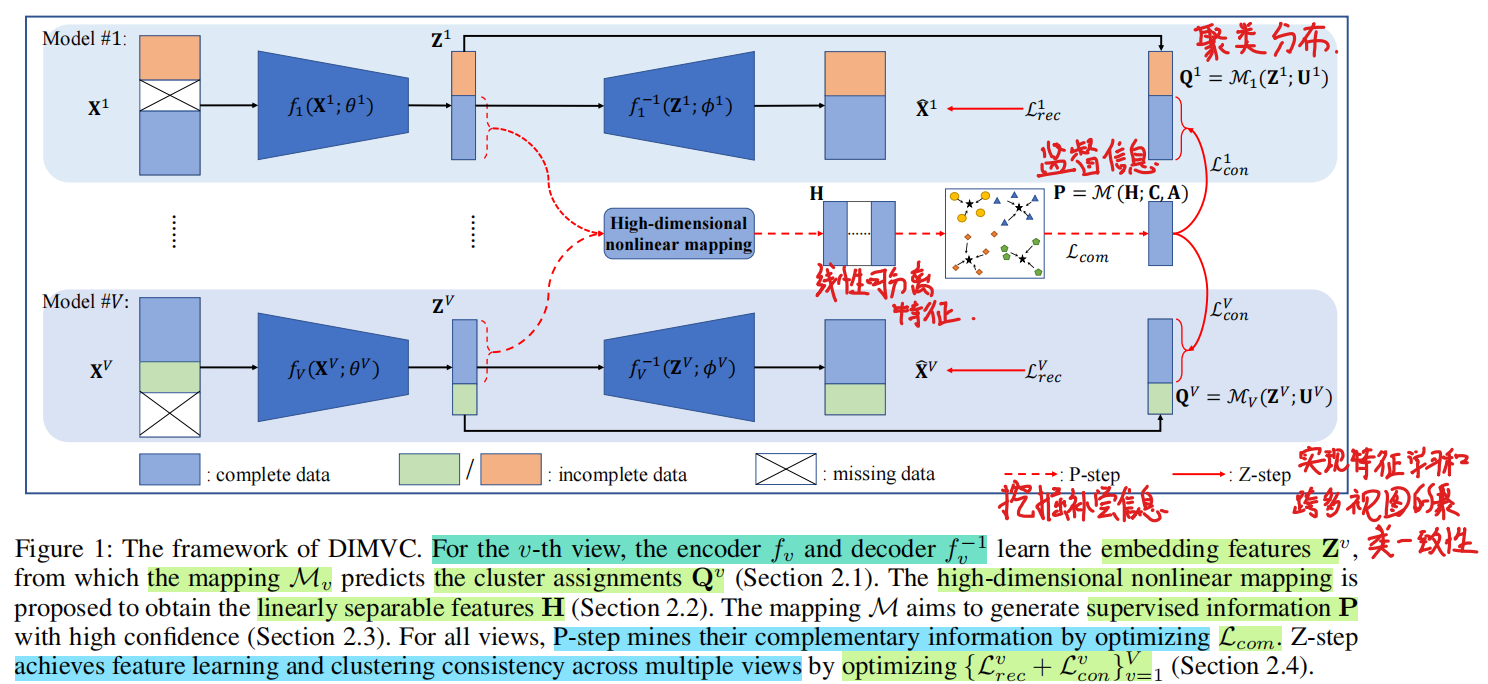
本文提出的DIMVC框架如下图：

具体来说，首先每个视图上所有可观察的数据中构建一个独立的模型，每个模型由一个自编码器和一个聚类映射构成。基于作者的观察，多视图的互补信息可以通过非线性映射描述。于是作者通过一个高维映射解决了第一个挑战。具体来说完整数据的嵌入特征被非线性映射到一个级联的权重特征空间中，其中，高度可分离的视图被设置了很高的权重。线性可分离聚类信息被和钻花为高维度特征，叫做多视图聚类互补性(multi-view cluster complementarity)。这个互补的聚类信息被转化为高置信度的监督信息，目的是获取所有视同中的一致性聚类分布，从而解决第二个挑战。此外，还提出了类EM的优化策略，包括P-step和Z-step，去交替促进特征学习和和聚类。

本文的主要贡献如下：

1. 提出了一个新颖的深度IMVC方法，是一个不用归类也不用融合的框架，他可以避免不准确归类早造成的噪声，减轻低质量数图的干扰。
2. 提出通过多视图中的一个非线性映射挖掘高维特征空间中的补偿信息。
3. 设计了一个交替优化策略，有效地优化了DIMVC框架。

Method

N个样本的不完整的多视图数据集$\left\{\mathbf{X}^{v} \in \mathbb{R}^{N_{v} \times D_{v}}\right\}_{v=1}^{V}$，$V$是视图的数量，对于第v个视图，$D_v$是数据的维度，$N_v$表示样本的数量其中由于数据缺失，总样本数通常会比视图样本数大。K是要被聚类的类别数。使用$\mathcal{X}$。

Deep model of feature learning and clustering

首先，在每个模态中引入了特征学习和聚类模型。深度自编码器能够捕获数据中的显著特征并被运用在许多无监督领域中。所以本文使用自编码器，将衣钩的多视图数据转化为clustering-friendly的嵌入特征。在第v个视图中，通过编码器和解码器学习的嵌入特征表示为$\mathbf{Z}^v$。

编码器：$f_{v}\left(\mathbf{X}^{v} ; \theta^{v}\right):\mathbf{X}^{v} \in \mathbb{R}^{N_{v} \times D_{v}} \longmapsto \mathbf{Z}^{v} \in \mathbb{R}^{N_{v} \times d_{v}}$

解码器：$f_{v}^{-1}\left(\mathbf{Z}^{v} ; \phi^{v}\right): \mathbf{Z}^{v} \in \mathbb{R}^{N_{v} \times d_{v}} \longmapsto \hat{\mathbf{X}}^{v} \in \mathbb{R}^{N_{v} \times D_{v}}$

其中$d_v$是嵌入特征的维度，$\theta^v$和$\phi^v$是自编码器网络的可学习参数。$\mathbf{X}^v$和$\hat{\mathbf{X}}^v$之间的重构损失可以表示为：

$$公式1： \begin{aligned} \mathcal{L}_{r e c} &=\sum_{v=1}^{V}\left\|\mathbf{X}^{v}-f_{v}^{-1}\left(\mathbf{Z}^{v}\right)\right\|_{F}^{2} \\ &=\sum_{v=1}^{V} \sum_{i=1}^{N_{v}}\left\|\mathbf{x}_{i}^{v}-f_{v}^{-1}\left(f_{v}\left(\mathbf{x}_{i}^{v}\right)\right)\right\|_{2}^{2} \end{aligned}$$

利用一个参数映射，$\mathcal{M}_{v}\left(\mathbf{Z}^{v} ; \mathbf{U}^{v}\right): \mathbf{Z}^{v} \in \mathbb{R}^{N_{v} \times d_{v}} \longmapsto \mathbf{Q}^{v} \in \mathbb{R}^{N_{v} \times K}$，去获取软聚类映射$\mathbf{Q}^v$。其中$\mathbf{U}^{v}=\left[\mathbf{u}_{1}^{v} ; \mathbf{u}_{2}^{v} ; \ldots ; \mathbf{u}_{K}^{v}\right] \in \mathbb{R}^{K \times d_{v}}$表示可学习的参数。具体来说

$$公示2：q_{i j}^{v}=\frac{\left(1+\left\|\mathbf{z}_{i}^{v}-\mathbf{u}_{j}^{v}\right\|_{2}^{2}\right)^{-1}}{\sum_{j=1}^{K}\left(1+\left\|\mathbf{z}_{i}^{v}-\mathbf{u}_{j}^{v}\right\|_{2}^{2}\right)^{-1}} \in \mathbf{Q}^{v}$$

在第v个视图中$\mathbf{u}_j^v$是第j个聚类中心，$q_{ij}^v$表示嵌入特征分配在第j个聚类的可能性。

Multi-view cluster complementarity

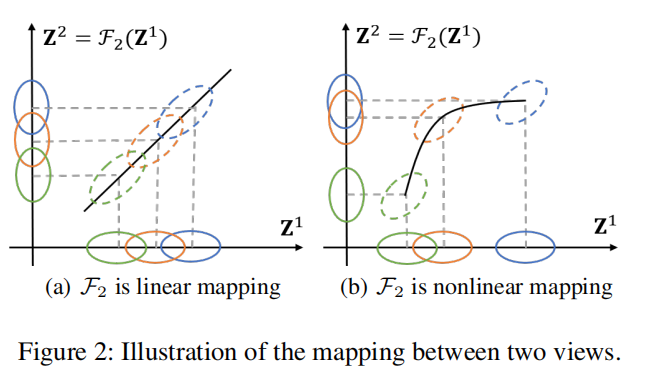
因为多视图共享相同的语义信息，对于每一个视图可以被认为是其他视图的映射，如下图：

图中(a)，如果一个视图是其他视图的线性映射，他们是没有互补信息的。但是如果在多视图中存在互补关系，在一个视图的不可分离性聚类在其他视图是可分离的，互补性可以通过如图中b的非线性映射描述。

通过考虑聚类分布作为样本的伪标签的方式，可以将聚类问题看做分类问题。

假设1：

一个负载的分类问题可以被看做是线性可分的，当其非线性映射到高维度空间时。

根据假设1，本文提出通过线性映射$\mathcal{H}$映射多视图嵌入到高维空间中。在本文中，这个映射嵌入特征进一个级联的权重特征空间(CWFS)

$$公式3：\mathbf{H}=\mathcal{H}\left(\left\{\mathbf{Z}^{v}\right\}_{v=1}^{V}\right)=\left(w_{1} \mathbf{Z}^{1}, w_{2} \mathbf{Z}^{2}, \ldots, w_{V} \mathbf{Z}^{V}\right)$$

其中$\mathbf{H} \in \mathbb{R}^{|\mathcal{X}| \times \sum_{v=1}^{V} d_{v}}$表示得到的高级特征，$w_v$是权重，其计算方式为：

$$公式4：w_{v}=1+\log \left(1+\frac{\sigma\left(\mathbf{U}^{v}\right)}{\sum_{v} \sigma\left(\mathbf{U}^{v}\right)}\right)$$

其中$\sigma(\mathbf{U}^v)$是第v个视图的聚类中心$\mathbf{U^v}$的方差。CWFS的权重$\{w_v\}^V_{v=1}$被提出，用于促进高度可分离视图影响，也用于减少其他含有不清晰聚类结构视图的影响。通过这种方式，映射$\mathcal{H}$可以使得CWFS中样本的聚类分布与高度可分性视图中的聚类分配一致。

理论1：

$\mathbf{H}$是$\{\mathbf{Z}^v\}_{v=1}^V$一个高维的非线性映射，高维特征$\mathbf{H}$对比于任何一个视图中v的$Z^v$是更加线性可分的。

证明：

考虑到每个视图的每个样本的嵌入特征$\mathbf{z}_{i}^{v}$，假设有位置的映射使得$\mathbf{z}_{i}^{t}=\mathcal{F}_{t}\left(\mathbf{z}_{i}^{v}\right) \in \mathbb{R}^{d_{t}}$并且$t \in \{1,2, \ldots V\}$。如果一些映射$\left\{\mathcal{F}_{t}: \mathbf{Z}^{v} \longmapsto \mathbf{Z}^{t}\right\}_{t \neq v}^{V}$是非线性的，所有嵌入特征的连接$\left(\mathbf{z}_{i}^{1}, \mathbf{z}_{i}^{2}, \ldots, \mathbf{z}_{i}^{V}\right)=\left(\mathcal{F}_{1}\left(\mathbf{z}_{i}^{v}\right), \mathcal{F}_{2}\left(\mathbf{z}_{i}^{v}\right), \ldots, \mathcal{F}_{V}\left(\mathbf{z}_{i}^{v}\right)\right) \in \mathbb{R}^{\sum_{v=1}^{V} d_{v}}, \sum_{v=1}^{V} d_{v}>d_{v}$是$\mathbf{z}_{i}^{v}$的一个高纬度非线性映射。此外$w_{v}$是一个非线性权重函数，提出的$\mathcal{H}:\left\{\mathbf{Z}^{v}\right\}_{v=1}^{V} \longmapsto \mathbf{H}$也是一个用于所有视图的嵌入特征的高维非线性映射。因此，假设1和理论1得证。

基于理论1，映射$\mathcal{H}$确保得到$\mathbf{H}$比单一视图的嵌入特征包含更多可分离的聚类模式。这在论文中就叫做多视图聚类补偿性。在CWFS中，可以通过下面的式子得到新的聚类中心$\mathcal{C}$：

$$公式5：\begin{aligned} \mathcal{L}_{c o m} &=\min _{\left\{\mathbf{C}^{v}\right\}_{v=1}^{V}} \sum_{i \in \mathcal{X}} \sum_{j=1}^{K} \sum_{v=1}^{V}\left\|w_{v} \mathbf{z}_{i}^{v}-\mathbf{c}_{j}^{v}\right\|_{2}^{2} \\ &=\min _{\mathbf{C}} \sum_{i \in \mathcal{X}} \sum_{j=1}^{K}\left\|\mathbf{h}_{i}-\mathbf{c}_{j}\right\|_{2}^{2} \end{aligned}$$

其中：$\mathbf{C} \in \mathbb{R}^{K \times \sum_{v=1}^{V} d_{v}}$，$\mathbf{c}_{j}=\left(\mathbf{c}_{j}^{1}, \mathbf{c}_{j}^{2}, \ldots, \mathbf{c}_{j}^{V}\right) \in \mathbb{R}^{\sum_{v=1}^{V} d_{v}}$。多视图聚类的中心行是从完整数据$\mathcal{X}$中学习的

Multi-view clustering consistency

在CWFS中，所有视图中的线性可分离聚类信息被转化为高维特征$\mathbf{H}$。本文能通过$\mathcal{M}(\mathbf{H} ; \mathbf{C}, \mathbf{A}): \mathbf{H} \in\mathbb{R}^{|\mathcal{X}| \times \sum_{v=1}^{V} d_{v}} \longmapsto \mathbf{P} \in \mathbb{R}^{|\mathcal{X}| \times K}$生成监督信息，其过程可用下面的公式表示

$$公式6：\mathbf{P}=\mathcal{M}(\mathbf{H} ; \mathbf{C}, \mathbf{A})=\mathcal{E}(\mathcal{S}(\mathbf{H}, \mathbf{C})) \mathbf{A}$$

其中函数$\mathcal{S}$被利用去测量每一个样本被分配到第j个中心的置信度$s_{ij}$。

$$公式7：s_{i j}=\mathcal{S}\left(\mathbf{h}_{i}, \mathbf{c}_{j}\right)=\frac{1}{1+\left\|\mathbf{h}_{i}-\mathbf{c}_{j}\right\|_{2}^{2}} \in \mathbf{S}$$

通过这种方式，当$\mathbf{h}_i$更加接近$\mathcal{c}_j$时，置信度$s_{ij}$会变高。函数$\mathcal{E}(\mathbf{S})$扩大每个样本的置信度到$[0,1]$之间，同时在他的$\left\{s_{i 1}, s_{i 2}, \ldots, s_{i K}\right\}$中最大时，增强了自信度。具体可用下面的公式表示：

$$公式8：s_{i j}=\mathcal{E}\left(\mathbf{s}_{i}\right)=\frac{\left(s_{i j} / \sum_{j} s_{i j}\right)^{2}}{\sum_{j}\left(s_{i j} / \sum_{j} s_{i j}\right)^{2}}$$

$\mathbf{A}$满足$\mathbf{A} \mathbf{A}^{T}=\mathbf{I}_{K}$，A是一个布尔矩阵，用于调整$\mathbf{S}$的范围。多视图的$\mathbf{P}$和$\mathbf{Q}^{v}$之间的交叉熵损失可以表示为下面的公式：

$$公式9：\mathcal{L}_{c o n}=\sum_{v=1}^{V} H\left(\mathbf{P}, \mathbf{Q}^{v}\right)=-\sum_{v=1}^{V} \sum_{i \in \mathcal{X}} \mathbf{p}_{i} \log \mathbf{q}_{i}^{v}$$

因为相同的$\mathbf{P}$是被所有视图共享的，公式9的优化可以得到多视图聚类的一致性$\left\{\mathbf{Q}^{v}\right\}_{v=1}^{V}$。第i个样本的聚类预测可以用下面的公式进行推理

$$公式10：y_{i}=\arg \max _{j} \sum_{v} q_{i j}^{v}$$

因为每个视图有他自己的聚类预测，并且不依赖于多视图的融合特征，所以经过本文的方法训练出的模型是不用融合的。

Optimization

本文提出的框架的损失函数由三个部分组成：

$$公式11：\begin{aligned} \mathcal{L} &=\mathcal{L}_{r e c}+\mathcal{L}_{c o m}+\mathcal{L}_{c o n} \\ &=\min _{\mathbf{C}, \mathbf{A},\left\{\mathbf{Z}^{v}, \mathbf{U}^{v}\right\}_{v=1}^{V}} \sum_{v=1}^{V}\left\|\mathbf{X}^{v}-f_{v}^{-1}\left(\mathbf{Z}^{v}\right)\right\|_{F}^{2} \\ &+\sum_{i \in \mathcal{X}} \sum_{j=1}^{K}\left\|\mathbf{h}_{i}-\mathbf{c}_{j}\right\|_{2}^{2}+\sum_{v=1}^{V} H\left(\mathbf{P}, \mathbf{Q}^{v}\right),\\ &\text { s.t. } \mathbf{P}=\mathcal{M}(\mathbf{H} ; \mathbf{C}, \mathbf{A}), \mathbf{A} \mathbf{A}^{T}=\mathbf{I}_{K}, \mathbf{Q}^{v}=\mathcal{M}_{v}\left(\mathbf{Z}^{v} ; \mathbf{U}^{v}\right), \end{aligned}$$

其中$\mathbf{Z}^{v}=f_{v}\left(\mathbf{X}^{v}\right), \mathbf{H}=\mathcal{H}\left(\left\{\mathbf{Z}^{v}\right\}_{v=1}^{V}\right)$。$\mathcal{L}_{r e c}$是自编码器的重构损失函数。$\mathcal{L}_{\text {com }}$和$\mathcal{L}_{\text {con }}$分别得到多视图互补性和一致性。

为了优化上面的不可微的目标函数，本文提出了交替优化策略如下：

初始化：首先深度编码器通过公式1进行初始化，并得到有意义的嵌入特征。然后聚类中心$\left\{\mathbf{U}^{1}, \mathbf{U}^{2}, \ldots, \mathbf{U}^{V}\right\}$通过使用K-means进行初始化。$\mathbf{A}$被初始化为$\mathbf{I}_{K}$。

P-step：固定$\left\{\mathbf{Z}^{v}, \mathbf{U}^{v}\right\}_{v=1}^{V}$并更新$\{\mathbf{P}, \mathbf{C}, \mathbf{A}\}$

首先$\mathbf{C}$通过优化公式5得到，他可以使用K-means进行有效地计算，让$l_{i}^{(t)}=\operatorname{argmax}_{j} s_{i j}^{(t)}$表示在第i次迭代中的聚类标签$\mathbf{h}_i$，在无监督的赏香吻中，通过$l_{i}^{(t+1)}$和$l_{i}^{(t)}$表示的聚类可能不一致。让$\tilde{m}_{i j}=\sum_{n \in \mathcal{X}} \mathbb{1}\left[l_{n}^{(t+1)}=i\right] \mathbb{1}\left[l_{n}^{(t)}=j\right]$，定义开销矩阵$\mathbf{M} \in \mathbb{R}^{K \times K}$，其中$m_{i j}=\max _{i, j} \tilde{m}_{i j}-\tilde{m}_{i j}$，并解决下面这个最大匹配问题：

$$公式12：\begin{array}{l} \min _{\mathbf{A}} \sum_{i=1}^{K} \sum_{j=1}^{K} m_{i j} a_{i j} \\ \text { s.t. } \mathbf{A} \mathbf{A}^{T}=\mathbf{I}_{K}, \end{array}$$

其中$\mathbf{A}\in \mathbb{R}^{K\times K}$是一个布尔矩阵，公式12使用匈牙利算法对公式12进行优化。

然后，$\mathbf{P}$可以通过映射$\mathcal{M}(\mathbf{H} ; \mathbf{C}, \mathbf{A})$，使用 $\mathbf{H}, \mathbf{C}$, $\mathbf{A}$作为输入进行直接计算。

Z-step：固定$\{\mathbf{P}, \mathbf{C}, \mathbf{A}\}$更新$\left\{\mathbf{Z}^{v}, \mathbf{U}^{v}\right\}_{v=1}^{V}$

给定固定的$\mathbf{C}$和$\mathbf{A}$，$\mathbf{P}$被当做所有视图的连续伪标签。公式11可以被分为$\left\{\mathcal{L}^{1}, \mathcal{L}^{2}, \ldots, \mathcal{L}^{V}\right\}$，其中$\mathcal{L}^{v}=\mathcal{L}_{\text {rec }}^{v}+\mathcal{L}_{\text {con }}^{v}=\left\|\mathbf{X}^{v}-f_{v}^{-1}\left(\mathbf{Z}^{v}\right)\right\|_{F}^{2}+H\left(\mathbf{P}, \mathbf{Q}^{v}\right)$。通过这种方式，每个视图的模型可以被独立学习。让$\lambda$ 表示学习率n表示batch size，可以通过使用最小批量梯度下降算法训练深度模型：

$$公式13：\begin{aligned} \mathbf{U}^{v} &=\mathbf{U}^{v}-\frac{\lambda}{n} \sum_{i=1}^{n} \frac{\partial \mathcal{L}^{v}}{\partial \mathbf{U}^{v}} \\ \mathbf{Z}^{v} &=\mathbf{Z}^{v}-\frac{\lambda}{n} \sum_{i=1}^{n} \frac{\partial \mathcal{L}^{v}}{\partial \mathbf{Z}^{v}} \end{aligned}$$

其中$\mathbf{Z}^v$通过更新神经网络中自编码器的参数来优化。

P-step过程通过从所有视图的嵌入特征中挖掘聚类胡必行来产生更精确的监督信息。Z-step使每个视图的模型利用监督信息学习更好的聚类嵌入特征。

算法1：DIMVC的优化

输入：数据集$\mathbf{X}^v\in \mathbb{R}^{N_v\times D_v}$，聚类数量K

输出：聚类预测

1. 初始化：通过公式1，初始化$\{\mathbf{Z}^v\}^V_{v=1}$。通过K-means聚类初始化$\{\mathbf{U}^v\}^V_{v=1}$，$\mathbf{A} =\mathbf{I}_{K}$
2. while 未达到最大迭代次数 do：
3. ​ P-step：固定$\left\{\mathbf{Z}^{v}, \mathbf{U}^{v}\right\}_{v=1}^{V}$
4. 通过公式5更新$\mathbf{C}$
5. 通过公式12更新$\mathbf{A}$
6. 通过公式6更新$\mathbf{P}$
7. ​ Z-step：固定$\{\mathbf{P}, \mathbf{C}, \mathbf{A}\}$
8. 通过公式13更新$\left\{\mathbf{Z}^{v}, \mathbf{U}^{v}\right\}_{v=1}^{V}$
9. end while

通过公式2和10计算聚类预测

Experiments

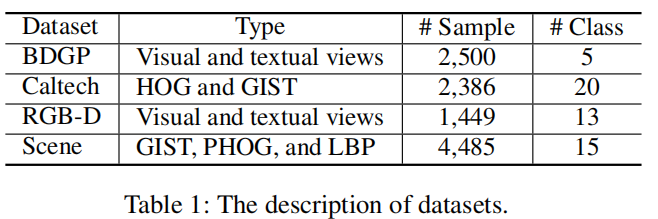
数据集信息如下表：

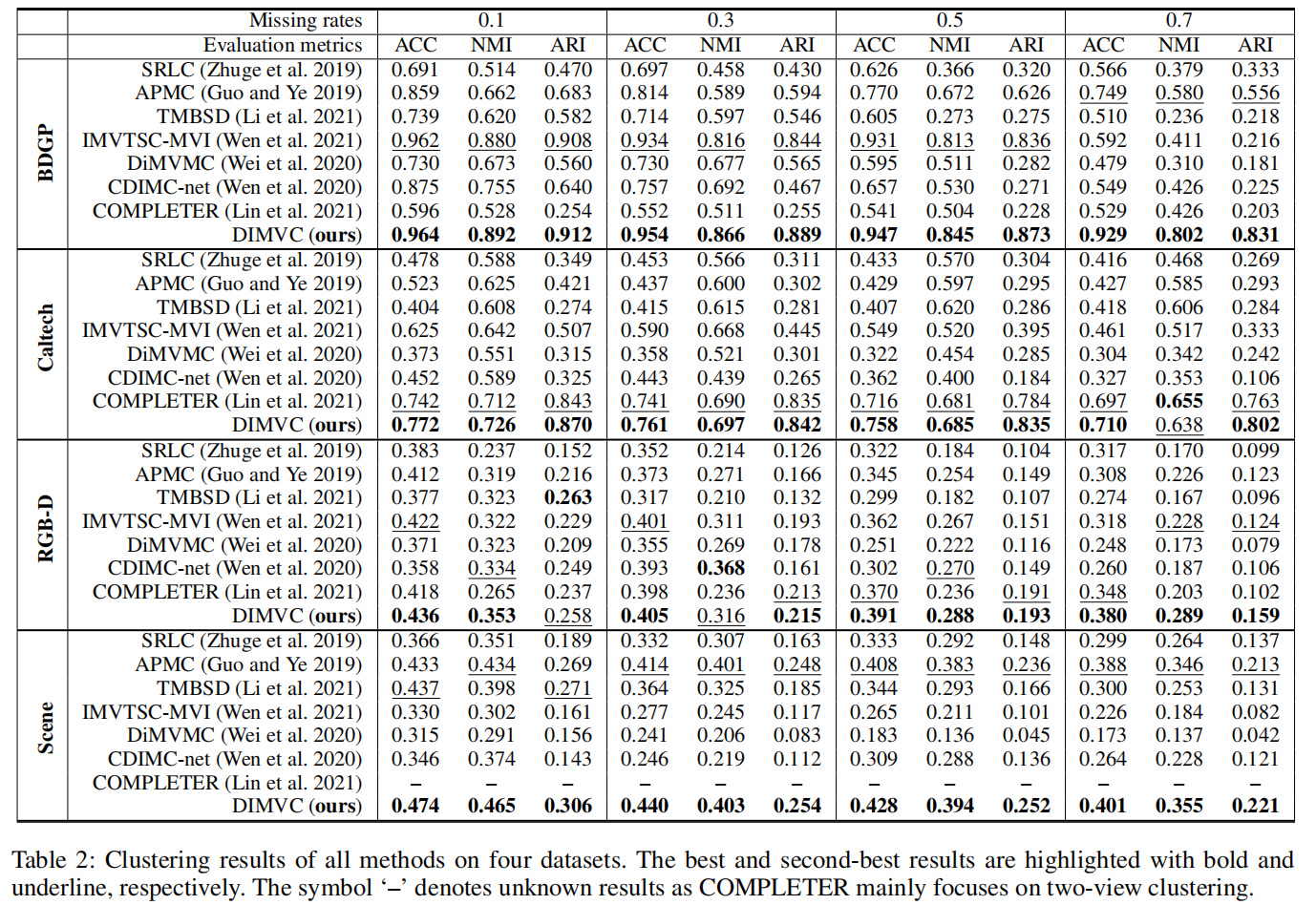
在数据集上对比的方法实验结果如下表：

1. DIMVC在所有数据集中都具有最好的表现。
2. 在丢失率(missing rate)从0.1变化到0.7时，所有方法的聚类表现，而DIMVC在大部分情况下仍然保持较好的聚类效果。

原因：

1. 如果多视图数据的丢失率变高，多视图中的互补信息变少。这是所有方法聚类质量下降的原因
2. 归类方法需要数据分布的估计，因此当丢失率变高时，计算误差增大。
3. 融合方法会受到低质量视图的影响，尤其是不完整多视图学习。

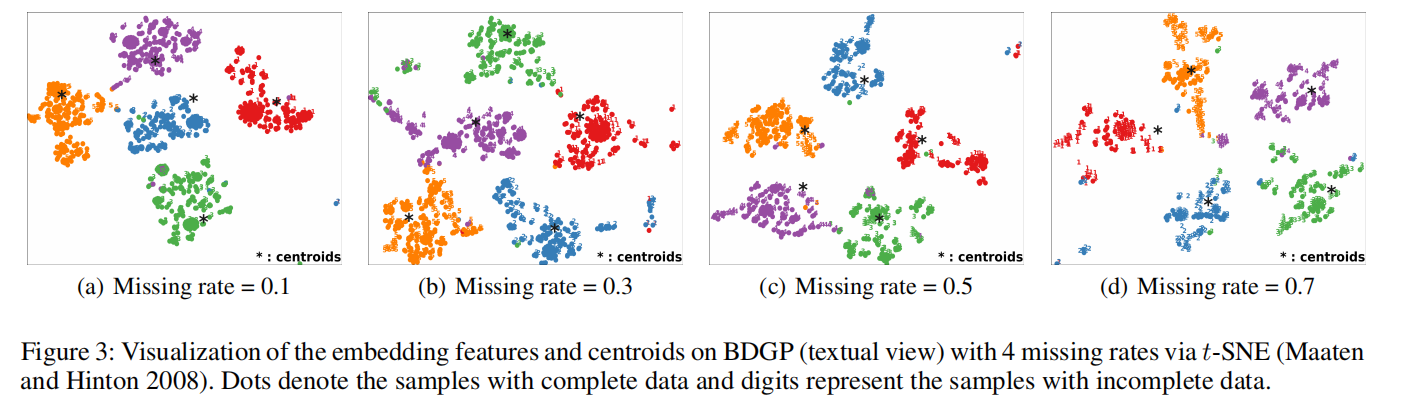
学习嵌入特征和中心的过程如下图：