「论文阅读」Multi-view clustering A survey

论文名称：Multi-view clustering: A survey

作者：Yan Yang; Hao Wang

时间：2018

期刊或会议：Big Data Mining and Analytics

Introduction

举一些例子说明什么是多视图数据：

分享到网站的图片通常有对应的文字标签和描述
特定的新闻通常由不同的新闻机构报道
传感器信号会在时域和频域上分解
相同的语义可以被多个语言表达

聚类是一个有力的用于探索数据的底层结构的交替学习工具。他的基本思想是，根据某种要求对一组数据进行分类，使得相似物体尽可能分配到相同的簇中，而不相似的物体尽可能分配到不同的簇中。

多视图聚类的目标利用多个视图的互补信息和共同信息是，从而提取出多视图数据中更高质量的特征。

今年来聚类算法表现很好，但是大多数都只在一个视图上，而对于多视图数据则是将他们叠加到一个单一的视图上再使用优秀的聚类算法进行聚类，但这通常不能促进多视图聚类的效果，由于每一个视图有其特定的统计属性，所以这种方法并没有物理意义。

找到一个方式去最大化每一个视图的聚类质量同时考虑多个视图的聚类一致性是在MVC（多视图聚类）的全程中需要被精心设计去解决的固有问题。此外，不完整的多视图数据（某些视图无法被观察，或者部分视图的特征无法使用）也是MVC的一个挑战。

综述中提到的分支方法如下

$\begin{cases} 协同训练算法\\ 多核学习\\ 多视图图聚类 \begin{cases} 基于图(graph-based)\\ 基于网络(network-based)\\ 基于频谱(spectral-based)\\ \end{cases}\\ 多视图子空间聚类 \begin{cases} 基于子空间学习\\ 基于非负矩阵分解 \end{cases}\\ 多任务多视图聚类\\ \end{cases}$

协同训练算法：使用协同策略来处理多视图数据，它通过使用先验知识或彼此之间的学习知识来引导不同视图聚类。通过迭代执行这个策略，所有视图的聚类结果互相趋近，从而获得所有视图最广泛的公共语义。
多核学习：使用对应于不同视图的预定义内核，然后将这些内核线性或非线性地组合起来，以提高聚类性能。
多视图图聚类：寻找在所有视图中找到一个融合图(fusion graph)(或网络)，然后在融合图上使用图切(graph-cut)算法或其他技术实现聚类效果
多视图子空间聚类：从所有视图的所有特征空间中，学习一个统一的特征表示（假设所有的视图都共享这一表示）。典型模型包括：子空间学习和非线性矩阵分解(NMF)
多任务多视图聚类：使用一个任务或多个相关任务来处理每个视图，将任务间的知识转移到彼此之间，并利用多任务和多视图关系来提高集群性能。

符号定义：

符号	意义
$k$	用户指定的聚类数量
$m$	视图数量
$n$	实例数量
$n_v$	在v视图的实例数量
$d_v$	在v视图的维度
$X$	$X = \{X^1,...,X^m\}$ ，有m个视图的数据矩阵
$X^v$	第v个视图的数据矩阵
$x_j^v$	$X^v$ 的第j列向量
$x_{ij}^v$	$X^v$ 在 $(i,j)$ 的元素
$I$	单位矩阵

如果多视图数据是完整的，那么 $n=n_v$

Principles of MVC

MCV最重要的两个原则：互补性和一致性

如下图：

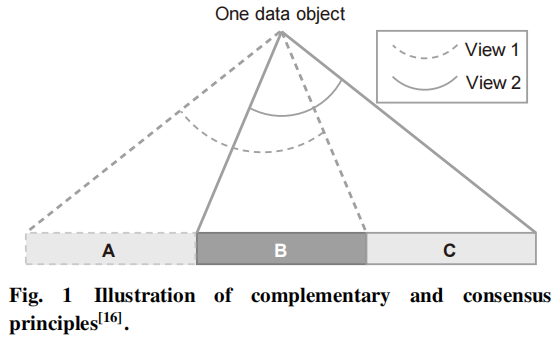
给定一个拥有两个视图的数据对象，这个数据对象被映射到一个潜在的数据空间中，数据对象一部分(A和C)存在与独立的视图中，比如A的在视图1中，C在视图2中，这就是互补性。数据对象的一部分(B)被所有视图共享，这就是两个视图的一致性。

互补性原则：为了更全面，更准确地描述数据对象，应该采用多个视图进行描述。对于单一视图可以针对某个知识发掘任务进行处理，但是不同视图包含着彼此之间的互补信息。比如图像处理中，可以用不同类型的特征描述图像，如LBP,SIFT和HOG。其中LBP有强大的纹理特征，SIFT使得图像的光照，噪声，旋转更加鲁棒，HOG对图像的边缘信息敏感。因此，利用这些互补信息去描述数据对象是非常必要的，这可以对聚类内部提供更深刻的见解。

一致性原则：这个原则的目的是最大化多个不同视图之间的一致性。基于可能性的近似正确分析，提出了一种对一致性原则的返回误差分析方法。给定一个多视图数据集 $X$ ，这个数据集有两个视图 $X^1$ 和 $X^2$ 。在一些合理假设下，之前的研究工作中证明了两种假设在两种视图上一致性之间的联系，这种联系可以使用公式1表示：

$公式1：P\left(f^{1} \neq f^{2}\right) \geqslant \max \left\{P_{\mathrm{err}}\left(f^{1}\right), P_{\mathrm{err}}\left(f^{2}\right)\right\}$

通过这个不等式可以得出结论：在两个独立独立假设上的不一致误差概率(error probability)是一个假设的错误率的上限。因此最小化两个假设的不一致将使得每一个假设的错误率最小化。换句话说，最大化两个假设的一致性将使每个假设的错误率最小。即maximizing-consistence策略。

Multi-view Clustering

Co-training style algorithms

协同训练的算法在考虑多视图的一致性时被提出。这类方法打算最大化所有视图的相互一致并且得到了最广泛的一致性。常规的协同训练算法的一般过程如下图：

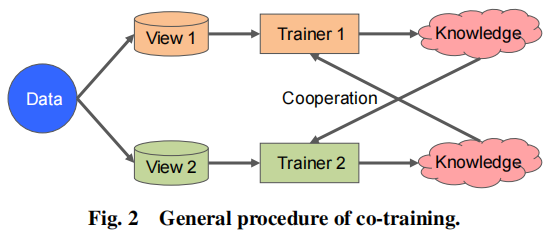
从图中可知，算法是交替训练的，其目的是通过先验知识和从彼此中学习到的知识最大化两个不同视图的一致性。成功的协同学习方法通常依赖下面3个假设

充分性：每一个视图都足以单独地完成学习任务
兼容性：目标函数对在两种视图中以高概率同时出现的特征输出有相同的预测
条件独立性：在条件独立的情况下，所有的视图都提供了的学习标签

但是要满足条件独立假设通常是困难的，于是一些更弱的假设被踢出来，比如：弱条件依赖假设，更弱的扩张假设，不同假设。此外，一些协同训练的拓展版本也被提出来，比如，co-EM，协同正则化(co-regularization)以及协同聚类(co-clustering)。

上述提到的方法，大多是半监督学习的，对于无监督学习，Bickel和Scheffer第一次根据协同学习的思想，提出了两种用于文本数据的MVC算法。

一个是在视图中交替执行的多视图EM算法
另一个是由协同训练算法启发的凝聚算法(agglomerative algorithm)

他们得出结论，EM算法在单视图上表现出色，而凝聚算法则导致了一个消极的结果。

之后，他们通过证明EM算法是一种特殊的混合模型估计，使得应用混合模型估计有助于多视图数据的分析。

后面其他研究人员提出了一种加权多视图凸混合模型，该模型通过EM自动地为视图分配权重。

假设相似的数据，不管视图如何都会被分组到相同的簇中，研究人员提出了一种用于多视图谱聚类的协同训练方式，其中簇通过使用另一个视图的互补信息引导不同的视图。此外，有人进一步提出用于多视图谱聚类的协同正则化方法，其中图拉普拉斯被强加在所有视图上，并对拉普拉斯的特征向量进行正则化，以一致地引导得到聚类结果。

受到之前工作的启发，又产生了用于MVC的协同正则化核K-meas方法。这种方法自动地从数据中学习不同视图的权重。此外，又提出了具有协同训练策略的多视图感知方法来聚类执行过程，该方法认为时间日志的轨迹由多个轨迹轮廓描述，将其使用协同训练的方式迭代执行，从而挖掘过程信息。

后面又提出了一种用于MVC的协同正则化的概率潜在语义分析（PLSA）。他的中心思想是：以个视图中的主体空间相似样本应该与另一个视图的主体空间相似样本一致。

为了解决不完整视图带来的挑战，提出了使用成对协同EM算法约束传播的多视图约束聚类。其使用协同EM算法去迭代估计在每一个视图的传播，跨视图传输给定成对约束，更新聚类模型，最后学习所有视图上的统一聚类结果。

基于协同聚类的MVC方式（同时聚类对象和特征）也被提出。

异构数据的协同聚类方法：其没有值从两个视图延伸融合，而是给多个数据源的特征进行加权。
近似交替线性最小化算法（基于矩阵分解的方法）：同时分解多个数据矩阵到系数的行和列向量中，使用二值向量连接不同的数据视图，其中二值向量强制使得来自所有的行簇保持一致性。
学习多视图数据协同相似性的结构：其假设将相似值(从独立的数据中生成)从一个视图转化到另一个视图可以得到更好的数据聚类。拓展基于协同相似性的体系结构，以便用两种集成方案来处理多个数据集(中期整合和后期整合)这个类型的方法通常有两个阶段：本地阶段和协同阶段
1. 本地阶段在每个视图上运用聚类算法
2. 协同阶段将每个视图与从本地阶段生成的其他视图相关联的聚类结果进行协作。
在这一类方法中，有人提出从一个视图中进行频谱嵌入(spectral embedding)以约束另一个视图的相似度图，通过迭代地执行这个过程，两个视图的聚类相互趋近。
举个例子(使用两个视图)：
1. 计算所有视图的图相似性矩阵 $S^1$ 和 $S^2$
2. 初始化图拉普拉斯矩阵 $L^1$ 和 $L^2$ ，判别特征向量 $U^1$ 和 $U^2$
3. 利用 $U^2$ 对 $S^1$ 进行频谱嵌入，得到新的相似矩阵 $S^1$
4. 利用 $U^1$ 对 $S^2$ 进行频谱嵌入，得到新的特征矩阵 $S^2$
5. 计算新的拉普拉斯矩阵 $L^1$ 和 $L^2$ ，新的特征向量 $U^1$ 和 $U^2$
6. 回到步骤3，重复一定的迭代次数

Multi-kernel learning

为了实现良好的泛化，多核学习最初是为了提高可能的核函数搜索空间能力而开发的，比如线性核，多项式核，高斯核等。由于多核学习中的核自然地对应于不同的视图，因此多核学习对应于不同的视图，因此多核学习在处理多视图数据中得到了广泛的应用。多核学习的生成过程可以用下图表示：

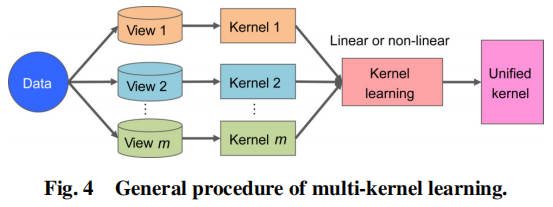
多核学习的MVC方法倾向于最优化地组合一组预定义的核，以促进聚类效果。因此就产生了一个基本问题：找到一个方法去选择合适的核函数以及组优化地组合这些核。

假设只有单一的视图，基于最大化边界聚类

有人提出了一种多核聚类算法，其可以同时找到超平面的最大边界，最好的聚类以及最优化的核。
有人提出在核空间上使用具有鲁棒性的K-means（使用 $l_2,l_1$ 正则化）方法，并提出了一种多核K-meas方法，其能够同时找到最好的聚类标签，聚类成语移进最优的多核组合。

在多视图的假设下

有人构建一种基于最小化不一致(minimizing-disagreement)算法，具体来说，他们生成一个多部图，以引导一个核，然后用于谱聚类。事实上，这个方法可以看做是和规范相关分析的一种变体，也是协同聚类和谱聚类的一种推广。
有人将经典的K-means聚类拓展到希尔伯特空间，其中将多视图数据矩阵表示为表示为核矩阵，然后自动合并进行数据融合。

为了更好地捕获数据的样本特征，提出了一种局部组合内核的方式

有人研究了基于中心核对齐的多核聚类(一种有效地和估计测量)，将两个聚类任务和多核学习统一到一个单一的优化框架中。

考虑到视图(或核)的差异，也研究了采用核加权组合的方法。

基于核的加权MVC方法，其根据相应视图的信息质量分配给核权重。
为了实现自动分配在每个视图上推导核矩阵的权重，一个系统的MVC方法被提出，其中，核矩阵学习是基于核对齐的，以便于测量两个核矩阵之间的相似性。
一种基于矩阵引导正则化的加权多核K-means聚类方法被提出，其能够减小核荣誉，增强预定义核的多样性
基于矩阵引导和低级正则化的加权MVC方法
基于变量权重促进高斯核的加权MVC算法

在不完整的多视图聚类中

有人提出了一种通用的方法，允许在完整视图中的MVC方法使用于不完整的场景，其中只有一个视图是完整的，而辅助视图是不完整的。他们使用基于CCA核的MVC为例说明了他们的想法。

在没有视图完整的情况下：

有人提出了一种公共核学习算法(collective kernel learning algorithm)，以便于推断隐藏样本的相似性。这种方法背后的思想是通过优化这些视图共享实例的对齐方式来集中完成不完整视图的核矩阵。
与现有的一些方法不同，首先对输入采用多核聚类算法，再将核计算和聚类集成到不完整的多视图聚类的统一学习过程中。

多核学习的一个挑战是选择合适的核函数，其映射了原始低维空间到高维空间。通用的多视图聚类方法应该是使用多个核函数的线性组合，其中不同核的权重应该被考虑。此外，不同视图的权重也是MVC任务的一个影响因子。有人研究了一种自动加权的多核MVC算法，其可以同时加权视图和核。下图给出了这个算法的流程：

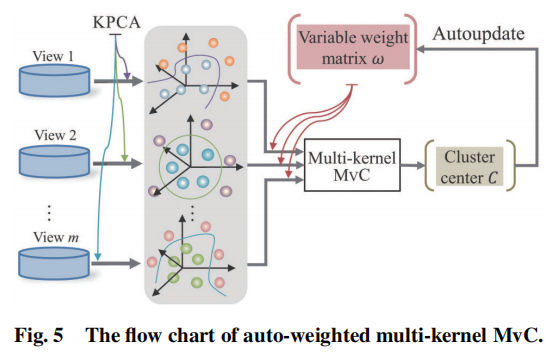
首先在每一个视图上使用核主成分分析(KPCA)，以减少原始数据的维度，从而得到低维的多视图数据。然后在低维多视图数据中使用设计好的加权高斯核。这个过程驱动每个视图和聚类中心的权重。经过有限次迭代之后，得到了最终的聚类结果。设计好的加权高斯核同时包括高斯核和多项式核的优点，设计好的加权高斯核可以用下面的公式表示：

$公式2：\begin{array}{c} K(x, y)=\left[\exp \left(-\frac{\|x-y\|^{2}}{2 \sigma^{2}}\right)+R\right]^{p}= \\ \sum_{q=0}^{p}\left(\begin{array}{c} p \\ q \end{array}\right) R^{p-q} \exp \left(-\frac{q\|x-y\|^{2}}{2 \sigma^{2}}\right)= \\ R^{p}+\sum_{q=0}^{p}\left(\begin{array}{l} p \\ q \end{array}\right) R^{p-q} \exp \left(-\frac{\|x-y\|^{2}}{2 \sigma^{2} / q}\right) \end{array}$

给定多视图数据有m个视图，n个样本和k个簇，基于K-means和设计核的目标函数可以用下面的公式表示：

$公式3：\begin{array}{l} \min \sum_{v=1}^{m} \sum_{i=1}^{n} \omega_{i, v} \sum_{j=1}^{k} \delta_{i j}\left\|\phi^{v}\left(x_{i}^{v}\right)-\phi^{v}\left(c_{j}^{v}\right)\right\|^{2} \\ \text { s.t., } \omega_{i, v} \geqslant 0, \prod_{v} \omega_{i, v}=1 \end{array}$

其中 $c_j^v$ 是聚类中心， $\delta_{i j}$ 是指示变量，如果 $x_{i} \in c_{j}$ 则 $\delta_{i j}=1$ ，否则 $\delta_{i j}=0$ 。

通过将设计好的高斯核 $K(x, y)=\phi(x) \cdot \phi(y)$ 插入到公式3中，可以得到

$公式4：\begin{array}{l} \min \sum_{v=1}^{m} \sum_{i=1}^{n} \omega_{i, v} \sum_{j=1}^{k} 2 \delta_{i j}\left[(1+R)^{p}-K\left(x_{i}^{v}, c_{j}^{v}\right)\right] \\ \text { s.t., } \quad \omega_{i, v} \geqslant 0, \quad \prod_{v} \omega_{i, v}=1 \end{array}$

公式4继承了K-means和核的属性，所以设计的核集成了高斯核和多项式核的优点。

Multi-view graph clustering

图被广泛应用于表示对象间的关系，其中每个节点对应一个数据对象，每条边描述一对对象之间的关系。在实际中，这种关系通常由相似度或者亲和关系来表示，即，输入的图矩阵是由数据的相似矩阵生成的。

在多视图的假设中，可以通过多个图来捕获数据对象。每一个独立的图能够捕获数据的部分信息，所有的图有相同的数据的底层聚类结构。这些图能够通过共同地巩固数据对象之间的合作从而实现相互加强。总的来说，用于多视图数据的基于图融合的过程如下图所示：

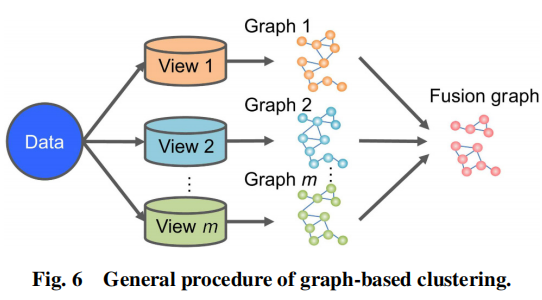
多视图图聚类的目的是找到一个所有视图的融合图，然后在融合图上使用图切(graph-cut)算法或其他技术（谱聚类）来产生最后的聚类结果。这种类型，主要有三种：基于图的MVC，基于网络的MVC，基于频谱的MVC

Graph-based MVC

基于多个相似图，有人提出的链式矩阵分解方法从多个视图中提取公因子，从而产生了各种基于图的聚类方法，可以自然地应用与多视图数据。

多视图文档聚类算法：首先对每个视图的数据矩阵应用单视图聚类算法，以生成多个部分。然后使用这些分区去生成一组三个不同的相似矩阵，分别叫做，亲和力矩阵，基于聚类的相似矩阵，成对不相似矩阵。最后使用集成技术对这些矩阵进行聚合，形成统一的相似矩阵进行聚类。
此外Pearson相关系数，Spearman相关系数，欧几里得距离和堪培拉距离等度量方式，都可以对这类方法产生一定影响。
分组感知多视图融合方法：采用不同的权重来表征不同组之间的两两相似性。
不用参数的多图框架：其自动地从所有图中学习一组权重。

多视图数据的无监督特征选择也被提出，这些选择出来的特征也用于聚类任务和其他学习任务中。

基于特征选择的交叉扩散矩阵对齐：通过在一个交叉扩散矩阵中进行对齐来从每一个视图中选择特征。然后在这些选择的特征上采用协同正则化谱聚类来产生最终的结果。
多视图无监督特征选择算法：其能够自适应相似度和视图权重

总的来说，特征选择方法采用了三种数据信息：数据相似性，数据聚类结构，不同视图之间的相关性

多模态聚类的多资源共享最近邻(SNN)机制：核心思想是将现有的基于SNN的相似性度量扩展到多个源的情况下，然后引入一个原始的自动源选择步骤来构建候选聚类。
用于MVC的集成流形(manifold)正则化生成模型：为每个视图构建了最近邻图，以编码对应的流形信息，为了学习最优的内部流形，涉及了一个多图集成正则化框架。之后流形正则化项被使用到了基于PLSA的多视图模型中，得到了一个统一的目标函数
基于重点是为MVC有效筛选聚类一致性邻居的研究，提出了一个方法，通过将每个对象用每个视图下的邻居加权和表示来过滤特定邻域并集中不可靠的邻居。学习到的稀疏权重被用于去是生成一个相似图，这个图被进一步用于MVC。
带有自适应邻居(adaptive neighbors)的新颖的多视图学习模型：这个模型同时进行半监督分类和局部流形学习和聚类。在每轮迭代中其修改相似矩阵，直到获得最优的相似矩阵。此外，其自动地为每个视图分配权重系数，而没有惩罚参数。

现有的方法大都使用整个数据空间中的全局统一的相似度量，而显示物体中，比如图像，不同的图像具有不同的视觉外观，视觉分布也很复杂，只使用全局统一度量很难准确地捕获不同物体的相似性。为了解决这一问题，一种用于图像聚类的分组感知多视图融合方法被提出。该方法可以将图像划分为不同的更具紧凑的视觉内聚性的组中，并未组间和组内的图像分配不同的融合权值。对比与全局融合方法，这个分组感知融合模型提供了更灵活的融合策略以及所有图像中更多有效的相似度量。这个方法的框架如下图所示：

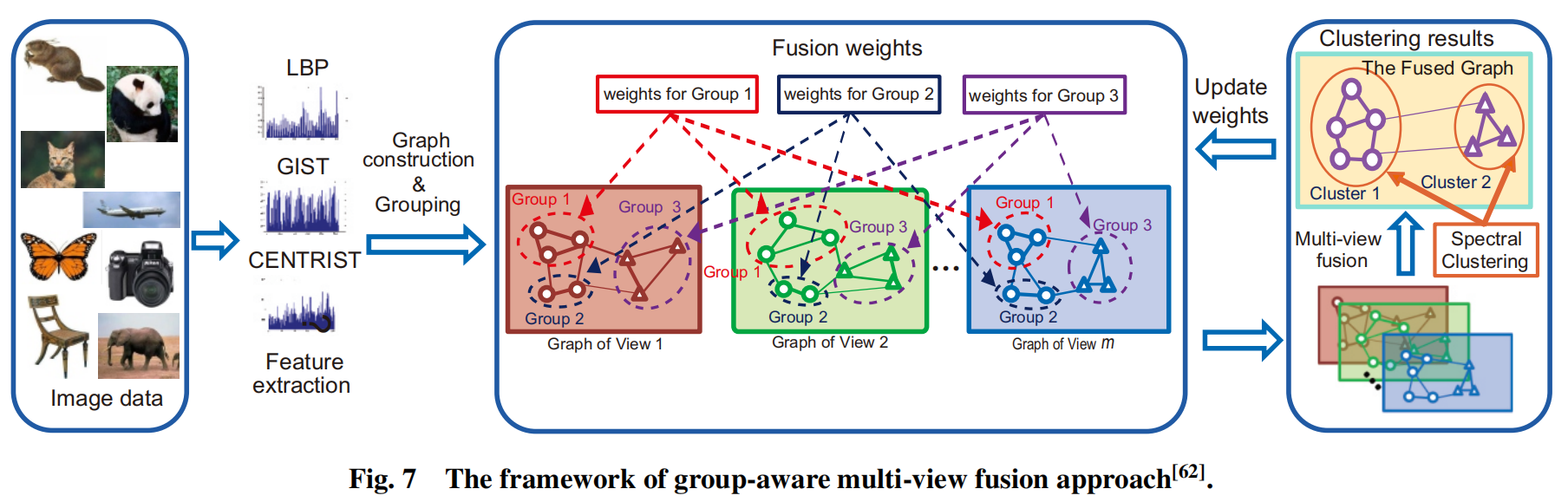
多个特征，如LBP,GIST和Centrist被从图像中提取，并形成三个不同的特征(视图)。然后在每一个视图上构造一个图，并使用提出的融合策略构造一个融合图。目的是为属于不同组的图像分配不同的融合权重，为同一组内的图像分配相同的融合权重。最后通过求解目标函数来学习融合权值，并通过对融合图进行谱聚类得到聚类结果。

Network-based MVC

大部分基于图的MVC方法假设相同数据对象集合在不同的视图上都是可用的，因此不同视图上的数据对象之间的关系是意义对应的，但是在许多现实应用中，比如社交网络，文献引用网络以及生物学相互作用网络中，数据从不同的领域中收集而来，一个领域中的一个对象对应另一个领域中的多个对象，从而出现了多对多映射的关系。因此使用网络来表示这些关系可能会更合适一些。

协同正则化图聚类（基于网络的多视图图聚类框架）：这个框架说明了几个重要的属性，分别为：多对多映射关系，与权重关联的映射，所有不同网络中的部分映射。由于不同网络有不同的数据分布，这使得所有的网络拥有相同的聚类结构的假设不再成立。
为了减小这个假设带来的影响，提出了一种鲁棒且灵活的框架：其允许多个底层聚类结构跨越不同的网络。其将域相似性作为主网络，然后通过在设计好的网络上使用NMF来解决聚类问题。(这个小节后面详细说明)
现有的基于网络的方法倾向于关注网络聚类任务本身，而忽略了来自不同领域的聚类结果之间可能表现出的关联。于是有人提出了一个鲁棒的聚类方法，其能够在多个领域中检测网络聚类以及他们跨域的联系。
有人研究了在多个社交网络中进行社区检测，并试图同时找到设计anchor用户和non-anchor用户的多个网络工作的社区。
基于最大乘积新来传播的多视图亲和传播方法：其关键点是建立一个由试图内质量度量和不同视图之间的显示聚类一致性组成的MVC模型。

在这个类型的第二个方法中，其建模每个域的的相似性为一个网络，并建模其他域的相似性为一个网络，以规范不同网络中的聚类结构。他们定义了一个名为Network of Networks(NoN)的全局网络，如下图所示。

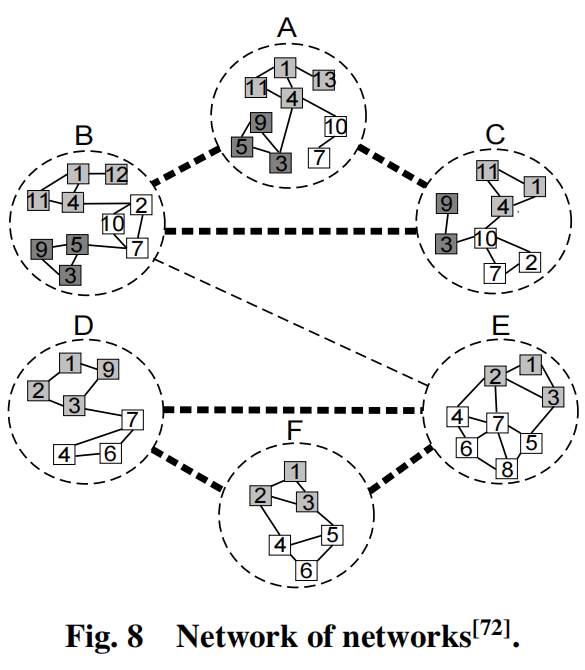
其中虚线网络表示6个域 $\{A,B,C,D,E,F\}$ 之间的主网络，主网络中的每一个节点对应特定域网络（其内部的节点用实线链接）。主网络和特定域网络的聚类分别被称为主聚类和域聚类。作者视图使用来那个阶段的方法来划分网络，在这个方法中，首先主网络被划分，然后学习信息从主网络中整合以便于聚类特定域网络。目标函数可以用下面的公式表示：

$公式5：O_{M}=\left\|G-H H^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}$

其中 $\|\cdot\|_{F}^{2}$ 是Frobenius范式， $G \in \mathbb{R}^{g \times g}$ (g是主网络中的节点数量)是主网络， $H \in \mathbb{R}_{+}{ }^{g \times k}$ 是主网络的因子矩阵(factor matrix)

域网络聚类可以用下面的公式表示：

$公式6： \min _{\substack{\forall i, U^{i} \geqslant 0 \\ \forall j, V^{j} \geqslant 0}} O_{S}= \begin{aligned} &\underbrace{\sum_{i=1}^{g}\left\|A^{i}-U^{i}\left(U^{i}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}}_{\text {Domain-specific network clustering }}+ \\ & \alpha \underbrace{\sum_{i=1}^{g} \sum_{j=1}^{k} h_{i j}\left\|U^{i}-V^{j}\right\|_{\mathrm{F}}^{2}}_{\text {Main cluster guided regularization }} \end{aligned}$

其中 $A^{i}$ 是域网络中对应主网络 $G$ 中的点 $i$ （ $i=1,...,g$ )。 $U^i$ 是 $A^i$ 的因子矩阵。 $V^j$ 是第j个隐藏的因子矩阵， $h_{ij}$ （ $H$ 的一股元素）表示主节点 $i$ 属于第 $j$ 个主聚类的程度。 $\alpha$ 是正则化参数。

基于上面提出的模型，他们设计了一个生成网络，允许部分对齐的特定域网络具有不同的节点大小和不同数量的聚类。这个模型可以用下面的公式表示：

$公式7：\min _{\substack{\forall i, U^{i} \geqslant 0 \\ \forall j, V^{j} \geqslant 0}} O_{S}=\sum_{i=1}^{g} J_{A}+\alpha \sum_{i=1}^{g} \sum_{j=1}^{k} J_{R}$

其中

$\begin{array}{l} J_{A}=\left\|A^{i}-U^{i}\left(U^{i}\right)^{T}\right\|_{\mathrm{F}}^{2}, \\ J_{R}=\left\|\left(Q^{i j} U^{i}\right)\left(Q^{i j} U^{i}\right)^{\mathrm{T}}-\left(P^{i j} V^{j}\right)\left(P^{i j} V^{j}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}, \end{array}$

$P^{ij}$ 是 $U^{i}$ 和 $V^{j}$ 之间的映射矩阵， $Q^{i j}=P^{i j}\left(P^{i j}\right)^{\mathrm{T}}$ ，最后，聚类结果是在因子矩阵 $U^{i}, \ldots, U^{g}$ 上驱动的。

Sepctral-based MVC

谱聚类是一种经典的数据聚类方式。其基本思想是在任意一个对象数据对之间形成一个成对的亲和力矩阵，故意华这个亲和力矩阵，然后计算这个亲和力矩阵(图拉普拉斯)的特征向量。归一化的图拉普拉斯的的特征向量是二值向量解的松弛。(the second eigenvector of the normalized graph Laplacian is a relaxation of a binary vector solution.)这个解可以最小化图上的归一化起个，即频谱和图之间的关系。

在两个独立视图上的谱聚类算法，每个视图都可以输入一个聚类模型：其创建了一个具有最小化不一致（minimizing-disagreement）准则的二分图，以便于连接两个视图的特征，然后在这个二分图上执行可用的谱聚类算法
有人研究了多视图谱聚类，将但视图的归一化切割推广到多视图聚类中，考虑瑞和学习更接近所有图最优解的聚类，并进一步发展在多视图谱聚类的基础上的多视图转换的推理。
分布式框架下的多图无监督学习通用模型：其目的是从每一个视图的表示中单独地检测隐藏的模式(patterns)，从这些模式中寻找最佳的隐藏模式。z作者提出了映射函数的感念，以使来自不同模式空间的模式在这个通用模型中具有可比性。因此，这些不同的多重表示模型获得了一个最优的模式。
几种非冗余聚类方案：这个方法在多个视图上学习非冗余子空间，在每一个视图上同时产生一个聚类结果。
为了解决数据可能包含噪声的问题，提出了Markov链去建立一个多视图的谱聚类模型。该模型具有低秩，稀疏分解的特点。其首先从每一个单一的视图中绘制转移可能性矩阵(transition probability matrix)，然后使用这些矩阵取形成一个共享的低秩转换可能性矩阵。最后这个共享的矩阵输入到一个标准的用于聚类的Markov链模型中。
为了处理大规模问题，提高计算效率，提出了一个用于大规模多视图数据的多视图谱聚类：其使用一个本地流形融合去融合异构特征，使用二分图近似相似图。
基于频谱划分和局部细化的无参数归一化多视图谱聚类算法
通过在每一个单一视图上研究使用稀疏正则化的凸稀疏谱聚类，提出了一个用于处理多视图数据的成对的系数谱聚类
随着视图的变多，几乎不可避免视图之间的依赖关系，而且这些依赖关系通常会掩盖正确的预测结果。为了解决这一问题，有人拓展了传统谱聚类，以便于处理视图间的依赖。他们设计了一个头脑风暴过程，以使每个视图的信息被他们分享。
通过将谱聚类拓展到具有多个可用的亲和度，开发了一种亲和聚合谱聚类算法。
基于带有不同源差异惩罚的协同谱聚类的多源MVC框架，值得注意的是这个应用可以用于不完整的多视图数据
通过使用鲁棒的子空间学习的多视图谱聚类：其考虑到所有视图都是有噪声的，并且来自于一个鲁棒的统一子空间和噪声。
用于多视图谱聚类的迭代低秩(low-rank)的结构优化方法：其编码了从每一个对立视图特征空间中编码数据的局部流形结构，并打成一个基于迭代过程多视图协作(multi-view agreement)。
具有成对相似度矩阵的多视图矩阵补全方法(半监督MVC)：其利用边的信息，称为must-link和cannot-link

有很多基于频谱的MVC方法用于多类关系数据，多模态图像数据，社交媒体数据。也有很多使用基于频谱MVC方法的应用，比如：多模态类脑网络推理(multimodal brain network inferences)，社交圈检测(social circle detection)以及人类微生物数据分析(human microbiome data analysis)。

总体来说，谱聚类方法包含两个比较花费时间的步骤：一个是构造相似度(亲和度)图，时间复杂度为 $O(n^2d)$ 。另一个是计算特征分解，时间复杂度为 $O(kn^2)$ 。

谱聚类存在的另一个缺点是：大多数谱聚类方法通常不能为处理外部样本提供一个合适的拓展。为了解决这些问题，有人提出了一种用于大规模多视图数据的多视图谱聚类方法。

其使用局部流形正则化来融合异构特征，使用二分图近似相似度图去提高有效性。首先其从所有视图中生成一些公共的显著点，这些显著点被使用去捕获原始视图的流形。然后为每一个视图构建一个原始数据点和显著数据点之间的二分图。所有视图的图通过使用局部流形正则化项进行融合。最后，使用在融合图上使用谱聚类算法，并输出突出点的聚类指标，从而有效地解决了外部样本的问题。

这里有两个重要的问题需要强调

如何得到跨所有视图的一致性
如何表达他们之间的关系

通过局部流形学习，这两个问题可以用下面的公式表示：

$公式8：\begin{aligned} \min _{F^{\mathrm{T}} F=I, \alpha^{v}} & \sum_{i=1}^{m}\left(\alpha^{i}\right)^{r} \operatorname{tr}\left(F^{\mathrm{T}} L^{i} F\right), \\ \text { s.t., } \sum_{i} \alpha^{i}=1, \alpha^{i} \geqslant 0 \end{aligned}$

其中 $\alpha^{i}$ 是第i个视图的非负归一化权重因子， $\operatorname{tr}(\cdot)$ 是矩阵的迹， $r$ 是一个用于控制不同视图之间不同权重值分布的标量。 $F \in \mathbb{R}^{n \times k}$ 是类指标矩阵， $L^{i}$ 是第i个视图的归一化图拉普拉斯的矩阵。归一化图拉普拉斯矩阵可以用下面的公式表示：

$公式9：L=I-D^{-1 / 2} W D^{-1 / 2}$

其中 $W \in \mathbb{R}^{n \times n}$ 是图的邻接矩阵(adjacent matrix)， $D \in \mathbb{R}^{b \times n}$ 是第i个对焦元素为 $d_{i i}=\sum_{j=1}^{n} w_{i j}$ 的程度矩阵。

公式8的目的是提供所有视图中的一致性结果 $F$ ，这种独特的公式消除了对计算每个视图的局部结果的要求，也消除了在局部结果和全局结果之间来回通信的计算开销。为了进一步揭示视图之间的关系，公式8可以改写为：

$公式10：\begin{array}{l} \min _{F^{\mathrm{T}} F=I, \alpha^{v}} \operatorname{tr}\left(F^{\mathrm{T}} L F\right), \\ \text { s.t., } \sum_{i}^{m} \alpha^{i}=1, \alpha^{i} \geqslant 0 \end{array}$

其中 $L=\sum_{i}^{m}\left(\alpha^{i}\right)^{r} L^{i}$ ，表示 $L$ 被认为是所有视图的局部流形融合，公式10可以使用迭代优化技术进行解决，总体计算复杂度大约为 $O\left(T k n^{2}+\right.\left.\sum_{i}^{m} m n\left(d^{i}\right)^{2}\right)$ ，其中 $T$ 是迭代次数。

Multi-view subspace clustering

多视图子空间聚类已经变成了MVC领域的一个热点主题。其在多视图数据中学习一个全新统一的表示，这个表示来自多个子空间，或一个潜在的空间，使其在构建聚类模型时更容易处理高维数据。多视图子空间聚类的过程通常流程如下图：

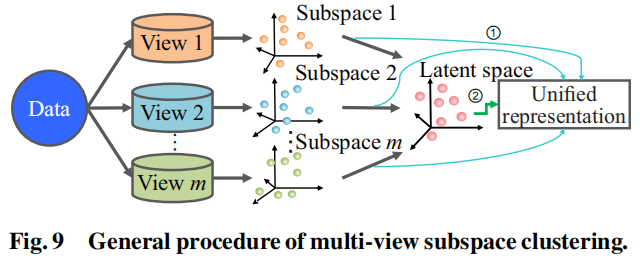
他获取统一特征表示的方法有两种

从多个子空间中直接学习统一表示
首先学习一个潜在的空间，然后得到这个统一的表示

最后这个统一的表示输入到一个线程的聚类模型中，以生成聚类结果。

Subspace learning-based MVC

基于学习的子空间MVC从多个低纬度的子空间中，寻找一种潜在空间，其假设数据点是从这个潜在子空间中绘制出来的。在本文中，基于子空间学习的MVC方法主要包括：子空间学习，子空间聚类，子空间映射，低秩拟合以及张量分解。

假设所有视图都是条件独立的，对于给定的聚类标签

基于典型相关分析(canonical correlation analysis)的多视图子空间学习方法：这个方法提供了高斯混合以及对数凹分布混合的辅助结果。
用于MVC的凸子空间表示学习方法：关键思想是检测一个跨多个视图的共享子空间表示，然后在共享的表示上使用标准的聚类算法。
用于多视图子空间聚类的协同训练框架：其在协同训练的模式下结合了经典的K-means和线性判别分析，利用在一个视图中自动学习到的标签去生成另一个视图的判别子空间。
基于子空间学习的特征加权方法：它根据视图的紧密性，自动地局部调整各组的特征权重。
多样新引导的多视图子空间聚类框架：其作者证明了利用特定的独立构造的矩阵对于MVC的实现是不够的，而探索其潜在的互补性是非常重要的。他们拓展现有的单视图子空间聚类到多视图领域，使用Hilbert Schmidt Independence Criterion作为以多样性的项，去探索多视图表示的多样性。
现有研究通常关注联合信息，而不是关注于促进每个视图的特征表示能力，为了解决这个问题，有人提出了一个具有极端学习的的框架，并在这个框架上实现了三个算法。
与第2和6个方法在公共视图上执行聚类不同，有人在所有视图上同时执行子空间聚类，其使用公共指标保证在不同视图中的聚类一致性。
有差别地嵌入K-means：其嵌入多个判别子空间的同步学习到多视图K-means聚类中，去形成一个统一的框架，这个框架自适应地控制这些子空间之间的相互协调。

为了有效地探索所有多视图中的数据相关一致性，用于多视图数据的使用相似度矩阵的子空间聚类方法被提出。其作者试图在所有的视图中找到一个关系或相似度一致性，作者被一个思想启发：对于每一个视图，相同子空间的数据对象有大的相似性，而不同子空间的数据对象有比较小的相似性。

也有人不用相似度矩阵，而是将低秩约束(global low-rank constraints)和本地交叉拓扑保持约束(local cross topology preserving constraints)引入到子空间聚类中，以表征数据相关性。也有一些其他方法结合了其他技术，比如稀疏子空间聚类，低秩近似以及张量分解。

上述的方法或框架的输出都只是一个单独的聚类，

有人提出了创新性的工作，其目的是找到基于子空间学习的替代性和多重聚类解决方案。其设计了一个MVC框架去找到所有的非冗余数据聚类视图，并使用这个框架提出了两个方法：正交聚类(orthogonal clustering)和在正交子空间上聚类(clustering in orthogonal subspace)。两者的区别在于，前者在聚类空间中寻找正交性，而后者是在特征空间中寻找的。
使用多个混合模型对数据进行多重概括：每一个混合模型在数据上通过使用一个在子空间映射上的Beta分布混合描述一个特定的视图。

在半监督聚类中，

用于半监督MVC的全新贝叶斯框架：其寻求检测多重和可替代的聚类。这个全新的框架用位于子空间映射中的多元混合分布处理多视图数据，以sample-level约束的形式处理先验知识，去表示哪一个对象是否应该被分到一组。
用于MVC的成对系数子空间表示模型：该模型利用先验知识，通过利用不同视图之间的关系去得到特定视图的稀疏表示。
约束的多视图视频人脸聚类方法：其同时考虑视频人脸对约束和多视图一致性。与现有的一些聚类仅在聚类阶段使用这些使用这些约束的聚类方法不同，该方法通过整个框架加强了成对约束，即稀疏子空间表示和谱聚类。

基于子空间学习的不完整MVC

统一子空间学习，特征选择和视图间和视图内的相似性到一个单一的目标函数中。其在不完整的多视图数据中学习一个潜在的表示，其中这个潜在的表示作为归一化指标矩阵的一个近似进行工作。
有人指出解决不完整视图的关键是去探索不同视图之间的连接性。这使得不完整数图能够在完整视图的帮助下被恢复，他们还利用通过这个子空间的其他观察视图来对不完整视图进行估计。

基于子空间学习研究用于不完整或者无标签的多视图数据的不完整多视图学习，在下图中展示了提出的子空间学习模型，其为不完整的多视图数据学习一个统一的潜在表示。

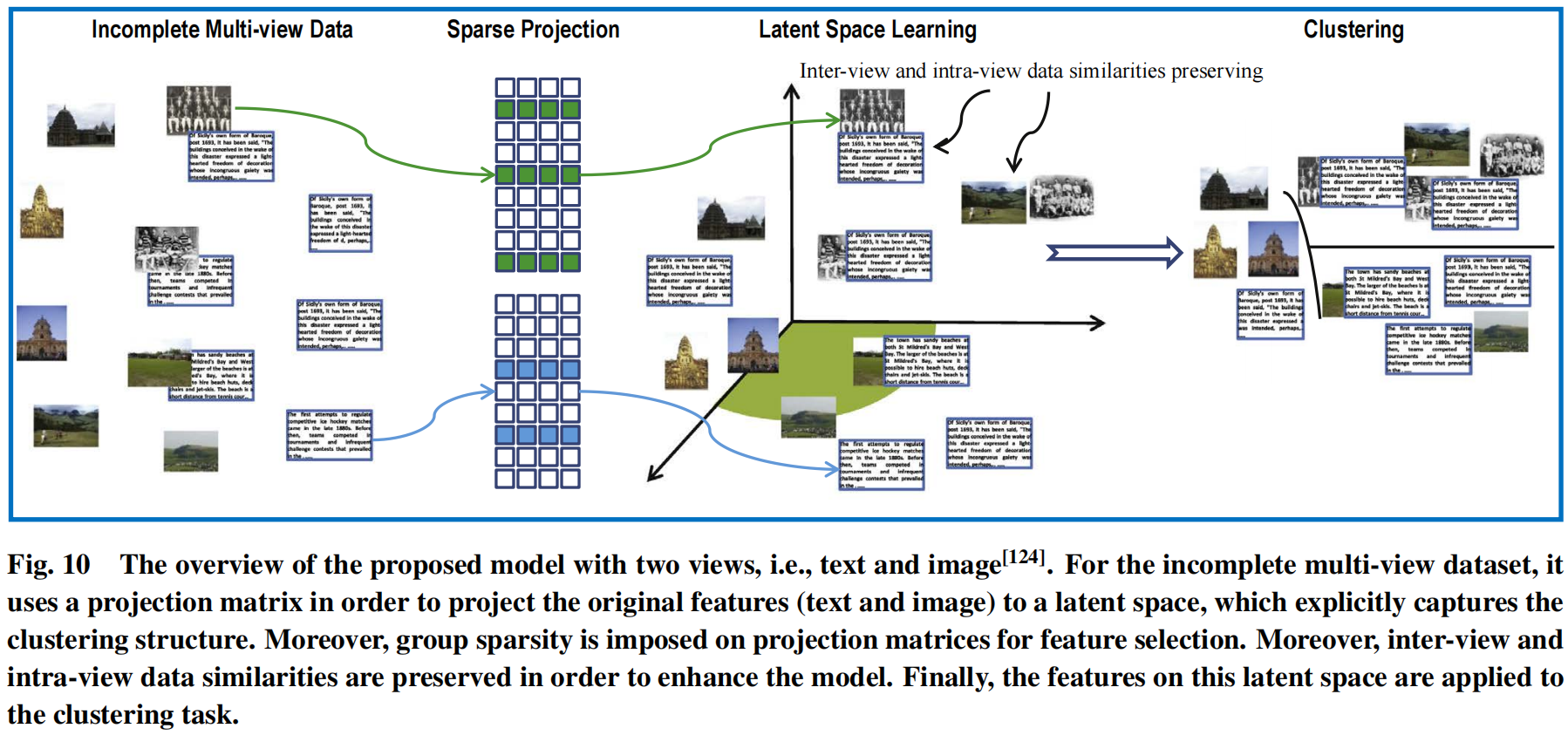
这个模型直接优化类别指标矩阵，其为不完整的特征集合建立一个桥梁。此外，还考虑使用特征选择去处理高纬和噪声特征。此外，视图间和视图内数据的结构被保存，并用于增强学习表现。最后，使用一个有效的优化算法提出了一个目标函数。

令 $X=\left[X_{c}^{v}, \hat{X}^{v}\right] \in \mathbb{R}^{d_{v} \times\left(n_{c}^{v}+\hat{n}^{v}\right)}$ 表示第v个视图的数据矩阵，其中 $X_{c}^{v} \in \mathbb{R}^{d_{v} \times n_{c}^{v}}$ ， $\hat{X} \in\mathbb{R}^{d_{v} \times \hat{n}^{v}}$ 分别表示在第v个视图上用于完整数据矩阵和部分实例数据矩阵。相似的， $Y=\left[Y_{c}^{v}, \hat{Y}^{v}\right] \in \mathbb{R}^{\left(n_{c}^{v}+\hat{n}^{v}\right) \times k}$ 表示第v个视图的类别指标，为了学习类别指标矩阵，其驱动一个映射矩阵 $U^{v} \in \mathbb{R}^{d_{v} \times k}$ ，并用于每一个视图，其目的是映射他们的原始空间到一个统一的空间中。目标函数可以用下面的公式表示:

$公式11： \begin{aligned} & \min _{U, Y} \underbrace{\sum_{i=1}^{m}\left\|\left[X_{c}^{v}, \hat{X}^{v}\right]^{\mathrm{T}} U^{i}-\left[Y_{c}^{v}, \hat{Y}^{v}\right]\right\|_{\mathrm{F}}^{2}}_{\text {Feature projection }}+\\ & \beta \underbrace{\sum_{i=1}^{m}\left\|U^{i}\right\|_{21}}_{\text {Feature learning }}+\gamma \underbrace{\sum_{p=1}^{m} \sum_{q=1}^{m} \operatorname{tr}\left(\left(U^{p}\right)^{\mathrm{T}} X^{i} L_{p q}(X)^{\mathrm{T}} U^{q}\right)}_{\text {Similarity preserving }}\\ & \text { s.t., } Y \in\{0,1\}^{n \times k}, \quad Y \mathbf{1}_{k}=\mathbf{1}_{n} \end{aligned}$

其中这里有三个项，使用投影矩阵取映射每一个不完整的视图来获得潜在空间，其用 $Y$ 表示；基于 $l_{21}-norm$ 正则化的用于每一个视图的特征选择；视图内核视图间数据相似度，通过使用拉普拉斯矩阵 $L_{pq}$ 来表示这个项。此外，对 $Y$ 事假的约束保证了每一个样本只属于一个组。

NMF-based MVC

NMF最初是作为一种降维技术研究，现已称为一种有效的潜在特征学习方法。非负约束使得基于部分的样本表示，从心里(psychological)和物理(physiological)上的证据来看，这与人类的认知过程是一致的。个点一个非负数据矩阵 $X\in\mathbb{R}^{d\times n}$ 作为输入， $X$ 的每一列都是一个样本的一个特征向量。NMF的目的是去发现两个非负矩阵 $W\in\mathbb{R}^{d\times p}$ 和 $H\in\mathbb{R}^{p\times n}$ ，他们的乘积可以充分地近似于原始矩阵。 $W$ 是一个作为偏置矩阵(基本空间)的项，而H表示置信度矩阵(表示特征)。 $p$ 表示所需的缩小尺寸，其中 $p \ll \min \{n, d\}$ 。重建过程可以看做是一个Frobenius norm优化问题，可以用下面的公式表示：

$公式12：\min _{W, H}\|X-W H\|_{\mathrm{F}}^{2}, \quad \text { s.t., } W \geqslant 0, H \geqslant 0$

常见的NMF方法有：G-arthogonal(G对角) NMF，正则化NMF，凸和半NFM(Convex and Semi-NMF)，多层NMF。

使用NMF的后期集成方法：其在每一个可用的视图上独立地生成聚类结果，构建这些聚类结果的中间矩阵表示，执行NMF在这些表示上，来协调由独立视图产生的组。
新型基于NMF的MVC框架：其直接地将数据输入到NMF，产生一个融合表示。
使用归一化策略的联合矩阵分解：其将每一个视图的表示推向公共一致性。
在每一个视图加权的基于NMF的半监督MVC算法：其发现了一个部分共享的潜在表示。通过这个学习来的多视图数据表示，引入了一个鲁棒的稀疏回归模型去预测聚类结果。
将数据点的相似度矩阵嵌入到NMF中，其本质上也是为MVC学习一个共享的潜在表示
将多视图NMF应用与服装图像聚类，通过采用一个新的正则化项，以保持每个视图的表示结果之间的结构不一致性。
使用补丁对齐策略的多视图NMF：该方法考虑到每个视图的局部集合结构，同时惩罚不同视图的差异。
使用平滑权重模式的新型自定义节奏学习算法：其不讲不同的视图或对象看做不同的位置，其集成了logistic函数的优点，并提供了概率权重。
用于大规模多视图数据的基于G-orthogonal NMF的鲁棒性多视图K-means聚类
用于图文网页新闻数据的多视图无监督方法：采用图像局部学习正则化正交NMF来学习伪标签，采用鲁棒的联合 $l_{2,1}-norm$ 来选择判别特征。
用于MVC的使用多层NMF的深度矩阵分解框架：其中使用半监督NMF在每一层学习多视图数据的分级表示。
使用 $l_{2,1}-norm$ 和分组 $l_1-norm$ 的多稀疏视图聚类方法
用于MVC的图(或流形)正则化的NMF：图正则化的NMF是NMF的一个拓展，已被证明可以提高基于流形假设的 $X$ 因子分解的质量，如果两个数据点在内部几何结构中接近，那么在新的偏置空间中，这两个数据点的偏置空间就会非常接近彼此。
基于图正则化的多视图NMF的聚类
通过部分标签信息构建的图嵌入框架：其考虑了稀疏约束
多流形正则NMF：线性地组合多个流形
基于SymNMF并用于MVC的图正则化对称NMF框架
通过概念分解的图正则化MVC方法

不完整的多视图聚类

合并加权NMF，以畜类每个不完整视图中缺失的对象，并将学习到的潜在表示特征推向一致性。
通过张量建模和因子分解得到的不完整数据的一般框架：首先使用核矩阵取生成跨所有视图的初始张量，然后给出一个具有稀疏约束的联合张量分解过程。这个过程的使用能够迭代地推进初始张量向潜在因子探索。
部分多视图聚类算法(PVC)：其实特地为两个视图数据集设计的方法。他采用NMF去学习一个潜在子空间，这个子空间中，属于同一组的样本彼此接近，来自相同视图的相似样本应该很好的分组。
通过考虑聚类相似性和流形保持约束条件来改进PVC
拓展PVC使其能够支持多视图和特定视图的图拉普拉斯正则化
根据视图内的约束（must-link和cannot-link约束），定义了每对视图之间的分歧，以指导因子分解过程

接下来详细介绍一下一种基于使用局部流形正则化的概念分解的自动加权的多视图概念聚类（MVCC）。MVCC的框架如下图所示：

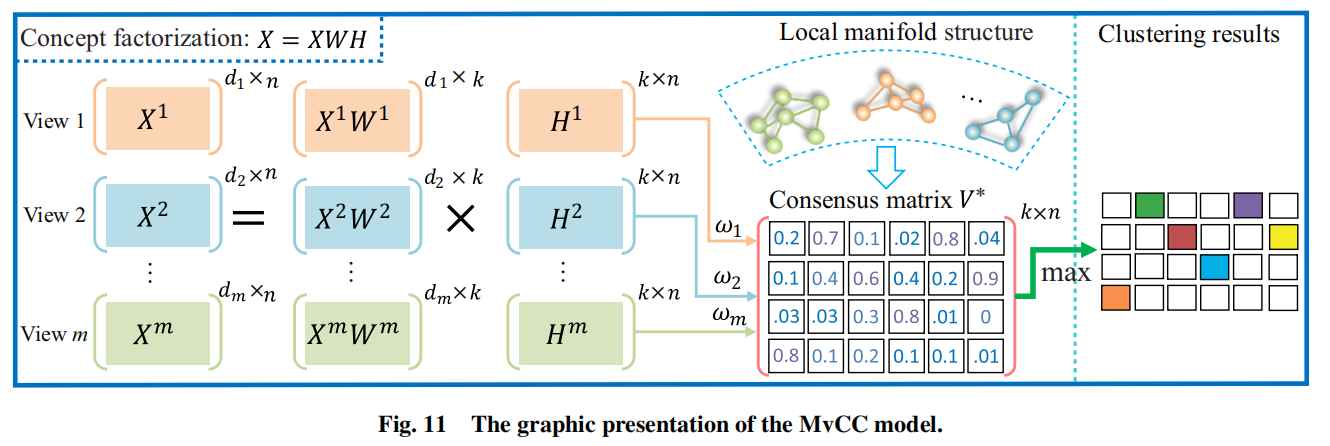
概念分解是NMF的一个变体，课用于处理包含负数的数据，同时运用在核空间上也是比较简单的。此外，局部流形正则化被纳入概念因子分解过程，以保持原始数据空间的局部集合结构。每个视图的权重都是自动确定的，提出的协同归一化机制使得融合在推动公共一致性表示方面有重要意义。此外，聚类结果从公共一致性表示中被直接驱动，不需要额外的聚类步骤。这是因为一致性矩阵是稀疏的。

给定多视图数据 $X=\left\{X^{1}, \ldots, X^{m}\right\}$ ，MVCC的目标函数可以用下面的公式表示：

$公式13：\begin{array}{c} \min _{H^{*}} \sum_{v=1}^{m}\left\{\begin{array}{l} \underbrace{\left\|X^{v}-X^{v} W^{v}\left(H^{v}\right)^{\mathrm{T}}\right\|_{\mathrm{F}}^{2}}_{\text {Concept factorization }}+ \\ \underbrace{\operatorname{tr}\left(\left(H^{v}\right)^{\mathrm{T}} L^{v} H^{v}\right)}_{\text {Local manifold regularization }} \\ \beta \underbrace{\omega_{v}\left\|H^{v}-H^{*}\right\|_{\mathrm{F}}^{2}}_{\text {Consensus representation }} \end{array}\right\}, \\ \text { s.t., } \quad W^{v} \geqslant 0, H^{v} \geqslant 0, \omega_{v} \geqslant 0, \sum_{v} \omega_{v}=1 \end{array}$

其中 $W^v$ 是联系矩阵， $H^v$ 是表示矩阵， $H^*$ 是一致性表示矩阵， $L^v$ 是拉普拉斯矩阵， $w^v$ 是第v个视图的权重， $\alpha$ 和 $\beta$ 是权衡参数(trade-off parameters)。权重 $w$ 是自动确定的， $\alpha$ 和 $\beta$ 使用的是经验值，然而，目标函数不能同时凸优化所有的变量。一种基于乘法更新规则的交替迭代算法被提出来优化参数。

Multi-task multi-view clustering

如前面所说，MVC在不同视图中探索一致性和互补性，以得到更好的聚类质量。另一个叫做多任务聚类(属于多任务学习领域)一起执行多个相关任务，使用这些任务之间的关系在单一视图数据中增强聚类表现。通过继承MVC和多任务聚类的属性，多任务多视图聚类(M²VC)使用一个或多个任务来处理每个单独的视图数据，如下图所示：

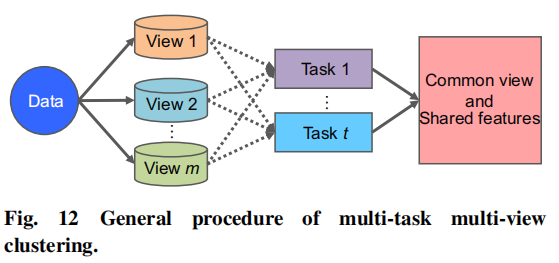
M²VC的主要挑战有：

找到一个方式去建模每一个视图中的任务内聚类
找到一个方式去探索多任务和多视图的关系，同时将任务间的知识相互传递

通过假设一个公共的底层子空间由多个相关的任务共享：

使用对每个视图进行一个任务处理的方式实现跨域多任务聚类：这个方法的目的是学习一个子空间，通过这个子空间，一个任务的知识可以传递到另一个任务上。作者还假设每个任务的特征向量的维数是相同的，每个任务上的聚类数也是相同的。
新的跨域多任务聚类放宽了第一个方法中的假设：其同时执行多个相关聚类任务，通过域自适应的方式。
基于三因子的NMF的多任务协同聚类方法：其目标函数由特定任务协同聚类和跨任务特征空间正则化构成
用于多视图数据的使用SymNMF的多任务聚类方法：其多个任务使用集合仿射变换同时执行，以控制任务内和任务间的知识共享。
通过使用一个多目标公式(可以看成是一个多任务问题)进行多视图谱聚类：这个多任务问题通过使用Pareto优化方式解决。
基于进化方法的多目标MVC集成方法
基于实例知识转移的多任务聚类算法：其学习了一个共享子空间，然后为每个独立的任务构建一个共享的最近邻相似度矩阵。其在每个任务的共享最近邻相似度矩阵上采用传统的谱聚类方法
利用多视图之间的相关信息，将谱聚类和判别分析纳入一个统一的框架中：谱聚类的目的是挖掘聚类结构，判别分析的目的是保护这个结构。
集成了视图内任务聚类、多视图关系学习和多任务关系学习，提出了两种M²VC算法：基于二分图的M²VC算法和基于半NMF的M²VC算法。

还有一些不属于上述5类的方法：

1. 基于马尔科夫随机场的多模态聚类
1. 基于多视图谱聚类的多视图集成聚类
1. 使用集成技术的多核K-means聚类
1. 基于K-means的双级加权MVC
1. 多视图模糊聚类

在多任务多视图中，任务通过视图进行关联，M²VC的关键步骤是连接公共视图上的特征，以便于聚合相关的任务。接下来将详细介绍一种基于协同聚类的典型M²VC框架，其结构如下图所示：

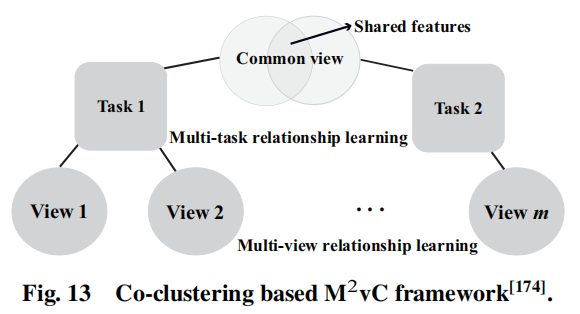
其中，正方形区域表示数据样本集，圆形区域表示在一个视图下的每一个任务中的数据特征集合。值得注意的是任务1和任务2的样本有一个公共视图，其中包含共享任务特征(浅灰色重叠区域)和任务特定特征(浅灰色非重叠部分)。这个框架由三个组件构成：视图内任务聚类，多视图关系学习，多任务关系学习。在这个框架下，提出了两种M²VC算法，一个是基于二分图的M²VC算法，只能处理非负值的数据。另一个是基于半非负矩阵因子分解的M²VC算法，其能够解决数据同时含有负值和非负值的情况。

给定T个聚类任务，每个任务覆盖 $m_t$ 个视图， $S$ 是公共视图的索引集合， $T_v$ 是公共视图下所有任务的索引集合。

对于视图内任务聚类，对每个任务的每个视图中的数据对象进行协同聚类，完成整个算法那的基本部分，确保每个任务的每个视图局部可用只是的保存，以避免消极转移。对于多视图关系学习，其最小化每个任务中每对视图下的数据聚类之间的差异。对于多任务关系学习，其使用协同聚类，假设相关任务应该共享一些共同的或相关的特征，在每个公共视图下的相关任务之前驱动一个共享的子空间。

M²VC聚类框架可以用下面的公式表示：

$公式14：\min \sum_{t=1}^{T}\left(\sum_{i=1}^{m_{t}} H_{1}+\lambda \sum_{i=1}^{m_{t}} \sum_{j \neq i}^{m_{t}} H_{2}\right)+\mu \sum_{i \in S} \sum_{t \in T_{i}} H_{3}$

其中 $\sum_{i=1}^{m_{t}} H_{1}$ 是将每个任务t中所有视图的数据对象和特征进行协同聚类。 $\sum_{i=1}^{m_{t}} \sum_{j \neq i}^{m_{t}} H_{2}$ 是最小化在每一任务t中任意两个不同视图聚类分布之间的差异。 $\sum_{i \in S} \sum_{t \in T_{i}} H_{3}$ 是通过与第一个组件相同的协同聚类方法得到每一个公共视图的共享子空间。 $\lambda$ 和 $\mu$ 是权衡参数。

Publically Available Datasets

3Sources Dataset：http://mlg.ucd.ie/datasets/bbc.html

以多视图文本语料库，从三个在线新闻服务商的新闻文章进行构建。这个仓库也有多视图推特数据集，其是一个用于社交网络发掘的推特数据集。还有BBC和BBCSport数据集，两个都是来自BBC新闻的合成文本数据集。
WebKb Datasets：http://www.cs.cmu.edu/afs/cs.cmu.edu/project/theo-20/www/data

这个数据集包含来自四个不同大学的计算机科学部门的网页数据，明明为four multi-view datasets
Newsgroup Datasets：http://lig-membres.imag.fr/grimal/data.html

其是使用3种不同的预处理方式处理NG20数据集产生的子数据集。这个仓库也有：Reuters，Multilingual Dataset, Cora Dataset, CiteSeer Dataset, Movies617 Dataset, 以及 mini WekbDatasets。
Wikipedia Article Dataset：http://www.svcl.ucsd.edu/projects/crossmodal/

其是维基百科的特色文章精选部分，他们有完整版本或小版本
Handwritten Digit Dataset：http://archive.ics.uci.edu/ml/datasets/Multiple+Features

由来自UCI仓库的手写数字(0-9)的特性部分组成
100leaves Dataset：https://archive.ics.uci.edu/ml/datasets/One-hundred+plant+species+leaves+data+set

其包括植物叶子的16个不同类型，其中每一个类型有100个样本。对于每一个样本，给出了形状描述符，细尺度边缘和文理直方图。
Corel Images Dataset：https://archive.ics.uci.edu/ml/datasets/Corel+Image+Features

这个数据集从Corel图像集合的精选图像中提取，他提供了4组特征，分别叫做：颜色直方图，颜色直方图布局，颜色矩(color moments)以及共现纹理(co-occurence texture)
YouTube Video Dataset：https://archive.ics.uci.edu/ml/datasets/YouTube+Multiview+Video+Games+Dataset

这个数据大约有 $1.2\times 10^5$ 个实例，其中每个实例由13种特征描述，并且也有它自己的类别信息。

Conclusion and Discussuion

简单来说，协同训练类型的算法可以交互式地交换信息，增强不同视图的聚类结果。但当视图变成3个以上时就会变得棘手；基于核的MVC继承了核的有点，而带来了比较高的计算复杂度；多视图图聚类引入了谱图理论，同时依赖结构亲和度(或相似度)矩阵；多视图子空间聚类方法有直接的可解释性，也有初始化依赖性；多任务多视图集成了多任务聚类和多视图聚类的属性，然而，这个类型仍然处于婴儿期。

接下来介绍MVC领域的挑战

视图的正确性：找到一种了解一个视图是否正确的方法，对MVC来说至关重要。由于MVC探索所有可用的视图来提高聚类效果，因此不正确的视图是非常有害的。尽管这些工作利用权重对这些视图进行利用，但错误可能从误导的视图传播到其他视图，因此，必须在很大程度上解决或环节这个问题，以确保MVC的有效性。
融合的合适时机：现有的MVC在聚类过程中对多视图数据采用三种融合策略：数据融合，映射特征融合，结果融合。目前MVC的研究工作大多集中在第二种融合策略上，然而，目前并没有理论基础来决定哪一个是最好的。为了解释他们的本质，需要进行理论和方法上的研究。
不完整的MVC：尽管人们已经对不完整的多视图数据进行了一些尝试，正如我们在该类别的每个部分中提到的那样，不完整的MVC仍然是一个具有挑战性的问题，在现实生活中，数据丢失经常发生，而对不完整MVC的研究却没有被广泛研究。预计将会努力对不完整的MVC进行研究。
多任务多视图聚类：这个方向是MVC研究的新趋势，然而，这一趋势伴随着一些挑战，如找到一种方法来探索不同任务和不同视图之间的联系，找到一种在不同视图之间传递知识的方法。