「论文阅读(简)」Reverse Graph Learning for Graph Neural Network

论文名称：Reverse Graph Learning for Graph Neural Network

作者：Liang Peng; Rongyao Hu; Fei Kong; Jiangzhang Gan; Yujie Mo; Xiaoshuang Shi; Xiaofeng Zhu

时间：2022-4

期刊：IEEE Transactions on Neural Networks and Learning Systems

原文摘要

Graph neural networks (GNNs) conduct feature learning by taking into account the local structure preservation of the data to produce discriminative features, but need to address the following issues, i.e., 1) the initial graph containing faulty and missing edges often affect feature learning and 2) most GNN methods suffer from the issue of out-of-example since their training processes do not directly generate a prediction model to predict unseen data points. In this work, we propose a reverse GNN model to learn the graph from the intrinsic space of the original data points as well as to investigate a new out-of-sample extension method. As a result, the proposed method can output a high-quality graph to improve the quality of feature learning, while the new method of out-of-sample extension makes our reverse GNN method available for conducting supervised learning and semi-supervised learning. Experimental results on real-world datasets show that our method outputs competitive classifification performance, compared to state-of-the-art methods, in terms of semi-supervised node classifification, out-of-sample extension, random edge attack, link prediction, and image retrieval.

研究问题

图神经网络通过考虑数据的局部结构去产生有区别的特征，从而实现特征学习。但这个领域仍然存在两个问题

1. 如果初始图包含存在缺陷或者缺失边，这个初始图通常会影响特征的学习。
2. 包含有噪声和异常值的原始数据很容易导致两个数据节点的不正确关系
3. 大部分的GNN方法不能解决out-of-example(外部数据)的问题，因为训练过程中，他们不是直接生成一个预测模型去预测不可见的数据点。

算法任务与应用：

1. 有监督节点分类
2. 通过使用外部数据拓展的有监督节点分类
3. 随机边缘攻击（随机去除图的一些边）
4. 连接预测（遮掩一部分边，看模型是能重新找回边）
5. 图像检索

理论基础：

1. 图神经网络能够捕获数据节点之间的局部集合结构，从非欧几里得数据中提取局部的，成分的以及判别的特征。
2. 图神经网络的输入通常是原始数据和一个包含局部结构的初始图(数据点和他的邻居之间的相似性)。
3. 图的底层信息对图神经网络模型至关重要，错误的信息（如不正确的边）和不足的信息（如缺失的边）将会传递给网络构建，误导模型，限制其有效性
4. 低质量的图不能产生判别信息

创新点：

1. 反转图学习：原始数据的表征通常含有噪声和荣誉，因此，在原始数据上构建的初始图结构是不可靠的，低质量的。为了解决这一问题，提出了翻转图学习，这个图是从原始数据的本质空间(intrinsic space)构建的。因此噪声问题会被缓解。反转图学习也可以根据特征学习的更新自适应地调整。
2. 外部样本拓展：将每个不可见数据点的特征分配为其最近邻节点的特征。本文的方法在反转图学习层中，从原始数据的本质空间得到初始图，以保证获得真正接近的节点。

提出方法：

问题定义（节点分类为例）

为了执行传递特征表示，同时考虑数据节点之间的数据对关系，GNN模型通常会有几个隐藏层，每一层包括特征学习和邻接节点聚合。GNN的第l+1层的图卷积操作，可以用下面的公式表示：

$$公式1：\mathbf{H}^{l+1}=\sigma(\mathbf{D}^{-\frac 12}\mathbf{A}\mathbf{D}^{-\frac{1}{2}}\mathbf{H}^l\mathbf{W}^l)$$

其中$\mathbf{D} \in \mathbf{R}^{n \times n}$是初始图$\mathbf{A} \in \mathbb{R}^{n \times n}$的拉普拉斯矩阵，$\mathbf{W}^{l} \in \mathbb{R}^{d_{l} \times d_{l+1}}$是第l层的权重参数($d_l$和$d_{l+1}$分别表示维度)。$\sigma(.)$是激活函数。从GNN的最后一层得到的嵌入特征$Z$，在模型最后的预测层，可以用下面的公式表示

$$公式2：\mathbf{O}=\operatorname{Softmax}(\text { Linear }(\mathbf{Z}))$$

其中$Linear(\cdot)$用于每一个类别可能性的回归预测。$\mathbf{O} \in \mathbb{R}^{n \times c}$表示GCN模型的输出，其中$c$是类别的数量。用交叉熵损失函数来衡量分类的效果

$$公式3：\mathcal{L}_{\mathrm{GNN}}=-\sum_{\mathrm{v}_{i} \in Y_{L}}\left(y_{i} \log \left(o_{i}\right)+\left(1-y_{i}\right) \log \left(1-o_{i}\right)\right)$$

其中$Y_L$是标记节点集合，$y_i$是ground truth，$o_i$是对应的预测结果。为了克服初始图中的多种缺点(比如噪声边)，GLCN提出了一个自适应的GNN方法去自适应更新图，并学习特征：

$$公式4：\mathcal{L}=\mathcal{L}_{\mathrm{GNN}}+\gamma \mathcal{L}_{\mathrm{GL}}$$

其中$\gamma$是一个超参数，$\mathcal{L}_{\mathrm{GL}}$用下面的公式表示：

$$公式5：\begin{aligned} \mathcal{L}_{\mathrm{GL}}: & \min _{\mathbf{S}} \sum_{i, j=1}^{n}\left\|\mathbf{x}_{i}-\mathbf{x}_{j}\right\|_{2}^{2} s_{i j}+\|\mathbf{S}\|_{F}^{2} \\ \text { s.t., } & \sum_{j=1}^{n} s_{i j}=1, \quad s_{i j}>0, i, j=1, \ldots, n \end{aligned}$$

其中$s_{ij}$是$\mathbf{x}_i$和$\mathbf{x}_j$之间的欧氏距离下学习到的潜在图结构。

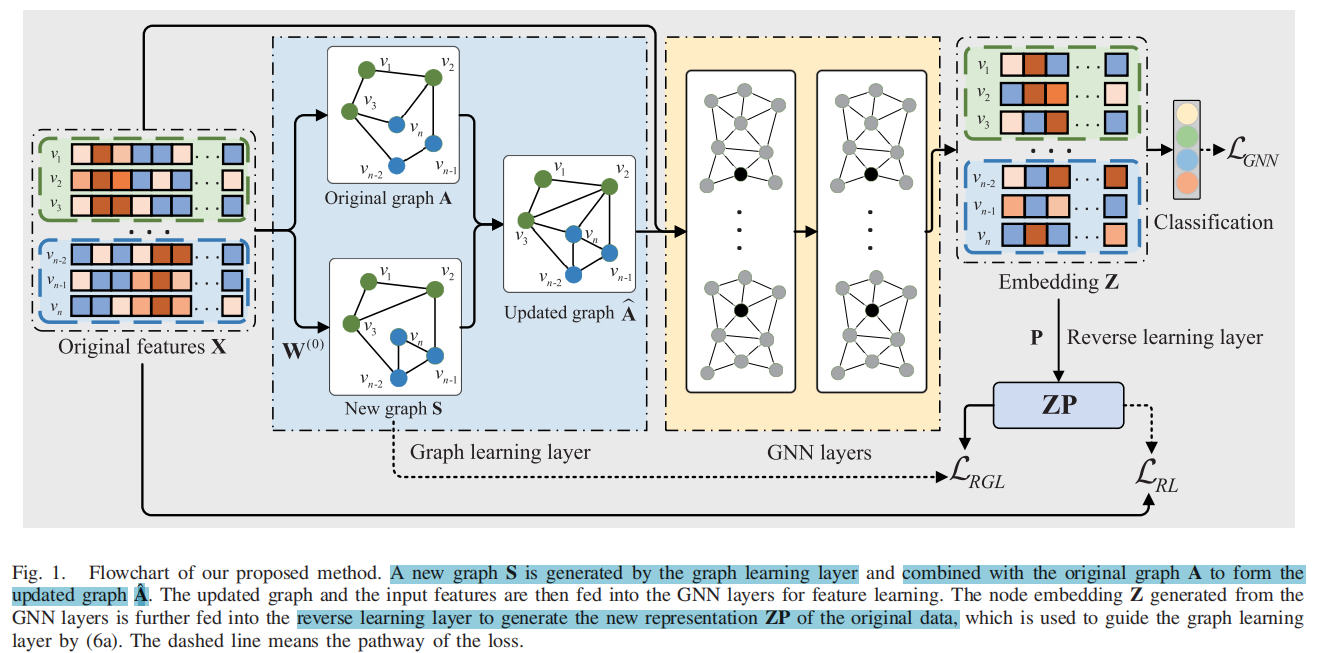
提出模型结构图：

反转图学习(对应图中含有ZP的一列)

$\mathbf{X}=\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{n}\right\} \in \mathbb{R}^{n \times D}$表示输入空间$\mathcal{X}$的节点特征矩阵，其中第i个节点$v_i$有D-dimensional的表示，并将这个表示定义为$\mathbf{z}_{i} \in \mathbb{R}^{1 \times d}$。本文进一步提出反转图嵌入通过满足语义一致性和结构一致性去保护数据在本质空间的局部结构。

语义一致性保护原始语义信息，结构一致性保护数据点在输入空间$\mathcal{X}$的局部结构。翻转图嵌入$\mathbf{z}_{i} \mathbf{P}$和$\mathbf{z}_{j} \mathbf{P}$应该保护第i个节点$v_i$和第j个节点$v_j$之间的相似性。本文假设，存在一个本质空间，使得$X$的新表示通过变换矩阵$\mathbf{P}$用$\mathbf{ZP}$表示。

在这个反转图学习中，公式5中的被改写为：

$$公式6：\left\{\begin{aligned} \mathcal{L}_{\mathrm{RGL}}: & \min _{\mathbf{S}} \sum_{i j}^{n}\left\|\mathbf{z}_{i} \mathbf{P}-\mathbf{z}_{j} \mathbf{P}\right\|_{2}^{2} s_{i j}+\|\mathbf{S}\|_{F}^{2} \\ & \text { s.t., } \sum_{j=1}^{n} s_{i j}=1, \quad s_{i j}>0, i, j=1, \ldots, n \\ \mathcal{L}_{\mathrm{RL}}: & \min _{\mathbf{P}, \mathbf{P}^{T} \mathbf{P}=\mathbf{I}}\|\mathbf{X}-\mathbf{Z P}\|_{F}^{2} \end{aligned}\right.$$

其中$P^T$是矩阵$P$的转置，$I$是一个单位矩阵。$\mathcal{L}_{RGL}$通过引导图学习过程得到结构一致性。$s_{ij}$是$\mathbf{z}_i$和$\mathbf{z}_j$之间的欧氏距离下学习到的潜在图结构（$Z$表示在嵌入空间中）。$v_i$和$v_j$之间的距离$\left\|\mathbf{z}_{i} \mathbf{P}-\mathbf{z}_{j} \mathbf{P}\right\|_{2}^{2}$越大，会使得$s_{ij}$更小。

$\mathcal{L}_{RL}$通过训练从$\mathbf{X}$到$\mathbf{Z}$得反转映射到语义一致性。$\|\mathbf{X}-\mathbf{Z P}\|$与自编码器的方法相似，因为他学习$X$的新表示$ZP$。同时可以促进$ZP$关注抽象潜在因子(本质属性)。

本文的方法从GNN中得到的新表征$Z$，然后固定反转图的映射函数$P$，通过ZP展开的本质空间中学习反转图。

用于新图的相似度指标学习

在本问题出的GNN模型的第一层中，目的是优化表示两个数据点之间新表示的成对关系的新图S。使用余弦距离去定义新图S边的权重

$$公式7：s_{i j}=\cos \left(\mathbf{x}_{i} \mathbf{W}^{(0)}, \mathbf{x}_{j} \mathbf{W}^{(0)}\right)$$

其中$s_{i j}$是数据点$v_i$和数据点$v_j$的边权。$s_{i j} \in[0,1]$。$\mathbf{W}^{(0)} \in \mathbf{R}^{D \times d^{\prime}}\left(d^{\prime} \leq D\right)$是权重矩阵。通过保持每个节点的前k个相邻节点的相似度(边权)，并将其他节点设置为0，从而获得一个稀疏图S。然后在对S进行归一化，使其满足$\sum_{j=1}^{n} s_{i j}=1, s_{i j}>0$。

在更新S的过程中，也要利用初始图A去保证S的更新能寻回缺失的边，S的更新公式可以使用下面的方式表示：

$$公式8：\hat{\mathbf{A}}=(1-\eta) \mathbf{A}+\eta \mathbf{S}$$

其中$\eta$是权衡$\mathbf{S}$和$\mathbf{A}$的超参数，A中缺失的边可以通过反转图S找回，因此把$\hat{A}$输入到GNN中比直接输入初始图A有更高的质量。

目标函数

GNNlayer(图中图神经网络的部分)可以用下面的公式表示：

$$公式9：\mathbf{Z}=\sigma\left(\hat{\mathbf{A}} \sigma\left(\hat{\mathbf{A}} \mathbf{X} \mathbf{W}^{(1)}\right) \mathbf{W}^{(2)}\right)$$

$\mathbf{W}^{(1)}$和$\mathbf{W}^{(2)}$是这两层GNN的权重参数。

目标函数可以用下面的公式表示：

$$公式10：\mathcal{L}=\mathcal{L}_{\mathrm{GNN}}+\beta \mathcal{L}_{\mathrm{RGL}}+\gamma \mathcal{L}_{\mathrm{RL}}$$

$\beta$和$\gamma$是两个权衡公式10中损失的超参数。损失的更新顺序是：$\mathcal{L}_{\mathrm{GNN}} \Rightarrow \mathcal{L}_{\mathrm{RGL}} \Rightarrow \mathcal{L}_{\mathrm{RL}}$

先固定GNN的参数$\mathbf{W}^{(1)}$和$\mathbf{W}^{(2)}$，然后优化图学习层的参数$\mathbf{P}$。

然后固定参数$\mathbf{P}$，优化反转图的参数$\mathbf{W}^{(0)}$和GNN的参数$\mathbf{W}^{(1)}$和$\mathbf{W}^{(2)}$。

外部数据样本拓展

查询扩展(QE)将不可见数据点的特征分配为其K个最近邻的加权平均值，来解决外部数据样本的问题。但是这个方法受限于从高维原始数据中构建的最近邻节点的质量。

本文通过图学习层，提出优化最近邻节点的选择，具体来说，在整个网络训练完成后，可以得到图学习层的$\mathbf{W}^{(0)}$，GNN层的$\mathbf{W}^{(1)}$和$\mathbf{W}^{(2)}$以及用于反转图学习的$\mathbf{P}$。对给定的不确定数据点(外部样本数据点)$\mathbf{x}_q$，使用$\mathbf{W}^{(0)}$将其投影到低纬的本质空间中，其中连个数据节点之间的聚类是有区别的。$\mathbf{x}_q$和训练数据$\mathbf{X}_{train}$可以被计算为：

$$公式11：\mathbf{S}_{q}=\cos \left(\mathbf{x}_{q} \mathbf{W}^{(0)}, \mathbf{X}_{\text {train }} \mathbf{W}^{(0)}\right)$$

然后通过下面的公式选择其邻居

$$公式12：\mathcal{N}_{q} \leftarrow \operatorname{topk}\left(\mathbf{S}_{q}\right)$$

在一个隐藏层中，不确定数据节点的表示是k个最近邻的邻居的加权平均值和其在前一层的表示$\mathbf{f}^{(l)}_p$的总和。最后使用softmax函数去预测不可见节点的标签。

$$公式13：\mathbf{H}_{q}^{(l)}=\sigma\left(\mathbf{W}^{(l)}\left(\sum_{\mathbf{x}_{p} \in \mathcal{N}_{q}} \mathbf{s}_{q p} \mathbf{f}_{p}^{(l)}+\mathbf{H}_{q}^{(l-1)}\right)\right)$$

本文的方法解决外部数据样本的主要思想是从数据点的本质空间中发现不可见数据点的邻居，并使用高质量的自适应地更新。本文也通过在训练过程中生成一个易于理解的映射函数去预测不可见数据点，本文的方法从公式6中的新表示学习潜在图结构。

实验方式：

对5个任务（节点有监督分类，使用外部数据拓展的有监督学习节点分类，随机边缘攻击，连接预测，图像检索）上使用11个公开数据集与现有12个方法进行对比实验，主要指标是分类的准确率(accuracy)。

在消融实验中

1. 反转图学习的有效性：使用反转图学习与QE方法结合提出了一种新的方法，用于解决外部样本问题，结果是比原本的QE效果要好。
2. 参数敏感度分析：
   1. 在之前提到的生成新图S的过程中，设置的最近邻超参数k，对于这个模型的效果是敏感的
   2. 对使用初始图A和新图S进行更新时的超参数$\eta$进行变化，发现新图S对GNN模型有重要的影响
   3. 损失函数中的$\beta$和$\gamma$参数是不敏感的。