论文名称：Multi-VAE: Learning Disentangled View-common and View-peculiar Visual Representations for Multi-view Clustering

作者：Jie Xu; Yazhou Ren; Huayi Tang; Xiaorong Pu; Xiaofeng Zhu; Ming Zeng; Lifang He

年份：2021-10

期刊或会议：2021 IEEE/CVF International Conference on Computer Vision (ICCV)

代码：https://github.com/SubmissionsIn/Multi-VAE

原文摘要

Multi-view clustering, a long-standing and important research problem, focuses on mining complementary information from diverse views. However, existing works often fuse multiple views’ representations or handle clustering in a common feature space, which may result in their entanglement especially for visual representations. To address this issue, we present a novel VAE-based multi-view clustering framework (Multi-VAE) by learning disentangled visual representations. Concretely, we define a view-common variable and multiple view-peculiar variables in the generative model. The prior of view-common variable obeys approximately discrete Gumbel Softmax distribution, which is introduced to extract the common cluster factor of multiple views. Meanwhile, the prior of view-peculiar variable follows continuous Gaussian distribution, which is used to represent each view’s peculiar visual factors. By controlling the mutual information capacity to disentangle the view common and view-peculiar representations, continuous visual information of multiple views can be separated so that their common discrete cluster information can be effectively mined. Experimental results demonstrate that Multi-VAE enjoys the disentangled and explainable visual representations, while obtaining superior clustering performance compared with state-of-the-art methods.

任务与存在问题

多视图聚类关注于从多个视图中挖掘互补信息，但现有的工作仍然存在一些问题：

  1. 现有的工作大豆融合多视图特征和在一个公共特征空间中处理聚类，这些都有可能使得不同视图的不同视觉表示缠绕在一起。
  2. 现有多视图聚类的方法核心瓶颈是其高复杂性，这使得处理大规模数据聚类任务不现实。

主要工作

提出一个通过学习离散视觉特征的新颖的基于VAE（变分自编码器）的多视图聚类框架（Multi-VAE）。在生成模型中定义视同公用变量和视图特定变量。其中视图公用变量的先验近似准许Gumbel Softmax分布，用于提取多视图中的公共聚类因子。同时视图特定变量的先验服从高斯分布，用于表示每个视图的特定视觉因子。通过控制交互信息的容量去离散化视图公共表示和视图特定表示，使得连续的多视图视觉信息被分离，以便于有效地挖掘他们共同的离散信息。

理论基础

  1. 聚类的目的是使用相似模式或特征将数据项分配到相同的组中。
  2. 深度学习的聚类方法客服了浅层模型的缺点，在集群性能上取得了相当大的进展。
  3. 多视图聚类可以得到更加包含在多视图数据中更加复杂的特征。
  4. 聚类信息是离散的，其是所有视图的最大公共视觉信息的一个抽象
  5. 每个视图的特有视觉信息是连续的，他们都对聚类有不同的影响

创新点

  1. 提出了一个称为Multi-view的新颖的多视图VAE框架，其引入视图公共变量和视图的特有变量，去挖掘离散的聚类因子和连续的视觉因子。
  2. 在这个模型中分离了所有视图的公共聚类表示和每个视图的特定视觉表示。通过这个方式在挖掘他们用于聚类的互补信息时减弱了多视图多余信息的干扰。
  3. Multi-VAE与其他忙伐相比，具有明显的聚类性能，此外他的复杂度与数据大小呈线性增长。这是第一次尝试通过学习离散表征和解释表征实现MVC。

提出的方法

模型结构图

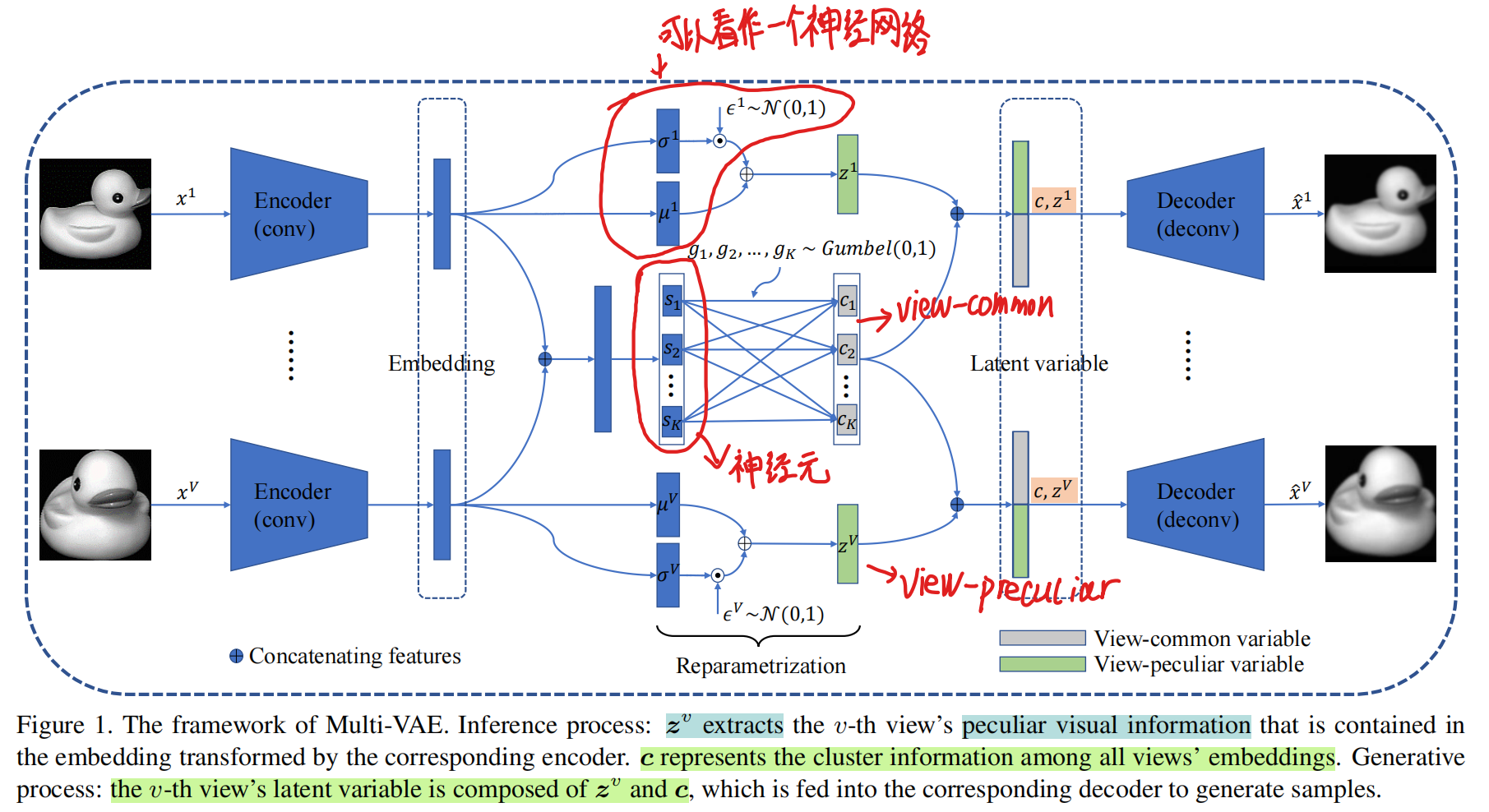
image-20220803173820287

结构

给定多视图图像数据集{xi1,xi2,...,xiV}i=1N\{\mathbf{x}_i^1,\mathbf{x}_i^2,...,\mathbf{x}_i^V\}_{i=1}^N，每个样本有V个含有不同视觉信息的视图，N为数据的大小。多视图聚类的目标是将这些数据分成K个簇。

因为本文的动机是通过VAE学习多个视图的离散表示，在这里引入了独立的视图公共变量c∈RK\mathbf{c}\in\mathbb{R}^K，视图特定变量{z∈RZv}v=1V\{\mathbf{z}\in\mathbb{R}^{Z_v}\}_{v=1}^V去建模多视图数据。通过联合概率得到生成的模型：

公式1：p(xv,zv,c)=p(xv∣zv,c)p(zv,c)=p(xv∣zv,c)p(zv)p(c),公式1：\begin{aligned} p\left(\boldsymbol{x}^{v}, \boldsymbol{z}^{v}, \boldsymbol{c}\right) &=p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right) p\left(\boldsymbol{z}^{v}, \boldsymbol{c}\right) \\ &=p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right) p\left(\boldsymbol{z}^{v}\right) p(\boldsymbol{c}), \end{aligned}

其中视图公共变量c\mathbf{c}被所有视图共享，并表示他们的聚类信息。对于第v个视图，视图特定变量zv\mathbf{z}^v表示特定的数据信息（角度，大小，风格等）。让{xv}\left\{\boldsymbol{x}^{v}\right\}表示所有视图数据{x1,x2,…,xV}\left\{\boldsymbol{x}^{1}, \boldsymbol{x}^{2}, \ldots, \boldsymbol{x}^{V}\right\}，那么，c\mathbf{c}和zv\mathbf{z}^v的后验概率(posterior)可以分别用p(c∣{xv})p\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)和p(zv∣xv)p\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)表示。考虑到在VAE中计算完整的后验概率是苦难的，所以使用qϕ(c∣{xv})q_{\phi}\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)和qϕv(zv∣xv)q_{\phi^{v}}\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)进行参数化，通过ϕ\phi和ϕv\phi^v去近似后验概率。

推理过程

在推理过程中，将所有的嵌入特征拼接在一起以学习他们的公共特征（图中Embeding右边加号的位置）。设置K个神经元s={s1,s2,…,sK}s=\left\{s_{1}, s_{2}, \ldots, s_{K}\right\}(图中的ss部分)得到视图公共语义变量c\boldsymbol{c}。其中c\mathbf{c}是一个one-hot编码表示。由于离散随机变量对神经网络的参数是不可微的，所以将视图公共变量的先验设置为独立聚云Gumbel Softmax分布的乘积，即p(c)=p(c1)p(c2)…p(cK)p(\boldsymbol{c})=p\left(c_{1}\right) p\left(c_{2}\right) \ldots p\left(c_{K}\right)，其中p(ck)∼Gumbel(0,1)p\left(c_{k}\right) \sim Gumbel(0,1)。因此，近似的后验概率qϕ(c∣{xv})q_{\phi}\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)可以表示为：

公式2：qϕ(c∣{xv})=∏k=1Kqϕ(ck∣{xv}).公式2：q_{\phi}\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)=\prod_{k=1}^{K} q_{\phi}\left(c_{k} \mid\left\{\boldsymbol{x}^{v}\right\}\right) .

根据Gumbel-Max重构参数技巧，公式2可以进一步表示为

公式3：qϕ(ck∣{xv})=G(s)=exp⁡((log⁡sk+gk)/τ)∑i=1Kexp⁡((log⁡si+gi)/τ)公式3：q_{\phi}\left(c_{k} \mid\left\{\boldsymbol{x}^{v}\right\}\right)=\mathcal{G}(\boldsymbol{s})=\frac{\exp \left(\left(\log s_{k}+g_{k}\right) / \tau\right)}{\sum_{i=1}^{K} \exp \left(\left(\log s_{i}+g_{i}\right) / \tau\right)}

其中gk∼Gumbel⁡(0,1)g_{k} \sim \operatorname{Gumbel}(0,1)和τ\tau是活性参数，用于控制松弛。假设其他视觉信息是连续的，视图特特定变量的先验概率是标准正态分布p(zv)∼N(0,I)p\left(\boldsymbol{z}^{v}\right) \sim \mathcal{N}(\mathbf{0}, \mathbf{I})，后验概率qϕv(zv∣xv)q_{\phi^{v}}\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)可以被分解的高斯分布参数化为：

公式4：qϕv(zv∣xv)=∏i=1Zvqϕv(ziv∣xv).公式4：q_{\phi^{v}}\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)=\prod_{i=1}^{Z_{v}} q_{\phi^{v}}\left(z_{i}^{v} \mid \boldsymbol{x}^{v}\right) .

根据重构参数技巧，公式4可以等价于下面的式子

公式5：qϕv(ziv∣xv)=N(μiv,(σiv)2)=μiv+σivϵiv,公式5：q_{\phi^{v}}\left(z_{i}^{v} \mid \boldsymbol{x}^{v}\right)=\mathcal{N}\left(\mu_{i}^{v},\left(\sigma_{i}^{v}\right)^{2}\right)=\mu_{i}^{v}+\sigma_{i}^{v} \epsilon_{i}^{v},

其中ϵiv∼N(0,1)\epsilon_{i}^{v} \sim \mathcal{N}(0,1)，μiv\mu_{i}^{v}和σiv\sigma_{i}^{v}通过以第v个视图的嵌入特征为输入的神经网络进行参数化。

生成过程

每个视图的潜在变量包含视图公共变量c\mathbf{c}和视图特定变量zv\mathbf{z}^v。第v个视图的解码器输出（可能性）可以表示为：

公式6：x^v=pθv(xv∣zv,c)公式6：\hat{\boldsymbol{x}}^{v}=p_{\theta^{v}}\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)

在这个结构中，参数ϕ,{ϕ1,ϕ2,…,ϕV}\phi,\left\{\phi^{1}, \phi^{2}, \ldots, \phi^{V}\right\}和ϕ,{ϕ1,ϕ2,…,ϕV}\phi,\left\{\phi^{1}, \phi^{2}, \ldots, \phi^{V}\right\}是部分共享的。

变分下界

变分推理的目标是最大化观察到的多视图数据的可能性函数，通过Jensen不等式，模型的log可能性可以用下面的公式表示：

公式7：∑v=1Vlog⁡p(xv)=∑v=1Vlog⁡∫zv∑cp(xv,zv,c)dzv≥∑v=1VEq(zv,c∣{xv})[log⁡p(xv,zv,c)q(zv,c∣{xv})]=∑v=1VLELBO(xv)公式7：\begin{aligned} \sum_{v=1}^{V} \log p\left(\boldsymbol{x}^{v}\right) &=\sum_{v=1}^{V} \log \int_{\boldsymbol{z}^{v}} \sum_{c} p\left(\boldsymbol{x}^{v}, \boldsymbol{z}^{v}, \boldsymbol{c}\right) \mathrm{d} \boldsymbol{z}^{v} \\ & \geq \sum_{v=1}^{V} \mathbb{E}_{q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log \frac{p\left(\boldsymbol{x}^{v}, \boldsymbol{z}^{v}, \boldsymbol{c}\right)}{q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\right] \\ &=\sum_{v=1}^{V} \mathcal{L}_{E L B O}\left(\boldsymbol{x}^{v}\right) \end{aligned}

其中LELBO(xv)\mathcal{L}_{E L B O}\left(\boldsymbol{x}^{v}\right)是第v个视图的证据下界(ELBO，evidence lower bound)。在变分推理中，最大化ELBO与最大化可能性是等价的。给定p(xv,zv,c)=p(xv∣zv,c)p(zv,c)p\left(\boldsymbol{x}^{v}, \boldsymbol{z}^{v}, \boldsymbol{c}\right)=p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right) p\left(\boldsymbol{z}^{v}, \boldsymbol{c}\right)，每个视图的ELBO可以使用下面的公式表示：

公式8：LELBO(xv)=Eq(zv,c∣{xv})[log⁡p(xv∣zv,c)]−DKL(q(zv,c∣{xv})∥p(zv,c))公式8：\begin{aligned} \mathcal{L}_{E L B O}\left(\boldsymbol{x}^{v}\right) &=\mathbb{E}_{q\left(\boldsymbol{z}^{v}, c \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\right] \\ &-D_{K L}\left(q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p\left(\boldsymbol{z}^{v}, \boldsymbol{c}\right)\right) \end{aligned}

假设视图公共变量和视图特定变量是条件独立的，则有q(zv,c∣{xv})=q(zv∣xv)q(c∣{xv})q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)=q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right) q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)，先验概率p(zv,c)=p(zv)p(c)p\left(\boldsymbol{z}^{v}, \boldsymbol{c}\right)=p\left(\boldsymbol{z}^{v}\right) p(\boldsymbol{c})。KL散度DKLD_{KL}可以被分为两部分：

公式9：DKL(q(zv,c∣{xv})∥p(zv,c))=Eq(zv,c∣{xv})[log⁡q(zv,c∣{xv})p(zv,c)]=Eq(zv∣xv)Eq(c∣{xv})[log⁡q(zv∣xv)q(c∣{xv})p(zv)p(c)]=Eq(zv∣xv)Eq(c∣{xv})[log⁡q(zv∣xv)p(zv)]+Eq(zv∣xv)Eq(c∣{xv})[log⁡q(c∣{xv})p(c)]=DKL(q(zv∣xv)∣∣p(zv))+DKL(q(c∣{xv})∥p(c))公式9：\begin{array}{l} D_{K L}\left(q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p\left(\boldsymbol{z}^{v}, \boldsymbol{c}\right)\right) \\ =\mathbb{E}_{q\left(\boldsymbol{z}^{v}, c \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log \frac{q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}{p\left(\boldsymbol{z}^{v}, \boldsymbol{c}\right)}\right] \\ =\mathbb{E}_{q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)} \mathbb{E}_{q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log \frac{q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right) q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}{p\left(\boldsymbol{z}^{v}\right) p(\boldsymbol{c})}\right] \\ =\mathbb{E}_{q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)} \mathbb{E}_{q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log \frac{q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)}{p\left(\boldsymbol{z}^{v}\right)}\right] \\ +\mathbb{E}_{q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)} \mathbb{E}_{q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log \frac{q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}{p(\boldsymbol{c})}\right] \\ =D_{K L}\left(q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)|| p\left(\boldsymbol{z}^{v}\right)\right)+D_{K L}\left(q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p(\boldsymbol{c})\right) \end{array}

通过这个方式，cc和zvz^v的KL散度项被分离，这个设计可以用于视图离散化公共表示和视图特定表示。对于第v个视图的目标最大化过程变成：

公式10：LELBO(xv)=Eq(zv,c∣{xv})[log⁡p(xv∣zv,c)]−DKL(q(zv∣xv)∣∣p(zv))−DKL(q(c∣{xv})∥p(c))公式10：\begin{array}{l} \mathcal{L}_{E L B O}\left(\boldsymbol{x}^{v}\right)=\mathbb{E}_{q\left(\boldsymbol{z}^{v}, \boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\right] \\ -D_{K L}\left(q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)|| p\left(\boldsymbol{z}^{v}\right)\right)-D_{K L}\left(q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p(\boldsymbol{c})\right) \end{array}

学习分离表征

KL散度项是潜在变量和数据之间的交互信息的上界。为了离散化模型的视图公共表示和视图特定表示，每个潜在变量应该编码更多的变量信息。因此在公式10中KL散度项的通道容量应该逐渐增加，定义用于视图公共变量和视图特定变量的KL散度项的控制容量分别为CcC_c和CzC_z。第v个视图的ELBO可以被表示为：

公式11：LELBO(xv)=Eq(zv,c∣{xv})[log⁡p(xv∣zv,c)]−β∣DKL(q(c∣{xv})∥p(c))−Cc∣−β∣DKL(q(zv∣xv)∥p(zv))−Cz∣公式11：\begin{aligned} \mathcal{L}_{E L B O}\left(\boldsymbol{x}^{v}\right) &=\mathbb{E}_{q\left(\boldsymbol{z}^{v}, c \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\right] \\ &-\beta\left|D_{K L}\left(q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p(\boldsymbol{c})\right)-C_{c}\right| \\ &-\beta\left|D_{K L}\left(q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right) \| p\left(\boldsymbol{z}^{v}\right)\right)-C_{z}\right| \end{aligned}

其中β\beta是权衡置信度。当p(c)p(c)为均匀类别分布(uniform categorical distribution)时，对于视同公共变量的KL散度是有界的：

公式12：DKL(q(c∣{xv})∥p(c))=∑i=1Kqilog⁡qipi=∑i=1Kqilog⁡qi1/K=−H(q)+log⁡K≤log⁡K公式12：\begin{aligned} D_{K L}\left(q\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p(\boldsymbol{c})\right) &=\sum_{i=1}^{K} q_{i} \log \frac{q_{i}}{p_{i}}=\sum_{i=1}^{K} q_{i} \log \frac{q_{i}}{1 / K} \\ &=-H(q)+\log K \leq \log K \end{aligned}

其中HH表示熵，基于这个，令Cc=logKC_c=logK，他控制了c中编码的变分信息的最大容量。考虑不同的视图有不同的数据重建损失规模，因此进一步引入β\beta去平衡所有视图的离散性。对于第v个视图，权重可以计算为：

公式13：βv=βEq(zv,c∣{xv})[log⁡p(xv∣zv,c)]max⁡vEq(zv,c∣{xv})[log⁡p(xv∣zv,c)].公式13：\beta^{v}=\beta \frac{\mathbb{E}_{q\left(\boldsymbol{z}^{v}, c \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\right]}{\max _{v} \mathbb{E}_{q\left(\boldsymbol{z}^{v}, c \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\right]} .

总共的损失函数由三个部分组成：

公式14：Lloss =−∑v=1VLELBO(xv)=∑v=1Vβv∣DKL(q(c∣{xv})∥p(c))−Cc∣+∑v=1Vβv∣DKL(q(zv∣xv)∣∣p(zv))−Cz∣−∑v=1VEq(zv,c∣{xv})[log⁡p(xv∣zv,c)]公式14： \begin{array}{l} \mathcal{L}_{\text {loss }}=-\sum_{v=1}^{V} \mathcal{L}_{E L B O}\left(\boldsymbol{x}^{v}\right)\\ =\sum_{v=1}^{V} \beta^{v}\left|D_{K L}\left(q\left(c \mid\left\{\boldsymbol{x}^{v}\right\}\right) \| p(\boldsymbol{c})\right)-C_{c}\right|\\ +\sum_{v=1}^{V} \beta^{v}\left|D_{K L}\left(q\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)|| p\left(\boldsymbol{z}^{v}\right)\right)-C_{z}\right|\\ -\sum_{v=1}^{V} \mathbb{E}_{q\left(z^{v}, c \mid\left\{\boldsymbol{x}^{v}\right\}\right)}\left[\log p\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\right] \end{array}

其中，第一项和第二项的优化用于学习离散的视图公共表示和视图特定表示。第三项是可能性项，优化去保持VAE的重构质量。

Multi-VAE-C

从结构图中可以看出，所有的特征可以被分为{c,z1,z2,…,zV}\left\{c, z^{1}, z^{2}, \ldots, z^{V}\right\}，每一组{c,zv}\left\{c, z^{v}\right\}用于重建特征。通过这种方式，每个视图的特定视觉信息可以通过视觉特定表示zvz^{v}提取，反过来，所有视图的共同聚类信息也可以通过视图公共表示cc提取。因为cc是one-hot形式的近似表示，第i个样本的聚类预测可以通过下面的式子进行计算：

公式15：yi=arg⁡max⁡j(cj)=arg⁡max⁡j(qϕ(cj∣{xiv})).公式15：y_{i}=\arg \max _{j}\left(\boldsymbol{c}_{j}\right)=\arg \max _{j}\left(q_{\phi}\left(\boldsymbol{c}_{j} \mid\left\{\boldsymbol{x}_{i}^{v}\right\}\right)\right) .

Multi-VAE-CZ

给定多视图视觉信息在用于聚类时是互补的，将分离的特征缩放到[0,1][0,1]，拼接他们去形成一个全局的潜在表示[c;{zv}]\left[c ;\left\{z^{v}\right\}\right]，然后将其输入到K-means中，从而获得另一个聚类预测。

优化Multi-VAE的算法

输入：多视图数据集{xi1,xi2,...,xiV}i=1N\{\mathbf{x}_i^1,\mathbf{x}_i^2,...,\mathbf{x}_i^V\}_{i=1}^N，聚类数KK，权衡置信度β\beta，最大控制容量CzC_z，Cc=logKC_c=logK，随机初始化参数ϕ\phi和{ϕv,θv}v=1V\{\phi^v,\theta^v\}^V_{v=1}

while 没有到达最大迭代次数 do：

  1. 通过编码器计算{sk}k=1K\{s^k\}_{k=1}^K和{μv,δv}v=1V\left\{\boldsymbol{\mu}^{v},\boldsymbol{\delta}^{v}\right\}_{v=1}^{V}
  2. 使用带有参数化技巧的公式2和公式4推理qϕ(c∣{xv})q_{\phi}\left(\boldsymbol{c} \mid\left\{\boldsymbol{x}^{v}\right\}\right)和qϕv(zv∣xv)q_{\phi^{v}}\left(\boldsymbol{z}^{v} \mid \boldsymbol{x}^{v}\right)
  3. 通过解码器生成{pθv(xv∣zv,c)}v=1V\{p_{\theta^{v}}\left(\boldsymbol{x}^{v} \mid \boldsymbol{z}^{v}, \boldsymbol{c}\right)\}^V_{v=1}
  4. 通过最小化公式14更新ϕ\phi和{ϕv,θv}v=1V\{\phi^v,\theta^v\}_{v=1}^V

end while

输出：离散的表征cc和{zv}v=1V\{z^v\}^V_{v=1}

实验方式

使用指标：聚类准确率ACC，归一化互信息NMI，调整兰德系数ARI，纯度Purity

  1. 在MNIST,Fashion，Product以及COIL上对比了Multi-VAE和其他SOTA的方法
  2. 可视化视图公共表征cc和一些视图的视图特定表征zvz^v，证实模型确实将这些特征离散化了
  3. 展示使用不同的视图表示（公共表示和每一个视图的特定表示）随着迭代次数的增加NMI指标的变化图，说明了公共表示c用于聚类的有效性。同时可视化了聚类过程。
  4. 通过使用提出的结构加上vanilla VAE，不使用控制容量，只使用视图特定表征的控制容量CzC_z，只使用视图公共表征的控制容量CcC_c，以及完整的结构进行消融实验。
  5. 分析了权衡置信度β\beta和视图特定变量的最大控制容量CzC_z的敏感度，结论是这两个参数对模型并不敏感。