「论文阅读(简)」Graph Attention Network
作者:Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, Yoshua Bengio
时间:2018
期刊或会议:ICLR
原文摘要
We present graph attention networks (GATs), novel neural network architectures that operate on graph-structured data, leveraging masked self-attentional layers to address the shortcomings of prior methods based on graph convolutions or their approximations. By stacking layers in which nodes are able to attend over their neighborhoods’ features, we enable (implicitly) specifying different weights to different nodes in a neighborhood, without requiring any kind of costly matrix operation (such as inversion) or depending on knowing the graph structure upfront. In this way, we address several key challenges of spectral-based graph neural networks simultaneously, and make our model readily applicable to inductive as well as transductive problems. Our GAT models have achieved or matched state-of-the-art results across four established transductive and inductive graph benchmarks: the Cora, Citeseer and Pubmed citation network datasets, as well as a protein-protein interaction dataset (wherein test graphs remain unseen during training).
理论基础
- 谱方法使用图的谱表示,并已经成功应用与节点分类。在傅里叶域中计算图拉普拉斯的特征分解来定义卷积操作,这个过程设计到大量的密集计算,增大了计算复杂度。
- 非谱的方法面对的一些挑战是去定义一个操作,他可以处理不同大小的邻居,并保持CNN的权重共享属性。
- 当注意力机制用于捕获一个单一序列的表征时,他通常被称为自注意力或内部注意力。
任务与存在的问题
- CNN处理的数据通常是grid-like的结构,而许多有趣的任务涉及的数据不能用grid-like的结构进行表示,他们位于一个不规则的域中。比如:3D网格,社交网络,电信网络,生物网络以及大脑连接体。
主要工作与创新点
提出了基于注意力的结构用于执行图结构数据的节点分类任务。其思想是通过关注他的邻居,并遵循自注意力的策略,计算图中每一个节点的隐藏表示。这个注意力结构有几个有趣的属性:
- 这个操作是有效的,因为他可以跨节点-邻居对(node-neighbor pairs)进行优化。
- 他可以通过指定对邻居的任意加权应用于有不同度的图节点
- 该模型直接适用于归纳学习问题,包括模型必须推广到完全看不见的图的任务。
在使用GAT时,图的结构不要求是无向图,如果不存在一条边,则可以不计算他的
提出的方法
图注意力层
图注意力层的输入是节点特征的集合,,其中是节点的数量,是每个节点的特征数量。图注意力层输出产生新节点特征集合(可能有不同的维度),。
为了获得强大的表达能力,以实现输入特征向高级特征的转换,本文设置了一个初始化步骤,其是一个共享的线性转换,他的参数是一个权重矩阵,并将这个线性转换应用在每一个节点上。然后在节点上执行自注意力,这是一个共享的注意力机制:来计算注意力系数:
其表示节点j对节点i的重要性。这是最简单的公式,他忽略了图的结构信息,本文对这个机制通过执行掩码注意力将图结构注入其中。掩码注意力只为节点计算,其中是图中节点i的邻居集合。其中这个邻居集合是一阶与节点i近邻的。为了使系数更容易在不同的节点上进行对比,于是本文通过softmax归一化了j的所有选择:
注意力机制是一个单层前馈神经网络,权重向量,并应用LeakyReLU作为非线性激活函数(负输入的斜率为0.2)。将其与公式2结合,可以得到下面的公式(图1的左边也可以形象地说明计算过程):
其中表示转置,是concate操作。
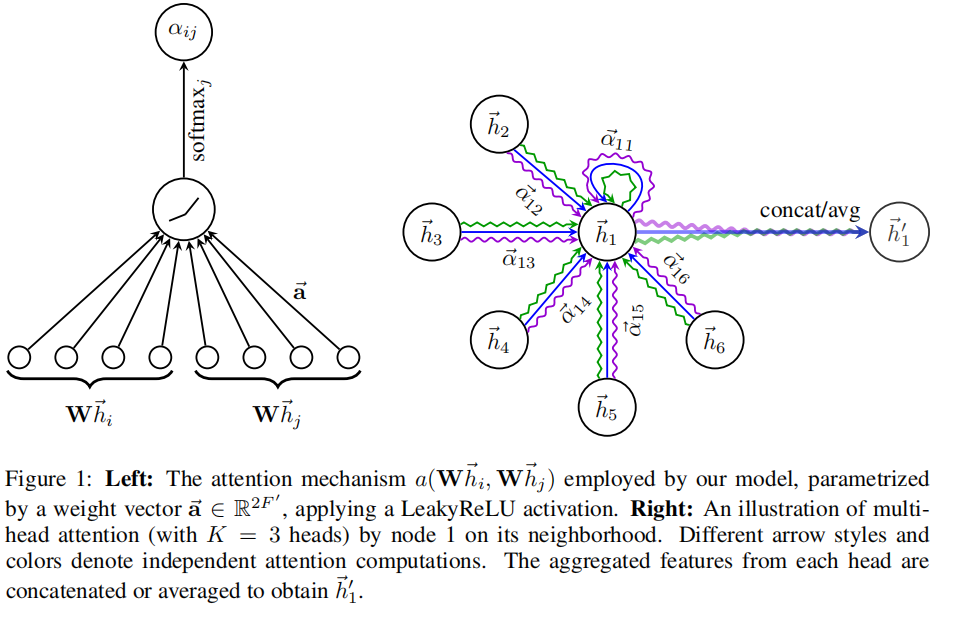
这个归一化的注意力系数用于计算与他们对应的特征的线性组合,以作为每个节点的最终输出特征(使用一个非线性变化)。
为了稳定地训练这个自注意力,本文通过多头注意力去拓展这个机制。具体来说个独立的注意力机制执行公式4的转换,然后他们的特征被concat,从而产生了下面公式的特征表示:
其中表示连接,是由第k个注意力机制计算的归一化注意力系数。是对应的输入线性变换的权重矩阵。值得注意的是,通过这种方式得到的在每个节点的输出由个特征组成而不是个。
在网络的最后一层(预测层)中执行的多头注意力不再使用concate,而是使用averaging,并延迟应用与最终的非线性激活(对于分类任务通常是softmax或者logistic sigmoid):
这个多头图注意力层的聚合过程展示在图1的右边。
实验方式
使用的数据集情况如下:
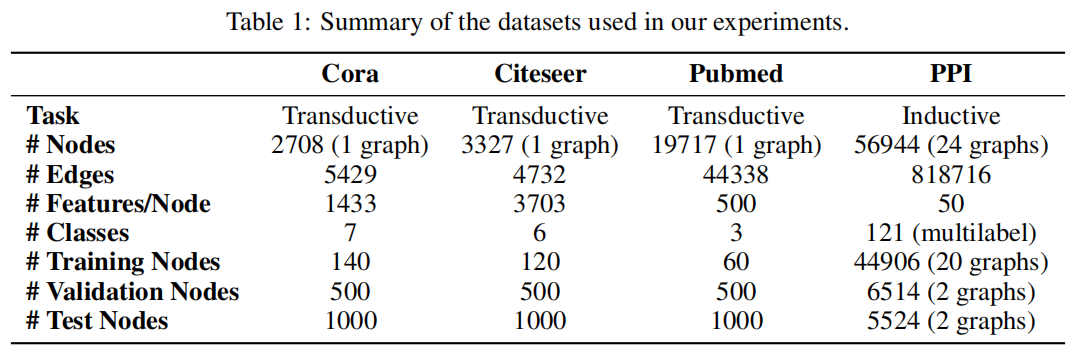
直推学习(对应数据集Cora,Citeseer,Pubmed)和归纳学习(PPI)的方法进行对比。使用平均分类准确率作为指标。








