论文名称:Semi-Supervised Classification with Graph Convolutional Network
作者:Kipf, Thomas N., Max Welling
时间:2017年
期刊或会议:ICLR
代码:https://github.com/dragen1860/GCN-PyTorch
原文摘要
We present a scalable approach for semi-supervised learning on graph-structured data that is based on an effificient variant of convolutional neural networks which operate directly on graphs. We motivate the choice of our convolutional architecture via a localized fifirst-order approximation of spectral graph convolutions. Our model scales linearly in the number of graph edges and learns hidden layer representations that encode both local graph structure and features of nodes. In a number of experiments on citation networks and on a knowledge graph dataset we demonstrate that our approach outperforms related methods by a signifificant margin.
理论基础
- 标签只适用于一小部分的节点子集这个问题可以通过构建一个基于图的半监督学习,这使得标签可以通过使用一些形式的显式的图正则化,比如在损失函数中加入图拉普拉斯正则化项:
公式1:L=L0+λLreg, with Lreg=i,j∑Aij∥f(Xi)−f(Xj)∥2=f(X)⊤Δf(X)
其中L0表示图中有标签部分的监督损失,f(⋅)是类似神经网络的可微函数,λ是权重因子,X是节点特征向量Xi的矩阵。Δ=D−A表示无向图G=(V,E)(其有N个节点vi∈V,边(vi,vj)∈E,邻接矩阵A∈RN×N,度矩阵Dii=∑jAij)的非标准化图拉普拉斯矩阵。
任务与存在的问题
- 在图上的节点分类任务(知识图谱中的文档分类)存在问题:标签只适用于一小部分的节点子集。
- 在公式1中依赖一个假设:图上连接的节点是共享相同标签的。但这个假设可能会限制建模能力,因为图的边不需要编码节点的相似性,但可能包含额外的信息。
主要工作
提出了一个在图结构数据上的用于半监督学习的可伸缩的方法,其是卷积神经网络的一个有效变体,可以直接在图上操作。通过谱图卷积的局部一阶近邻来激发卷积体系结构的选择。
创新点
- 针对直接作用于图的神经网络模型,引入了一种简单且行为良好的分层传播规则,展示如何从谱卷积的一阶近似中激发他。
- 展示了这种形式的基于图的神经网络如何用于图中节点的快速和可拓展的半监督分类。
在图上的快速近似图卷积
多层GCN可以根据下面的分层传播规则计算:
公式2:H(l+1)=σ(D~−21A~D~−21H(l)W(l)).
其中A~=A+IN是添加了自环的无向图G的邻接矩阵。IN是单位矩阵,D~ii=∑jA~ij和W(L)是特定层中可以被训练的权重矩阵。σ(⋅)表示激活函数。ReLU(⋅)=max(0,⋅).H(l)∈RN×D是在第l层激活后的矩阵。H(0)=X。
谱图卷积
本文将在图上的谱图卷积当做在傅里叶域中,使用通过θ∈RN参数化过的滤波器gθ=diag(θ)和一个信号x∈RN(每个节点的标量)的矩阵乘法,可以用下面的公式表示:
公式3:gθ⋆x=UgθU⊤x
其中U是归一化的图拉普拉斯矩阵L=IN−D−21AD−21=UΛU⊤的特征向量矩阵,这个图拉普拉斯矩阵有一个特征值为Λ的对角矩阵,U⊤x是x的图傅里叶变化。可以将gθ理解为L的特征值的一个函数,比如gθ(Λ)。由于特征向量矩阵U的乘法运算是O(N2)的,因此在大型图中计算L的特征分解代价很大。为了解决这个问题,gθ(Λ)可以用切比雪夫多项式Tk(x)的阶段展开来近似代替:
公式4:gθ′(Λ)≈k=0∑Kθk′Tk(Λ~)
重新调整的Λ~=λmax2Λ−IN。λmax表示L最大的特征值。θ′∈RK是切比雪夫系数的一个向量。q切比雪夫多项式的递归定义为:Tk(x)=2xTk−1(x)−Tk−2(x)
因此公式3可以根据公式4近似表示为
公式5:gθ′⋆x≈k=0∑Kθk′Tk(L~)x
其中L~=λmax2L−IN,(UΛU⊤)k=UΛkU⊤,这个表达式现在是K-localized的,因为他是拉普拉斯行列式中的第一个K阶多项式。比如,他只依赖于距离中心节点(K阶邻域)最大K阶的节点。
分层线性模型
在GCN的线性公式中,进一步近似λmax≈2,在这个近似下,公式5可以简化为:
公式6:gθ′⋆⋆x≈θ0′x+θ1′(L−IN)x=θ0′x−θ1′D−21AD−21x
其中θ0′和θ1′是两个自由的参数,滤波器参数可以在整张图上共享。
实际上进一步约束参数量对解决过拟合问题和最小化每一层的操作数量是有益的,于是又了下面的式子:
公式7:gθ⋆x≈θ(IN+D−21AD−21)x,
其中参数θ=θ0′=−θ1′,注意IN+D−21AD−21现在有在[0,2]之间的特征值。重复使用这个操作会是使得深度神经网络模型参数不稳定,梯度爆炸和梯度消失。为了减轻这个问题,使用了renormalization技巧:IN+D−21AD−21→D~−21A~D~−21,其中A~=A+IN,D~ii=∑jA~ij。
于是可以形成对于一个有C个输入通道(每个节点又C维的特征向量)和F利波器或特征映射的信号X∈RN×C的定义如下:
公式8:Z=D~−21A~D~−21XΘ,
其中Θ∈RC×F是滤波器参数矩阵,Z∈RN×F是卷积信号矩阵。
半监督节点分类
引入以简单灵活的模型f(X,A),用于在图上有效地传播信息。对于半监督节点分类问题,可以通过将模型f(X,A)对数据X和底层图结构的邻接矩阵A进行调整,拉放松基于图的半监督学习中所做的某些假设。期望这种方法在邻接矩阵包含数据X中不存在的信息的场景中有强大的表现。整个模型是一个用于半监督学习的多层GCN,如下图所示:
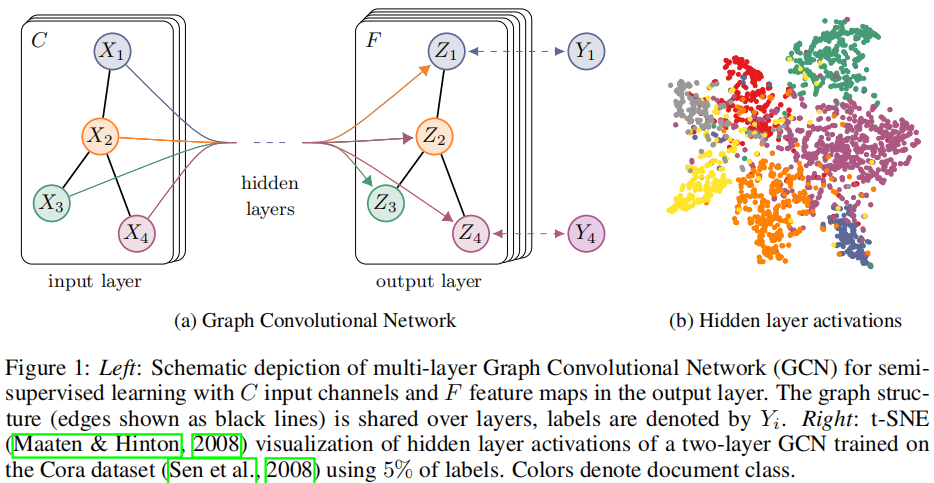
使用对称邻接矩阵A在图上使用一个两层的GCN进行半监督图节点分类。首先,在预处理步骤中计算A^=D~−21A~D~−21,然后,前向模型可以用下面的公式表示:
公式9:Z=f(X,A)=softmax(A^ReLU(A^XW(0))W(1))
其中W(0)∈RC×H具有H特征映射的隐藏层的input-to-hidden权重矩阵。W(1)∈RH×F是hidden-to-output的权重矩阵。softmax的计算公式为:softmax(xi)=Z1exp(xi)其中Z=∑iexp(xi)。对于半监督多类别分类任务,会在所有标记的样本上的交叉熵误差进行评估:
公式10:L=−l∈YL∑f=1∑FYlflnZlf,
其中YL有标签的节点索引集。
实验方式
数据集使用情况如下:
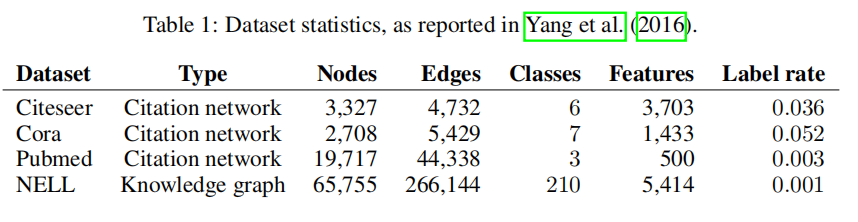
- 对在引用网络中进行半监督文档分类任务,对从知识图谱中提取的二分图进行半监督实体分类任务,对各种图传播模型的评估和对随机图的运行实时分析任务进行了大量的实验。
- 使用公式5,6,7,8不同的前向传播方式,实现GCN
(ps:代码的话可以看看我贴在开头的那个仓库,pytorch版本的,GCN的结构比较清晰,缺点是数据已经封装好了,没注意到数据怎么构建,用了很多sparse的方法)











