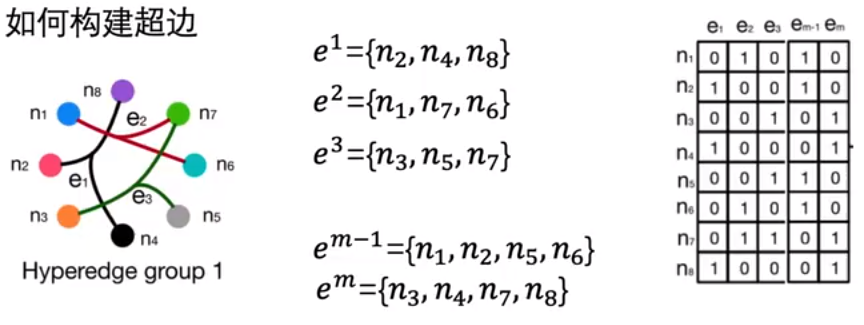视频学习笔记:https://www.bilibili.com/video/BV1334y1571g?spm_id_from=333.337.search-card.all.click
异构图
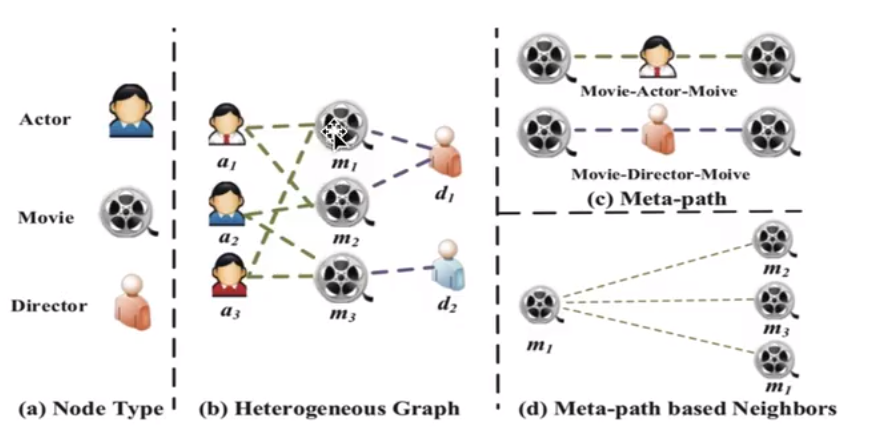
包含不同类型节点和连接
异构图的定义:节点类别的数量加上边的类别的数量大于2
元路径(Meta-path):是连接两个对象的复合关系,是一种广泛使用的捕获语义的结构,比如,电影——演员——电影,这样的一个连接
基于元路径的邻居(Meta-path based Neighbors):通过Meta-path找到的邻居信息
Heterogeneous Graph Attention Network(HAN)
这个算法主要包含了两个重要的计算方式,一个是节点级别的注意力(Node-level Attention),另一个是语义级别的注意力(Semantic-level Attention)。
节点级别的注意力:对于原本给定的图结构,按照不同的元路径的定义,将其转化成另一种不同的图。举个例子,一张图的节点只有红和蓝两种颜色,定义一种元路径为红-蓝-红,然后根据这个元路径,利用基于元路径的邻居定义转化成一张只有红色节点的图,然后在这张图上对每一个节点,计算其与邻居的注意力,然后使用softmax进行归一化,然后将每个节点加权求和作为这个节点的新的表征(这个操作和GAT基本一致,当然也支持多头注意力的使用)。将每个节点更新完整后,将这些表征拼接起来,形成这个元路径的表征。
语义级别的注意力:这里主要是使用不同元路径定义的表征进行计算。对于每一个元路径定义的表征的每一个节点表征都做一个MLP(MLP参数共享)的操作,然后进行加权求和取平均从而获得这个元路径的权重,然后将每个元路径的权重都计算完成后,使用softmax的方式归一化每一个权重,得到的新权重,就是语义级别的权重。最后对于图上每个节点的新表示,则可以使用不同元路径定义下的节点表征乘上对应的语义级别权重的求和获得。
在实际使用过程中,可能会出现节点的特征数量不一致的情况,这个在开始节点级别的注意力之前,通常都会进行一个映射的操作,使得每个节点的特征数量保持一致。
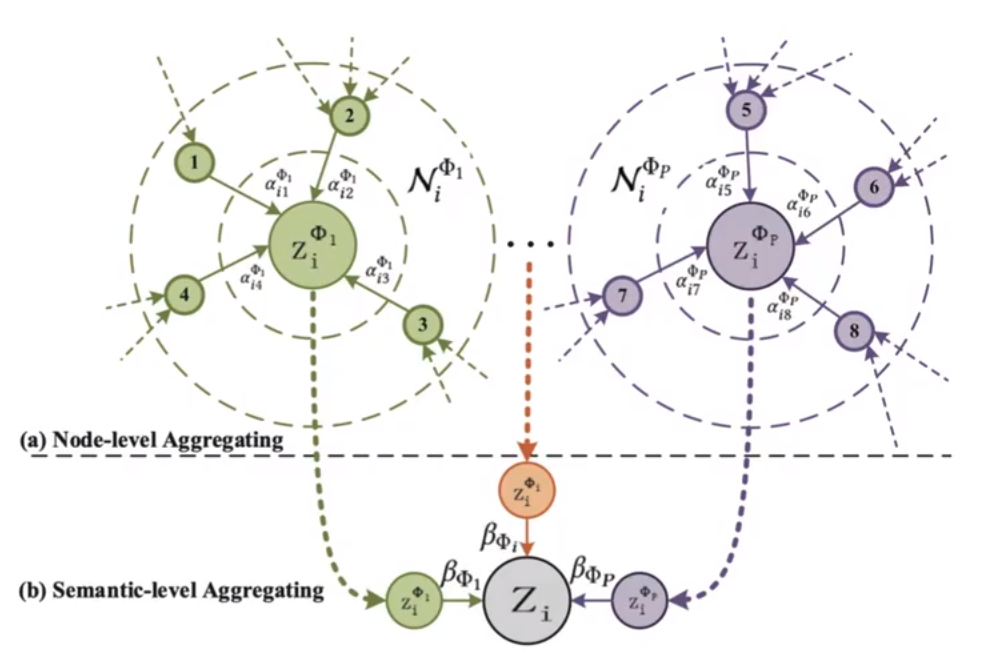
这个算法可以使用下面的图进行表示,首先在a一行中,不同颜色表示不同的元路径定义形成的图,αi1ϕ1表示的是与目标节点在ϕi元数据定义中与目标Zi相邻的节点计算出的节点级别注意力(和GAT中的α基本一致)。然后βϕi表示语义级别的权重,最终Zi的新表示就是不同元路径定义下的Zi与对应元路径定义下的语义级别权重的加权和。
GTN能够识别原始图上未连接节点之间的有用连接,同时在端到端学习新图上的有效节点的表示。HAN通过将异构图转化为由元路径构造的齐次图来学习图表示学习,但是,这些方法由邻域专家手动选择元路径,因此可能无法捕获每个问题的所有有意义的关系,同样,元路径的选择也会显著影响性能。而GTN可以在异构图上生成任务转化图,同时以端到端的方式学习转换图上的节点表示。
这次使用ACM数据集进行说明:Paper(3025),Author(5835),Subject(56)
τv和τe分别是节点类型集合和边的类型集合,比如节点在ACM中有Paper,Author,Subject三个类,而这个图是无向图,边的类型就会有Paper->Author,Autrhor<-Paper,Paper->Subject,Subject->Paper这四个关系(由于数据集中没有Author和Subject的边,所有没有这个类型)。后面这三个类别会简写为P,A,S。
邻接矩阵:
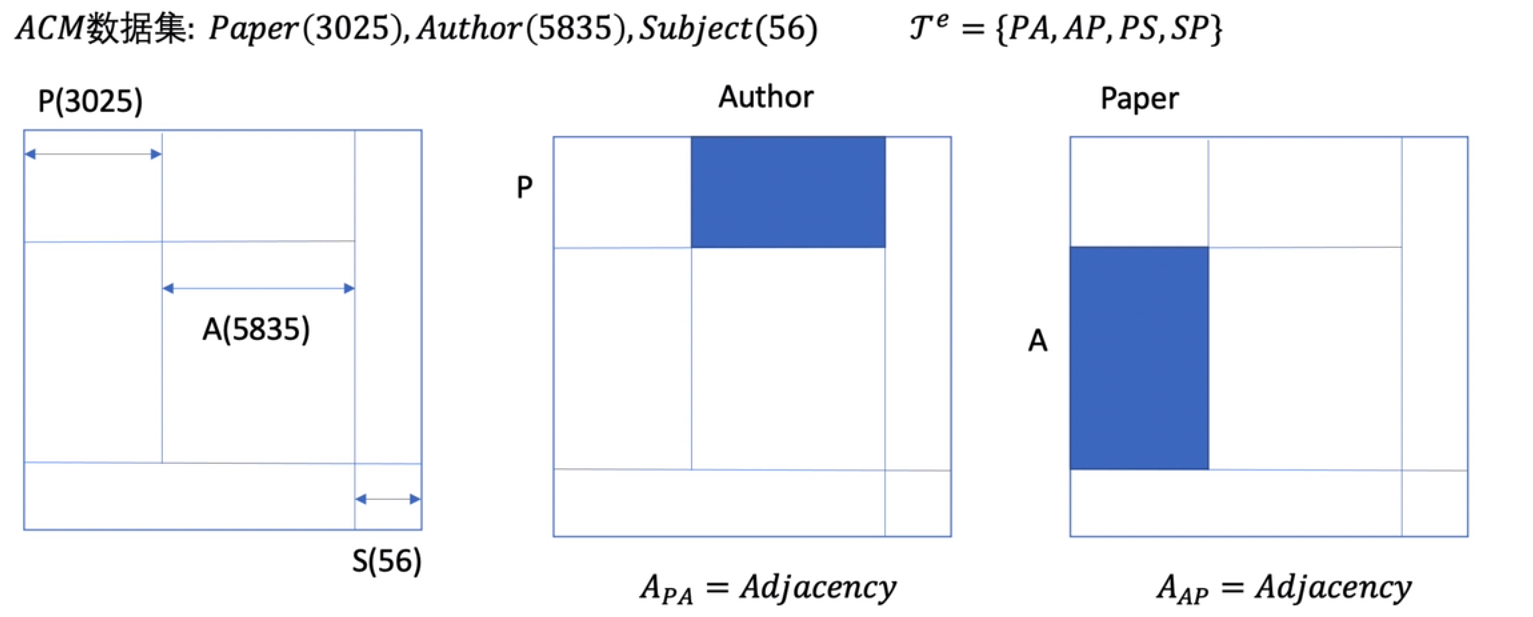
如上图,直接把所有节点列出来,形成NxN的矩阵,然后对于边为PA(Paper->Author)类型的如图中第二个图,蓝色部分的地方是有值的,其他地方都是0
特征矩阵:X∈RN×D,其中D表示维度,在数据集中只有Paper是有特征的,那么Author和Subject的特征可以通过拼接paper的方式构建(当然,也可以求和,取最大值等等),然后将构建好的特征拼接在一起形成特征矩阵,如下图:

GTN组合多元元路径的范式:
meta−path={PAP}={PA,AP}=AdjPA×AdjAP
就是矩阵相乘的一个方式就可以构建出多元元路径,可以看到PAP之间是有一个A相连的,乘积出来的邻接矩阵才有意义,但是如果是PA和PA相乘则没有意义。
算法结构图:
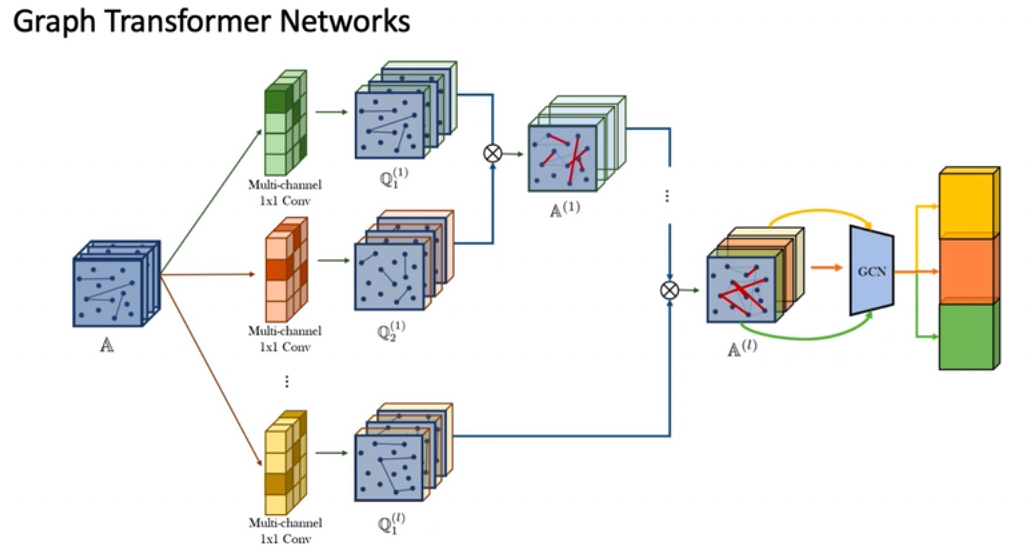
A是经过之前说的多元元路径构造出的多个邻接矩阵的拼接结果,然后使用1×1的卷积方式对A的每一层进行加权,然后得到Q这个新的矩阵,然后这些矩阵两两相乘,最终获得要输入到GCN层中的邻接矩阵,然后输出特征。这个操作的含义就是可以自动地生成元路径构造出来的图,然后在GCN中野可以利用这些图构造不同的特征信息,从而达到一个节点分类的目的。
Attributed:节点属性,用户,商品
Multiplex:用户和item之间的边可以浏览,点击,添加到购物车,购买等。
解决这种异构图的方法
- HON(同构网络),忽略了节点和边的属性,结果较差
- MHEN(不考虑节点性质的异构网络),结果还不错(GATNE)
- AMHEM(考虑多种类型,节点性质的异构图网络),结果比MHEN好一些
GATNE: General Attributed Multiplex Heterogeneous Network Embedding
GATNE中提出了两种方法,一个是直推式的方法GATNE-T,另一种是具有推理性的方法GATNE-I。这个方法的结构图如下
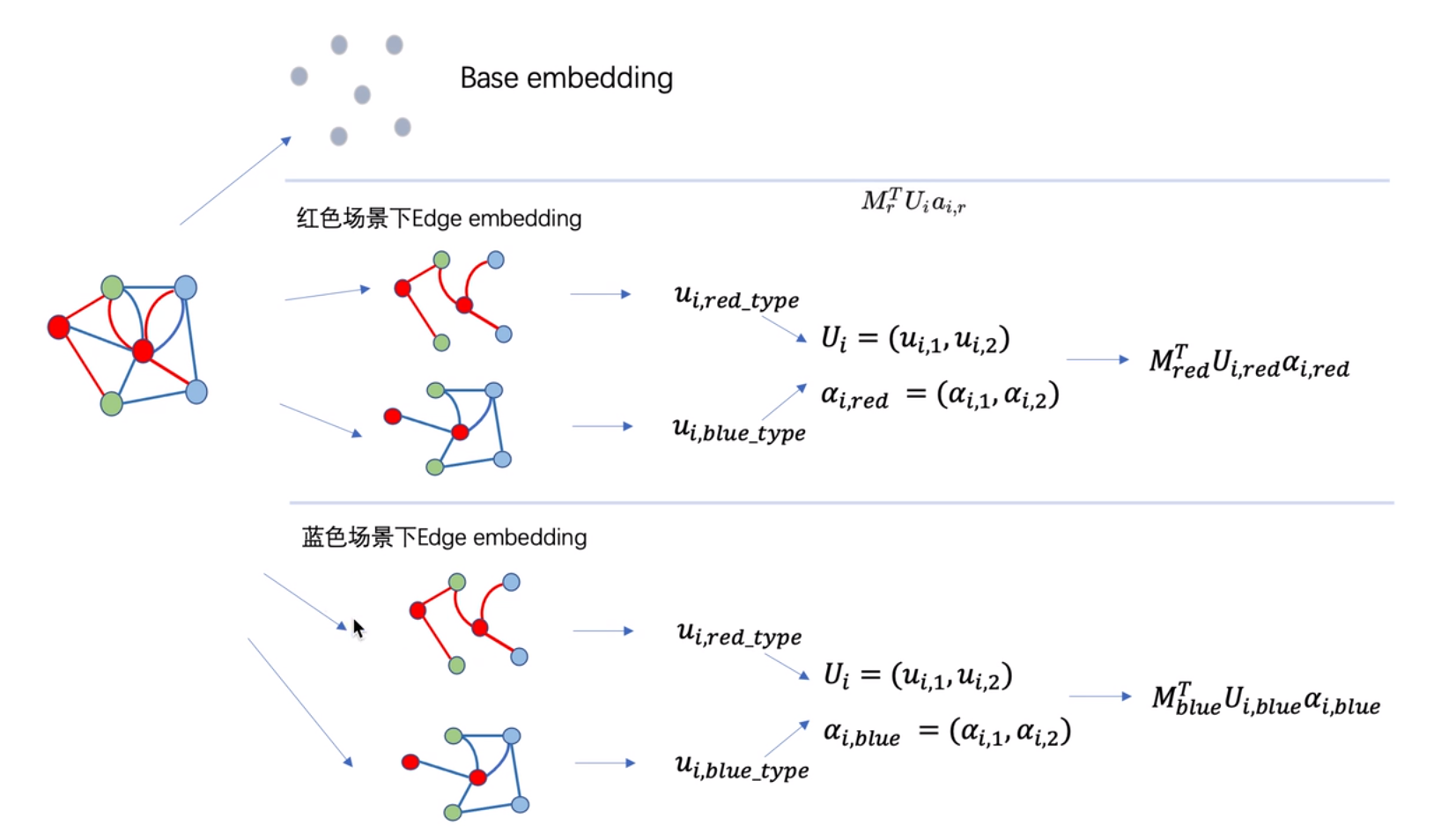
首先需要将图像中的所有边都去掉,然后只针对节点生成embedding,称为base embedding,这里通常是使用MLP的方式进行生成。
在这个图中不同类型的边,表示不同场景下的影响。以红色场景为例子,接着就要将原始的图,按照不同的场景进行拆分,分别叫做红色图和蓝色图,然后分开求Edge embedding。首先是初始化红色图下每个节点的embedding,然后采用邻居聚合的思想,对每一个节点vi的第k阶邻居进行聚合,得到 edge embedding ui,red_type,然后在蓝色图中,再次初始化每个节点的embedding,采用相同的方式得到edge embedding ui,blue_type。接着将这两个edge embedding进行拼接得到整个红色场景下的embedding聚合 Ui,对Ui乘上一个可学习的权重,加一个tanh激活,然后再乘一个可学习的权重wr,加一个softmax得到红色场景下的注意力,拆开来看的话,就是红色图和蓝色图拼接在一起的注意力ai,r。最后计算红色场景下的Edge embedding(注意大写E和小写e的区别)为MrTUiai,r,其中MrT是一个红色场景下可学习的参数。现在已经有了base embedding和Edge embedding,最终得到节点vi,边类型为红色的节点向量可表示为vi,r=bi+αrMrTUiai,r,其中bi为节点i的base embedding,αr为超参数控制edge embedding的重要程度。
同样的方法,也可以得到边类型为蓝色的节点向量表示。在预测阶段主要就是走在上面的红场景和蓝场景中的一个流程,从而得到输出结果。
之前提到了GATNE有两种实现方式,两种实现方式可以用下面的公式表示
GATNE−T:vi,r=bi+αrMrTUiai,rGATNE−I:vi,r=hzxi+αrMrTUiai,r+βrDzTxi
其中hz()表示计算xi的base embedding的一个函数,所以GATNE-I中的hz(xi)与GATNE-T中的bi基本相等。然后在GATNE-I中主要可能面向没有见过的节点,这时候Ui的初始化过程可能也不确定于是可以引入一个初始化函数gz,r来进行初始化,也就是说GATNE-I中的节点初始化gz,r(xi)与GATNE-T中的ui,r(0)等价。最后还引入了一个项βrDzTxi,其中βr是学习的系数Dz也是一个vi对节点类型为z的一个可学习的转化矩阵。
二部图
二部图也可以叫做二分图,其节点可以分为两类,每一类内部是没有边连接的,类与类之间是有边连接的。
显示关系:图中可以看到的边,即不同类别之间的链接情况
隐式关系:图中没有看到边,但是可以通过边的传递性(最多传递一次)进行连接,即类别之间的链接情况。
BINE: Bipartite Network Embedding
通过观察到的显式关系和未观察到的隐式关系,通过优化显式和隐式两个任务来共同学习定点的embedding向量。
显式关系建模:
分别计算边和节点的分布,对于节点vi,uj(表示二部图中的两个类别内的节点),有边wij,那么显式建模出的边的分布为P(i,j)=∑eij∈Ewijwij。接着计算节点的分布P^(i,j)=1+exp(−uiTvj)1,主要用于估计embedding中两个定点之间的局部接近度。目标函数是最小化两个分布的距离,这里采用的就是KL散度的一股计算方式
minimize O1=KL(P∥P^)=∑eij∈EP(i,j)log(P^(i,j)P(i,j))∝−∑eij∈EwijlogP^(i,j).
隐式关系建模:
隐式关系主要是只类间通过传递表示的关系,对于U类的节点ui,uj的隐式关系可以表示为wijU=∑k∈Vwikwjk,k是另一个类U的节点编号,这样就可以获得类间的边表示了。这种操作可以使用矩阵相乘的方式进行简化。在搞糟了两个类的隐式图之后,会在这个网络中进行随机游走(论文中的随机游走,与之前的随机游走不太一样,在这篇文章中,中心性越高的节点随机游走的次数就越多,同时并不会固定游走长度,而是随机长度),构造了相同类型定点之间的二阶接近度。然后使用skip-gram和负采样计算节点的embedding。具体建模过程如下:
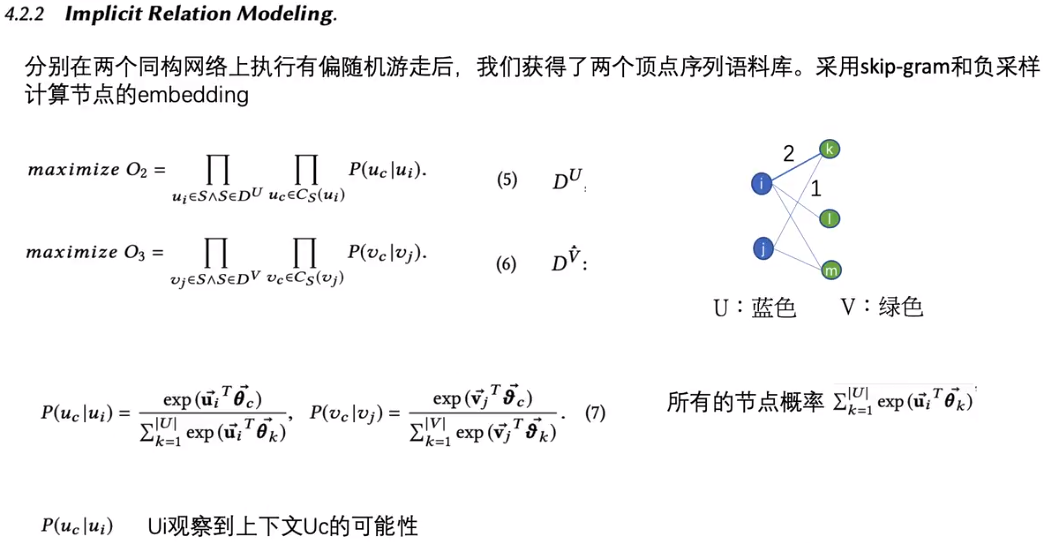
最后的目标函数为
maximize L=αlogO2+βlogO3−γO1
节点的显示关系更新为:
uivj=ui+λ{γwij[1−σ(uiTvj)]⋅vj}=vj+λ{γwij[1−σ(uiTvj)]⋅ui}
隐式更新为
uivj=ui+λ⎩⎨⎧z∈{uc}∪NSns(ui)∑α[I(z,ui)−σ(uiTθz)]⋅θz⎭⎬⎫=vj+λ⎩⎨⎧z∈{vc}∪NSns(vj)∑β[I(z,vj)−σ(vjTϑz)]⋅ϑz⎭⎬⎫
符号图
符号图带来的挑战主要集中在负向链接,与正向链接相比,他不仅具有不同的语义,而且原理本质上是不同的,并且他们与正向链接形成了复杂关系
符号图的定义G=(u,E+,E−)其中E+和E−分别表示正向边和负向边,并且E+⋂E−=∅,说明边要么正向要么负向
我们要解决的挑战是:
- 如何处理负向连接,他们的属性和正向连接完全不同
- 如何将正负连接组合一个模型,以更好地学习点的表征
Signed Graph Convolutional Network(SGCN)
平衡理论:将节点集分成平衡节点和非平衡节点,对于某一个中心节点,对于一阶的平衡节点集就是与中心节点使用正向边相连的的节点,非平衡节点集就是与中心节点使用负向边向量的节点。在往外括一层,即二阶平衡节点集,则再下一层中,与一阶中加入的所有节点同为正向或同为负向的节点,加入到平衡节点集中,否则,加入到非平衡节点集。
根据这个平衡理论在SGCN中,在第一层会求出每个节点的平衡特征和非平衡特征。对于平衡特征其计算方式为:将当前节点与该节点在第一层的平衡节点集中的节点特征求和取平均的结果进行拼接,然后乘一个可学习的参数,然后加个激活,获得第一层的平衡特征。对于非平衡特征,则也是类似的方式,将当前节点与该节点在第一层的非平衡节点集中的节点特征求和取平均的结果进行拼接,乘可学习参数+激活。这就完成了第一层的结果。
按照第一层的方式计算完所有节点的平衡和非平衡特征后,进行第二层的节点计算。对于平衡特征的计算,则是先计算与目标节点相邻的正向边链接的节点的第一层平衡特征的平均值,然后计算与目标节点相邻的负向边连接的节点的第一层非平衡特征的平均值,将这个两个平均值与该节点在第一层的平衡特征进行拼接,可学习权重加权,激活后得到第二层的平衡特征。对于非平衡表征也基本类似,只是对于正向边连接的时候用的是第一层的非平衡特征,负向边相连的时候用的是第一层的平衡特征,然后将两个平均值与该节点在第一层的非平衡特征进行拼接,可学习权重加权,激活得到第二层的非平衡特征。用公式可以表示为:
hiB(l)=σ(WB(l)[∑j∈Ni+∣Ni+∣hjB(l−1),∑k∈Ni−∣Ni−∣hkU(l−1),hiB(l−1)])hiU(l)=σ(WU(l)[∑j∈Ni+∣Ni+∣hjU(l−1),∑k∈Ni−∣Ni−∣hkB(l−1),hiU(l−1)])
最后将平衡和非平衡特征尽心拼接,作为最后节点的embedding。
SiGAT
利用平衡理论和地位理论,提出了Motifs方法来提取节点邻居,并使用GAT的方法去解决邻居聚合的问题。
平衡理论:一个图中负边有偶数个,则图是平衡的,反之若负边为奇数个,则图是不平衡的。
地位理论:如果A和B有一条正向边连接,不仅意味着他们有正向关系,还意味着B的地位比A更高。反之,如果是负向边连接,意味着地位更低。
Motifs方法:首先根据平衡理论和地位理论的两个约束没去构建有向图白和无向图,2个定点和三个定点的所有可能性,并形成一个模板,每一个模板称为Motifs。如下图:
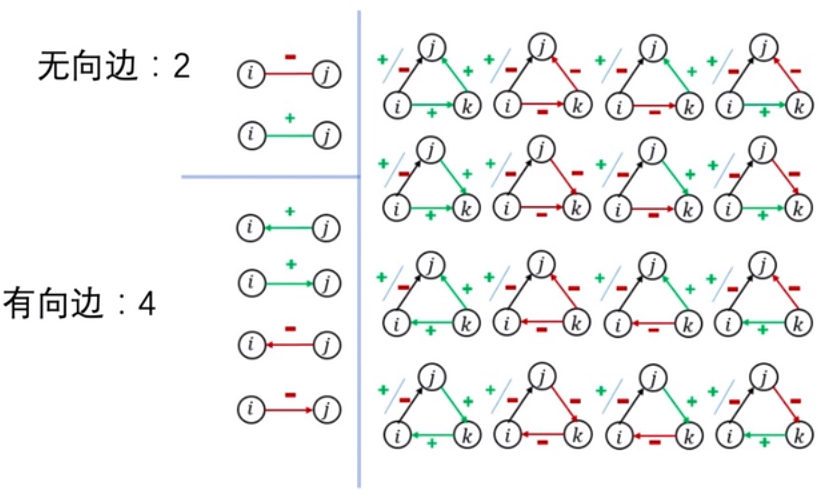
然后在SiGAT的使用过程中,对于每一个节点u,他会使用上图所示的每一种mofifs方法去寻找邻居(即图中的节点满足motifs模板的情况就认为是这种motifs的邻居)。然后找到邻居之后再每一种motifs下使用GAT的方式聚合邻居,再加上节点本身的特征拼接起来,再经过一个分类器,最终得到节点的表示特征。
SDGNN: Learning Node Representation for Signed Directed Networks
这个方法也利用了平衡理论和地位理论,只是并不像SiGAT中使用38个motifs,而是只使用有向边的4个motifs 进行邻居筛选,聚合方式也变成可以选择的方式,可以使用GAT进行聚合,也可以使用均值的方式进行聚合。然后这样的结构可以堆叠多层。
同时提出了三种损失函数
-
符号边:
对于u,v节点的边Lsign(u,v)=−yu,vlog(σ(zuTzv))−(1−yu,v)log(1−σ(zuTzv))
总的符号边损失函数为Lsign=∑eu,v∈E
-
地位理论:地位排序函数s(z)=sigmoid(W⋅z+b),s(zu)−s(zv)表示u,v之间的一个关系
然后可以得到一个损失函数Ldirection(u→v)=(quv−(s(zu)−s(zv)))2
其中quv={max(s(zu)−s(zv),γ),u→v:−min(s(zu)−s(zv),−γ),u→v:+,γ=0.5
最终地位损失函数为:Ldirection=∑eu,v∈ELdirection(u→v)
-
三角关系理论:
Jtri =∏Δ∈TJΔ
Ltriangle =−logJtri =∑Δ∈T−logJ△=∑Δ∈TL△
L△i,j,k=Lij+Lik+Lkj
Li,j=−yi,jlog(σ(zi⊤zj))−(1−yi,j)log(1−σ(zi⊤zj))
-
最终的Loss为:
Lloss =Lsign +λ1Ldirection +λ2Ltriangle ,
动态图
动态图相对于传统的图多了一个时间维度
动态网络表示可以按照时间粒度分为四个不同的级别:
- Static:不关注图中的动态信息,而将其作为一张静态图同等处理
- edge weight:动态信息只是作为一张静态图的节点或者边的labels而存在
- discrete:离散表示使用一组有序的图来表示动态图
- continuous network:使用确切时间信息的表示形式
离散表示(Discrete Representation):DG={G1,G2,...,G3},T表示快照数(有多少个时间间隔)
连续表示(Continuous Representation):可以分成三种表示方式
-
基于链接持续时间的动态网络的表示:
EB={(ui,vi,ti,Δi);i=1,2,...}
vi,vj表示发生事件的一对节点,ti发生事件,Δi持续时间
-
联系序列表示(瞬时发生,没有持续时间):
CS={(ui,vi,ti);i=1,2,...}
-
图流表示
GS={e1,e2,...},其中ei=(ui,vi,ti,δi),δi∈{−1,1}表示消失边和出现边
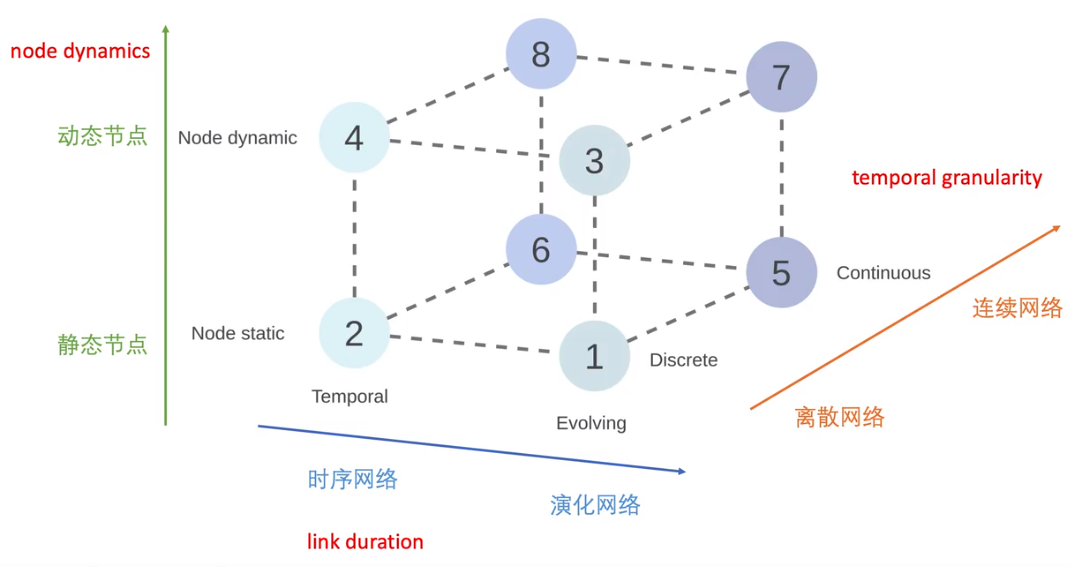
链接持续时间频谱:通过不同的持续时间可以分为四种网络
- Interaction networks:链接瞬时发生,发邮件
- Temporal networks:边有一定的持续时间,但比较短,人与人交谈
- Evolving networks:链接持续存在的时间比较长,雇佣关系
- Strictly evolving networks:链接出现后就会一直出现,比如引文网络
节点动态表示: 动态网络之间的另一个区别因素就是节点可能出现,也有可能消失
- Static:节点数量在一段时间内保持不变
- Dynamic:节点可能出现和消失
- Growing networks:只可能出现节点的网络
Dynamic Self-Attention Network(DySAT)
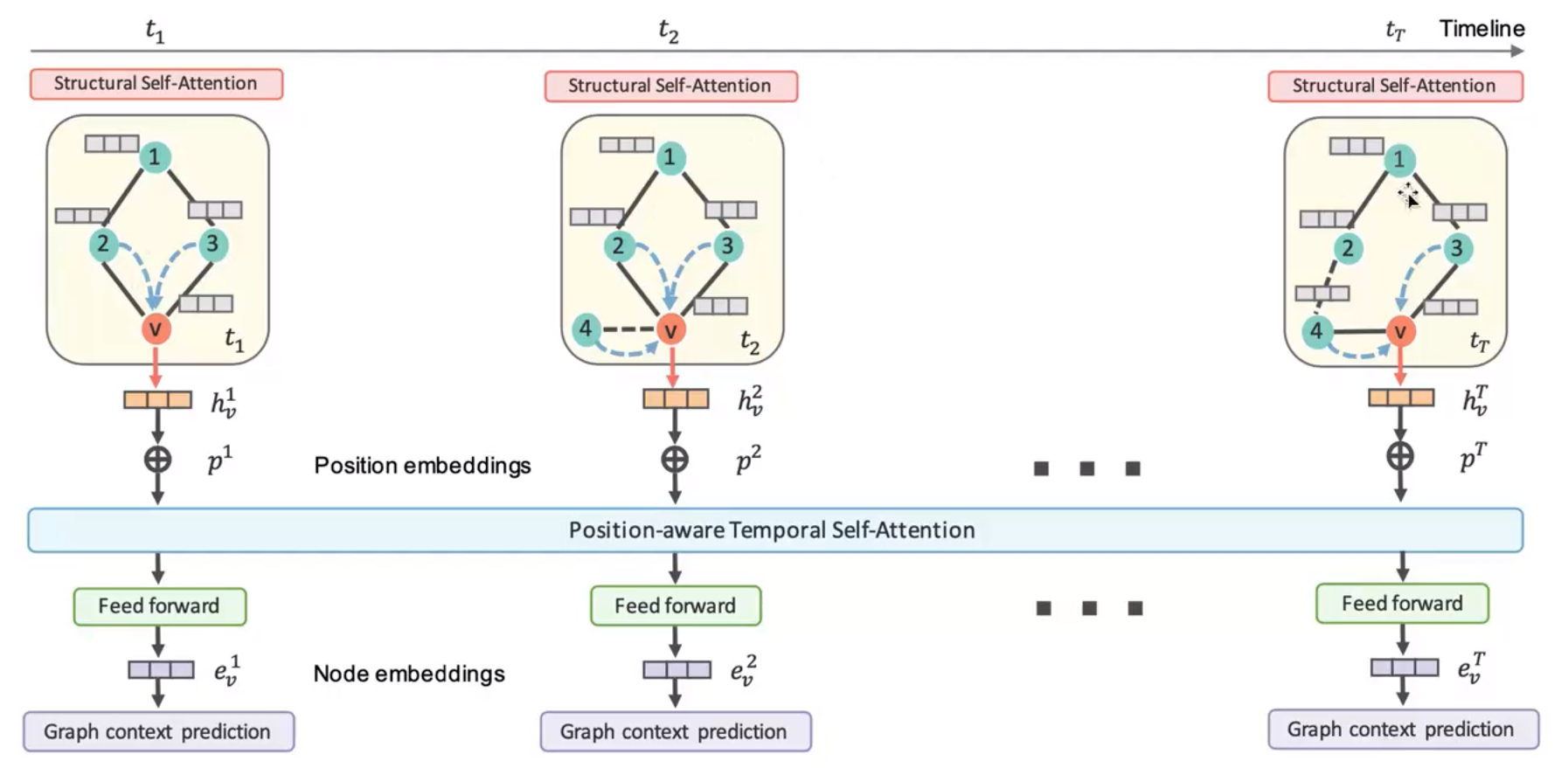
上图为DySAT的网络的结构。首先要了解这个算法的数据是怎么构建的,数据由时间,节点和边构成,描述了什么事件生成了什么节点和边,这时候就要根据自己定义的时间间隔去分离这些数据,然后按照分离的数据构造出上图所示的这些图结构。
然后在每一个图结构中计算节点的特征,如果没有特征就用one-hot表示。在图中针对任意一个节点v,其新表示是首先是计算其所有邻居对这个节点v的attention,计算方式是将两个节点加权乘积后拼接,使用一个α系数乘积,再乘上其边权,然后激活再softmax,最后得到邻居节点作用于这个节点的注意力,然后计算出每个邻居节点的注意力后将所有邻居节点乘上一个可学习权重,再乘上对应的注意力激活后,获得目标节点的新特征hvt。与GAT不同的是,多乘了一个边的权重。
在获得了每一个时刻图的新表示之后,加入一个要学习的位置embedding,然后采用self-attentioon的机制计算每个节点的emvedding。Wq,Wk,Wv分别是self-attention中的Q,K,V的权重,对于节点embedding Xv,将这个embedding分别乘以Q和K的权重得到的两个特征,在互相乘积使用一个缩放因子,然后考虑到当前图的时间,只作用之前的embedding,所以当前图的后面的图的就不用考虑,最后得到一个时间段Xv的权重evij,然后对这个表示使用softmax,得到QK计算出的注意力βvij,在使用V权重与Xv相乘,再与βvij的拼接结果βv相乘,得到最终的节点表示Zv
EvolveGCN:Evolving Graph Convolutional Networks for Dynamic Graphs
其核心公式主要有三个:
function[Ht(l+1),Wt(l)]=EGCU-O(At,Ht(l),Wt−1(l))Wt(l)=LSTM(Wt−1(l))Ht(l+1)=GCONV(At,Ht(l),Wt(l))
从这个结果中,从l层计算出l+1层的结果,首先是使用LSTM利用上一时刻t−1同一层的权重Wt−1(l)作为输入,生成当前时刻t的新的权重Wt(l)。然后将当前时刻的邻接矩阵At和这一层当前时刻的节点特征Htl,以及更新后的权重Wt(l)输入到图卷积中,计算下一层,当前时刻的特征Ht(l+1)
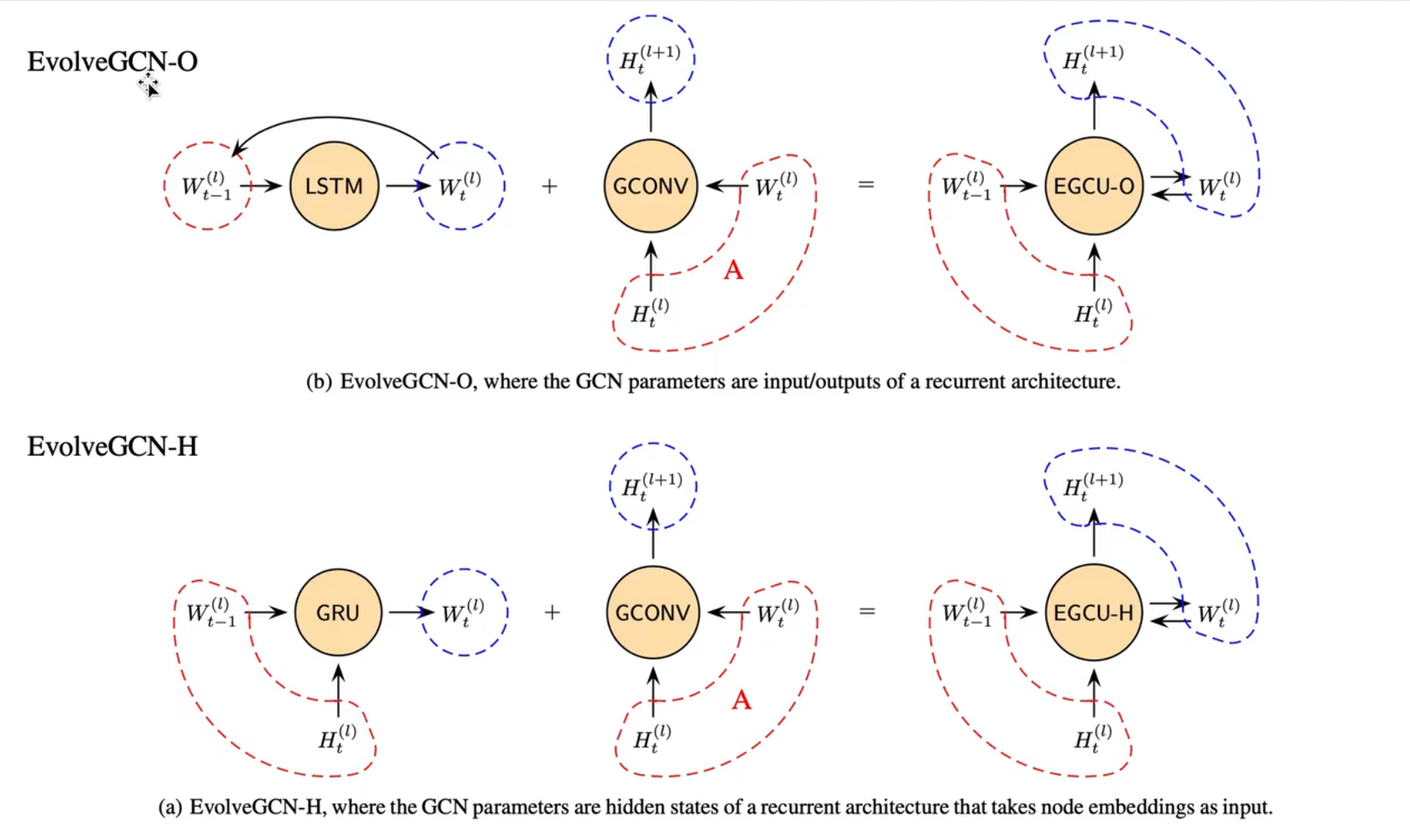
EvolveGCN-O就是上面三个公式描述的方法,对于EvolveGCN-H,他与EvolvGCN-O不同的地方在于,他除了使用权重对下一个权重进行更新外,还添加了当前时刻当前层的特征作为更新下一时刻权重的依据。用公式可以表示为:
function[Ht(l+1),Wt(l)]=PEGCU-H(At,Ht(l),Wt−1(l))Wt(l)=GRU(Ht(l),Wt−1(l))Ht(l+1)=GCONV(At,Ht(l),Wt(l))
两种方式的选择标准:
- 如果节点又信息,-H效果要好,因为考虑了节点的特征变化
- 如果节点信息比较少,-O效果好,因为他更新关系图结构的变化
Streaming Graph Neural Networks
主要解决的问题是:新的交互发生时,如何不断更新图网络的信息
当有新的节点交互产生时,应该更新交互的两个节点的特征,这个过程叫做更新组件。更新后的节点对其邻居也会产生一定的影响,也需要进行一定的更新,这个过程叫做传播组件。
更新组件
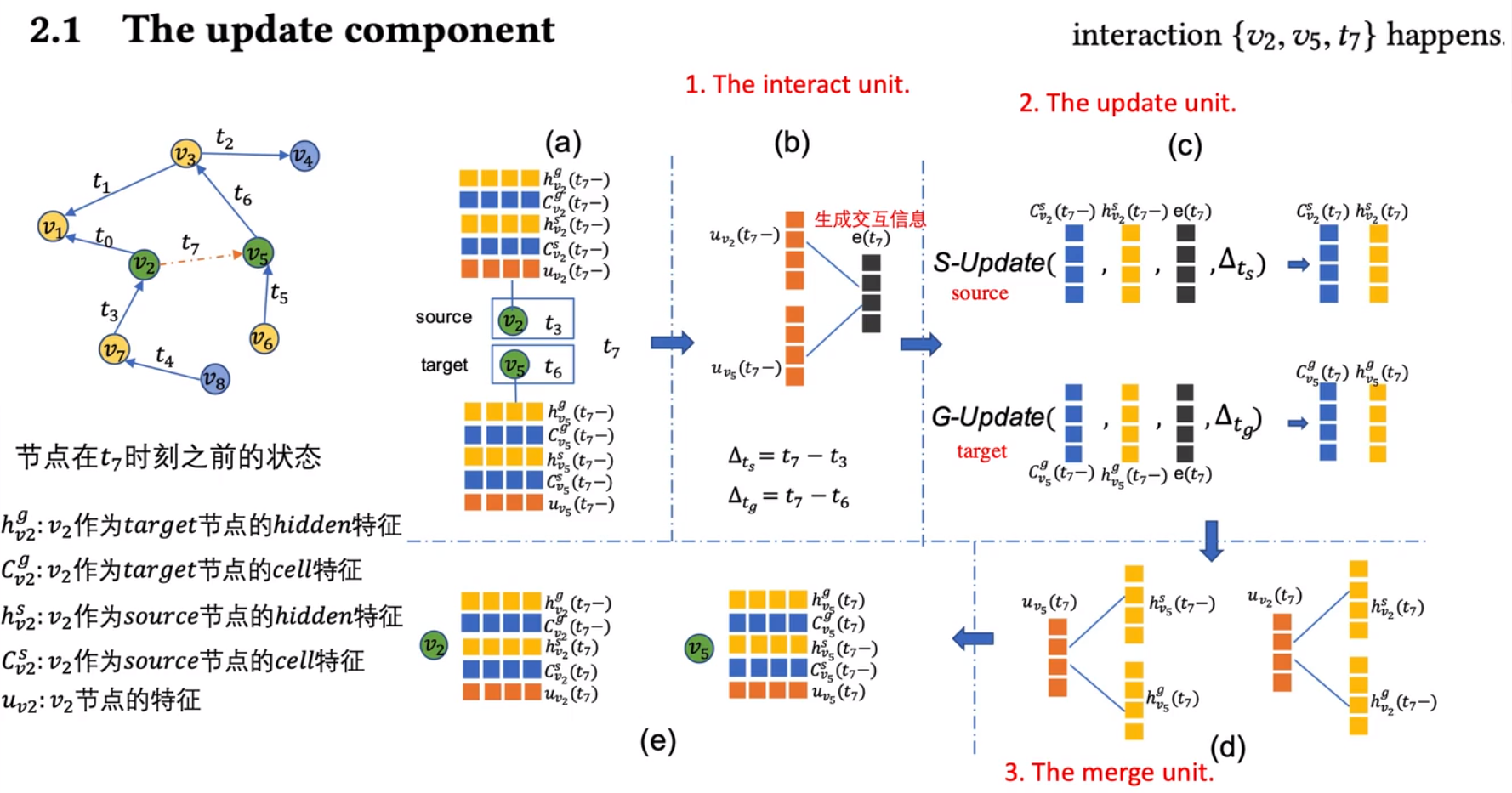
在某一时刻发生了source->target的一个交互(图中对应t7时刻v2->v5),在图中,v2是source,v5是target,所以v2只会更新source和节点特征,v5只会更新target和节点特征。uv2(t7−)表示的是t7时刻之前v2节点的特征。在interact unit中,对两个节点的特征u分别加权乘积加偏置激活得到交互信息e(t7),然后分别计算出时间间隔Δts和Δtg。
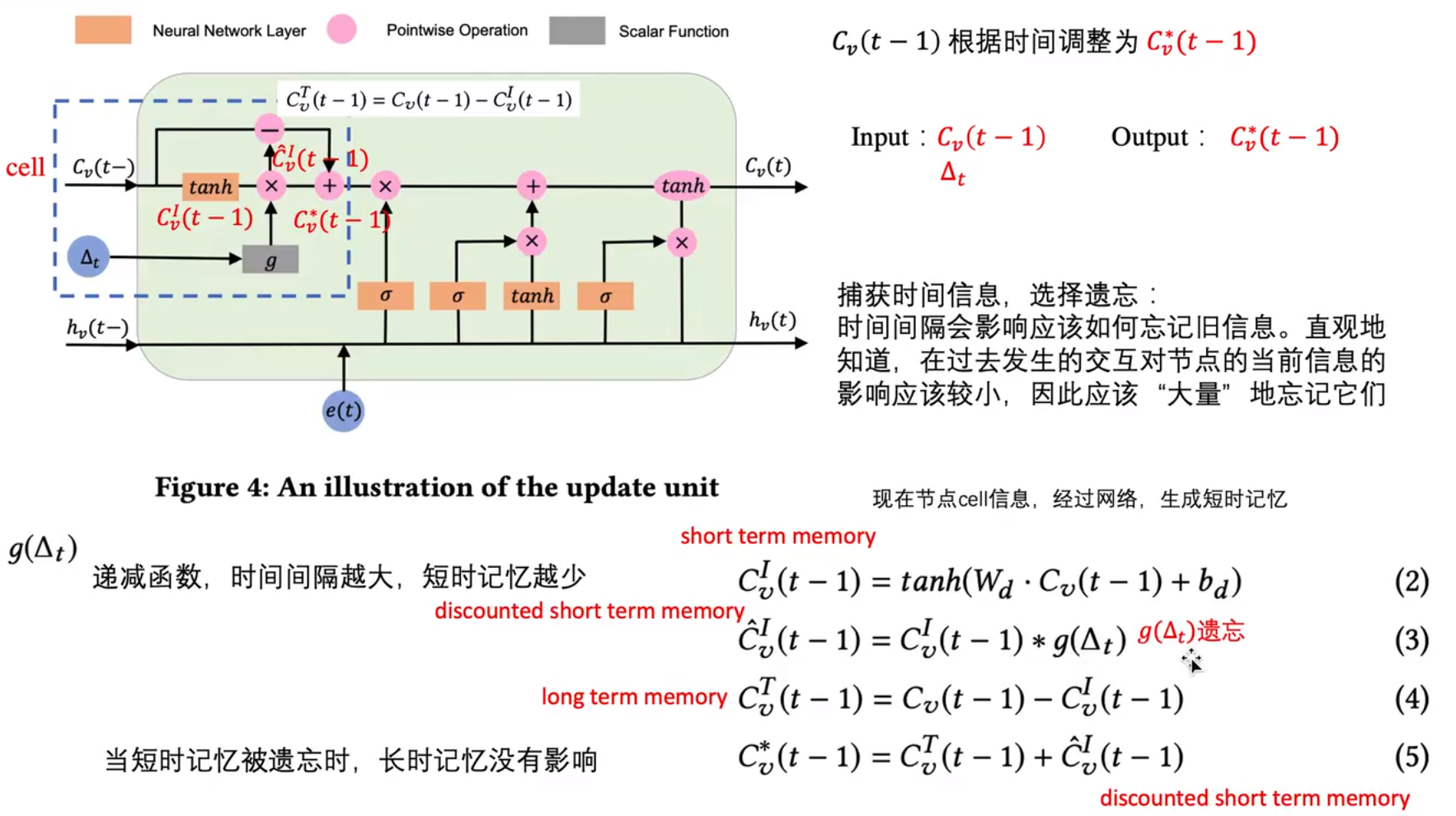
接着在update unite中分别使用S-Update和G-Update的操作更新target节点和source节点对应的特征。这两个更新操作的结构相同,但是参数不同。以S-Update为例,他的输入分别是Cv2s(t7−),hv2S(t7−),e(t7),ΔtS。其内部主要是一个LSTM结构,主要计算过程如下图所示:
接着在merge util中,对于source节点则是使用更新后的source特征和之前的target特征进行加权求和加偏置更新source节点的特征(这里的target特征使用的是t时刻之前的,是因为,在前面提到的source节点只更新source特征,target特征是不更新的)。同理target节点则是使用更新后的target特征和之前的source特征进行加权求和加偏置对target节点的特征进更新。
传播组件
在传播组件中,选择两个交互节点当前邻居作为受影响的节点。这组件的任务就是对受影响的节点进行更新。这样设置的原因如下:
- 新边缘对整个图的影响通常是局部的
- 在将信息传播到邻居之后,一旦受以你选哪个的节点与其他节点发生交互,信息将进一步传播
- 当传播更多的受影响点时,性能不会显著提高,甚至会降低,因为在传播过程中可能引入噪声。
在这个组件中,受影响节点如果是起始节点连接到交互的source节点时,那么这个节点叫做source节点影响邻居的source节点,同理,如果是终点就是source节点影响邻居的target节点。组件的结构图可以用下面的图表示:
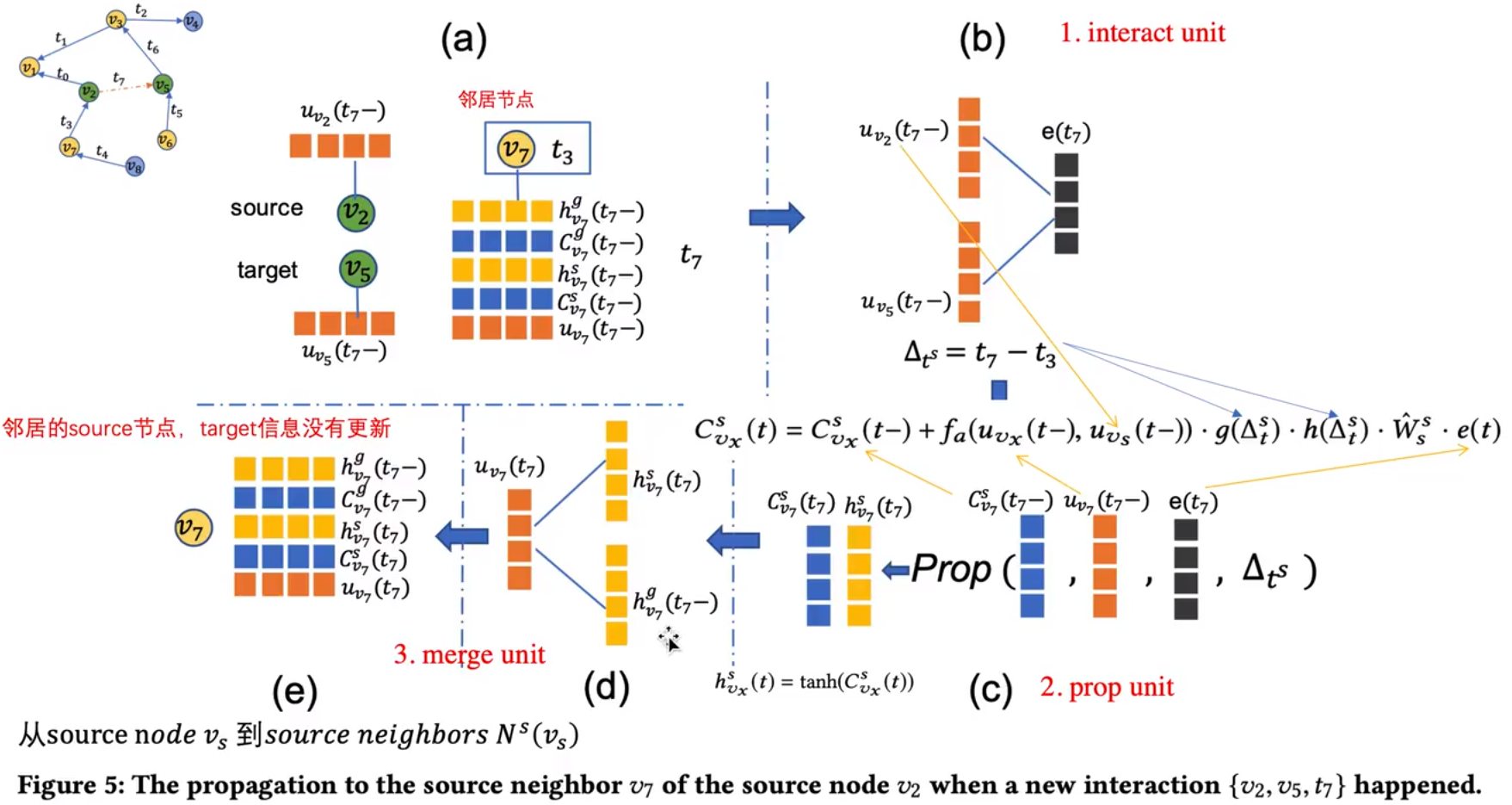
在prop unit中,CvxS(t−)表示的是受影响节点在t时刻之前的source特征,然后g(Δts)和之前一样,是控制时间间隔的一股函数,W^ss是可学习的权重,e(t)是interact unite输出的交互特征,h(Δts)={1,Δts≤τ0,otherwise,其含义是如果时间间隔超过τ就忽略他对受影响节点的影响。fa(uvx(t−),uvs(t−))=∑v∈Ns(vs)exp(uv(t−)T)uvs(t−)exp(uvx(t−)Tuvs(t−))
Temporal Graph Attention Network(TGAT)
TGAT与GAT相似,都是通过attention的方式去聚合节点的特征,此外,还考虑了节点的时间特征。对于一个节点的新特征Z,其在t时刻的计算公式为:
Z(t)=[h0l−1(t)∣∣Φdr(t−t),h1l−1(t1)∣∣Φdr(t−t1),...,hNl−1(tN)∣∣Φdr(t−tN)]T
h0l−1(t)是指节点0在上一层中时间为t的特征,然后t−tN表示的是一个时间差,Φd(t)=[cos(w1t+θ1),cos(w2t+θ2),...,cos(wdt+θd)]。除了第一个部分是节点本身,其他都是其邻居节点在上一层对应时刻的特征。
具体流程如下:
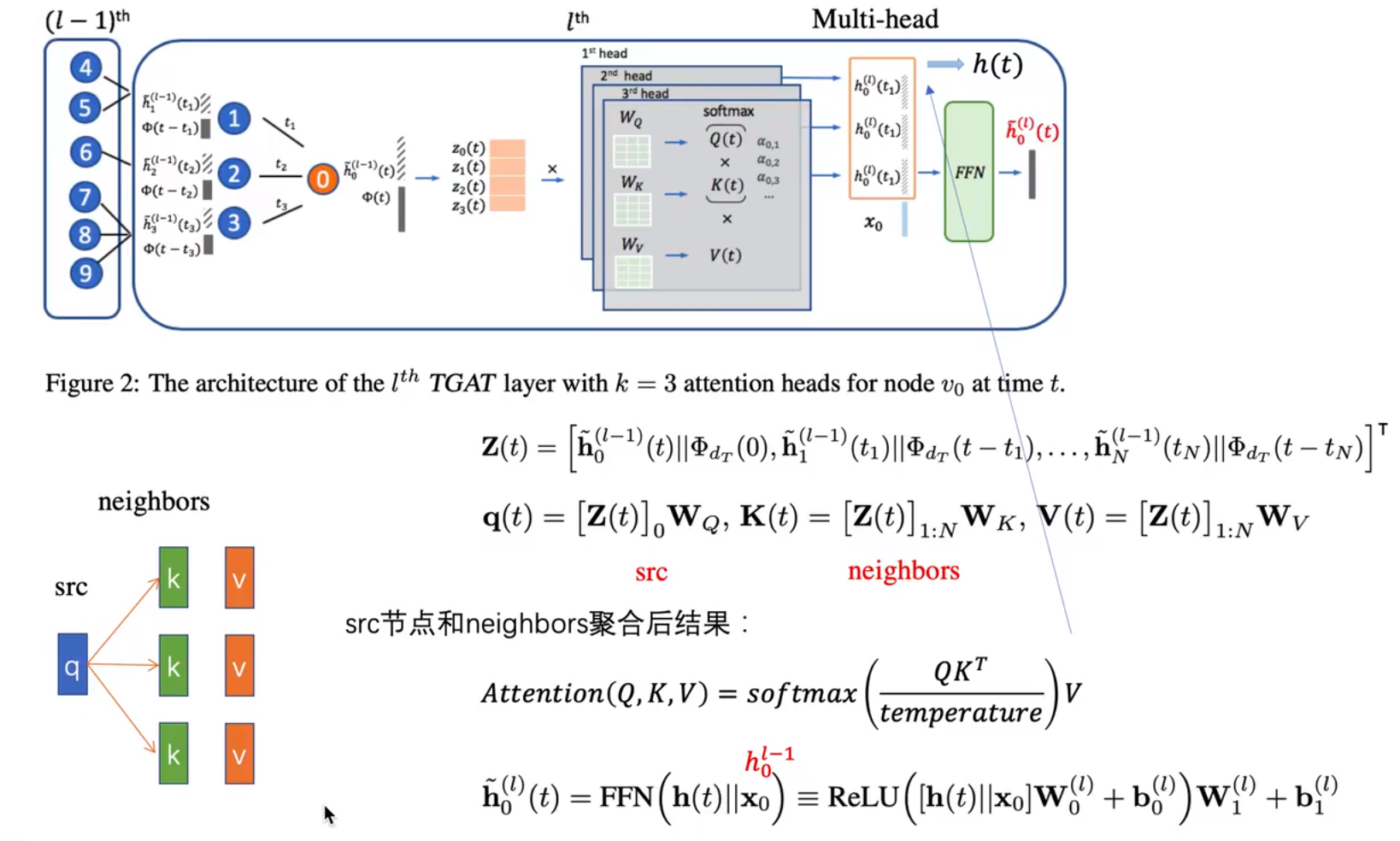
之前提到的特征Z对应图中橙色堆叠的部分,然后从图中可以看出,他是使用了一个多头的注意力进行计算(图中使用了3个头),在self-attention中有K,Q,V三个部分你,首选取出Z中的第0个特征(即目标节点加上时间特征的新表示)乘以Q的权重做为向量q,然后其邻居都乘上K的权重得到向量k,v则是其邻居都乘上V的权重,得到向量v。attention计算公式和图中一样。最后生成的头则是经过将这些头拼接起来,乘以一个权重+偏置+激活,再乘权重+偏置。
超图
超图是一种广义的关系结构,一个超边可以拥有任意数量的节点(>1),如果所有超编都链接两个节点那么超图就退化为简单图。
超图的定义G=(V,E,W),其中V是节点集合,E是超边集合,W是每个超边被赋予的权值。
超边的构建:
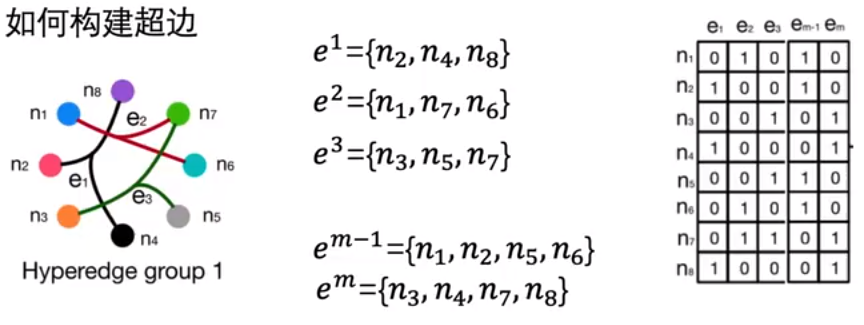
Hypergraph Neural Network(HGNN)
将GNN计算拓展到超图上,具体流程是图找培根能的公式10,加一个激活函数

Dynamic Hypergraph Neural Networks(DHGNN)
DHGNN的主要贡献是实现了GNN不同层之间动态地调整整层中的超图结构。
DHGNN主要有两个部分构成,一个是动态超图构建(DHG),另一个是超图卷积(HGC),算法总体结构如下图:
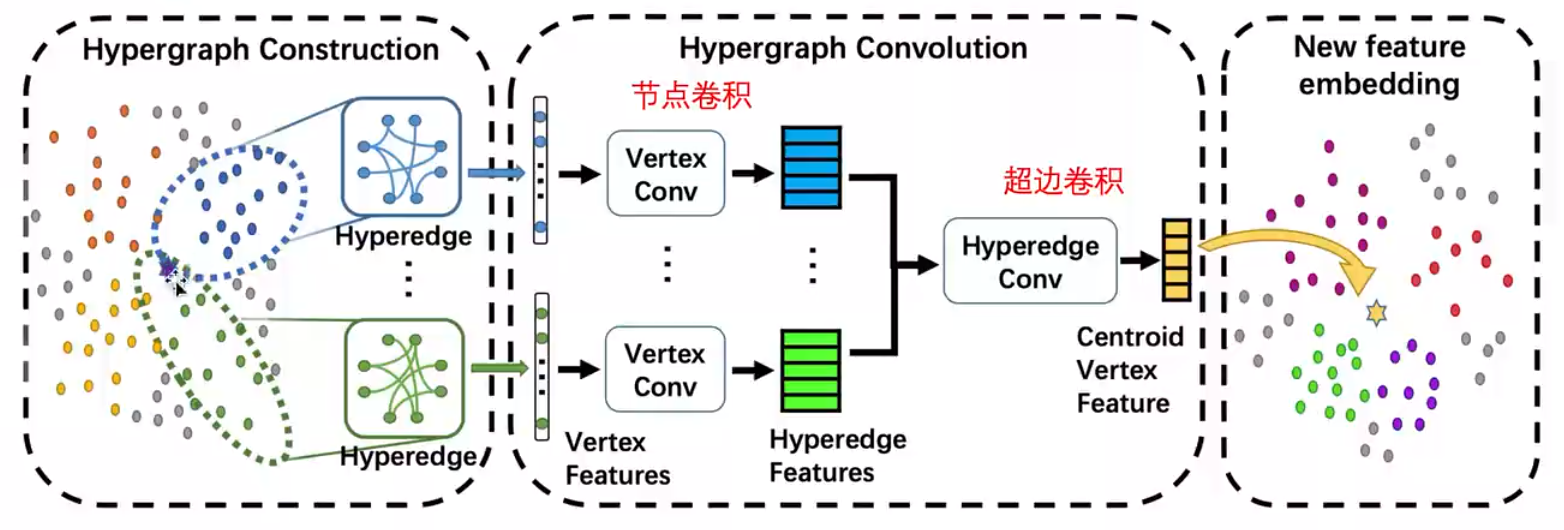
动态超图构建:主要使用KNN和K-means两种方式
输入:输入节点embedding X,KNN的参数k,K-Means簇的个数S
输出:超图集合G
- 使用K-means聚类X成C个类别
- 遍历X中的每一个节点
- 使用KNN计算该节点最近的k个节点
- 然后将这几个节点组成的超边加入到超图集合G中
- 然后计算当前节点与C各聚类中心的距离D
- 对D进行排序
- 取出前S-1个簇
- 遍历这S-1个簇
- 将当前簇中的所有节点与当前节点组成超边,然后加如到超图集合G中
- 结束遍历
- 结束遍历
- 输出超图集合G
超图卷积:也是有两个部分
- 顶点卷积将顶点特征聚集到超边
- 超边卷积将相邻的超边特征聚合到顶点
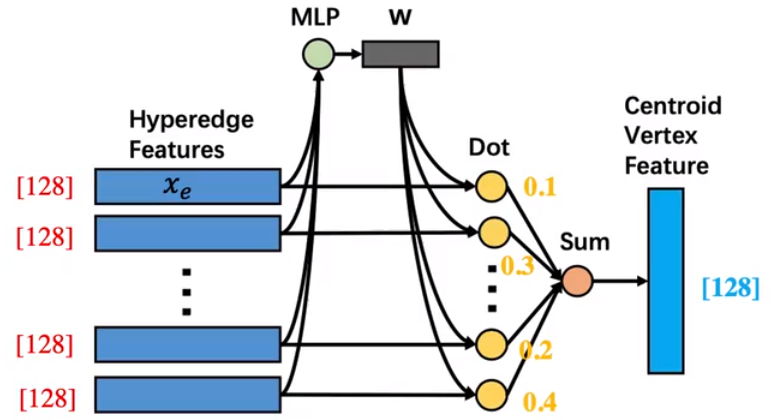
在顶点卷积中,会取出每一条超边(节点数 x 特征维度的一个矩阵结构),然后将其进行一个一维卷积转化,然后使用转化矩阵得到一个新的特征,然后在于原来的矩阵进行相乘,在经过一个一维卷积,转化为超边的特征。具体流程如下图:
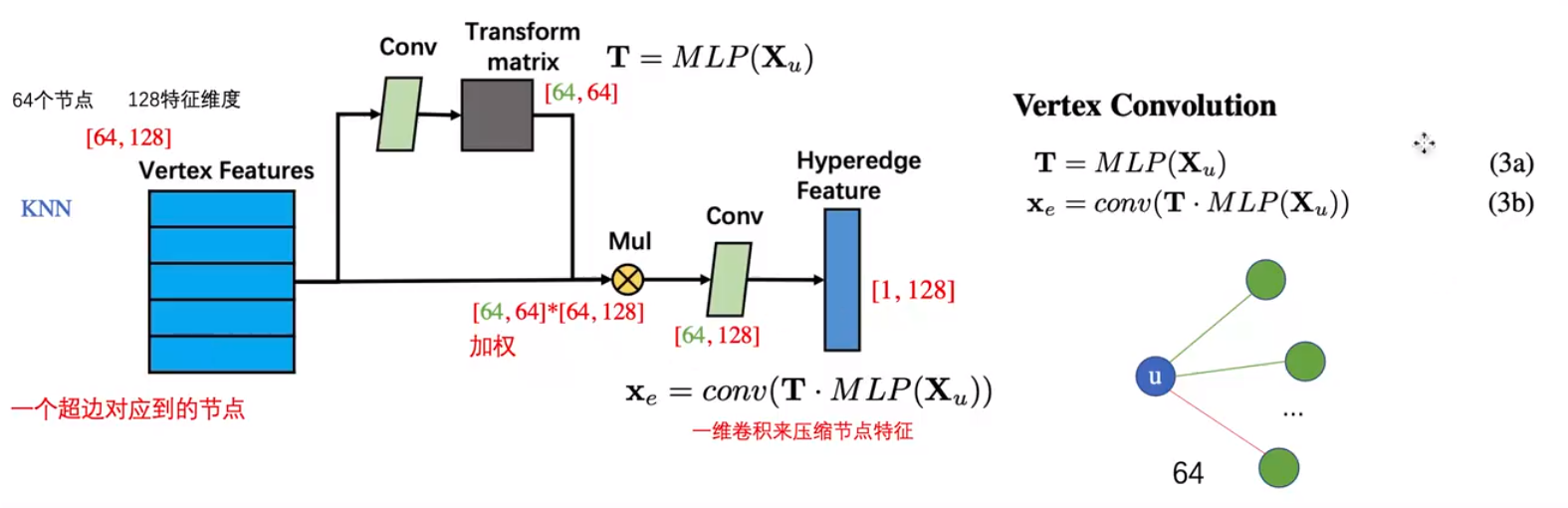
经过定点卷积会获得每一条超边的新表示Xe,然后使用这个超边特征经过一个MLP计算出这条超边的权重w=softmax(xeW+b),得到每一条超边的权重之后与对应的超边进行加权求和xu=∑i=0∣Adj(u)∣wixei得到节点对应的特征。