「论文阅读(简)」Policy-GNN: Aggregation Optimization for Graph Neural Networks

论文名称：Policy-GNN: Aggregation Optimization for Graph Neural Networks

作者：Kwei-Herng Lai, Daochen Zha, Kaixiong Zhou, Xia Hu

时间：2020

期刊或会议：KDD '20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining

代码：https://github.com/datamllab/Policy-GNN

原文摘要：

Graph data are pervasive in many real-world applications. Recently, increasing attention has been paid on graph neural networks (GNNs), which aim to model the local graph structures and capture the hierarchical patterns by aggregating the information from neighbors with stackable network modules. Motivated by the observation that different nodes often require different iterations of aggregation to fully capture the structural information, in this paper, we propose to explicitly sample diverse iterations of aggregation for different nodes to boost the performance of GNNs. It is a challenging task to develop an effective aggregation strategy for each node, given complex graphs and sparse features. Moreover, it is not straightforward to derive an efficient algorithm since we need to feed the sampled nodes into different number of network layers. To address the above challenges, we propose Policy-GNN, a meta policy framework that models the sampling procedure and message passing of GNNs into a combined learning process. Specifically, Policy-GNN uses a meta-policy to adaptively determine the number of aggregations for each node. The meta-policy is trained with deep reinforcement learning (RL) by exploiting the feedback from the model. We further introduce parameter sharing and a buffer mechanism to boost the training efficiency. Experimental results on three real-world benchmark datasets suggest that Policy-GNN significantly outperforms the state-of-the-art alternatives, showing the promise in aggregation optimization for GNNs.

理论基础

1. 不同的节点通常需要不同次数的聚合迭代去完全地捕获结构特征信息。
2. 图表征学习的目的提取图结构数据中的信息映射到一个低维的向量表示中。
3. GNN的研究主要有两个方向
   1. 提出采样策略去促进学习效率，然而采样策略可能造成信息损失从而得到一个次优的结果
   2. 新颖得消息传递方法被用于更好地捕获图结构中的信息。

任务与存在的问题

1. 给定一个复杂的图和稀疏的特征，为每一个节点探索一个有效的聚合策略是有挑战的
2. skip-connection可以使得GNN设计得更深，但他需要手动指定起始层和结束层构造skip-connection
3. 真实世界的图通常很复杂，具有多种类型的属性，很难为每个节点确定合适的聚合迭代
4. 即使我们可以为每一个节点定一个合适的聚合策略，但在这些节点上训练GNN仍然具有挑战性，因为我们需要将这些节点输入不同数量的网络层中。

主要的工作和创新点：

1. 对节点引入不同的聚合可以显著提高GNN的性能
2. 将GNN训练问题表述为一个MDP过程，并提出了一个使用强化学习来自适应优化聚合策略的元策略框架
3. 开发了一个基于DQN和GCN的框架实例，具有定制的奖励函数。并在三个真实世界的数据集上，本文提出的方法显著由于SOTA方案。

提出的方法

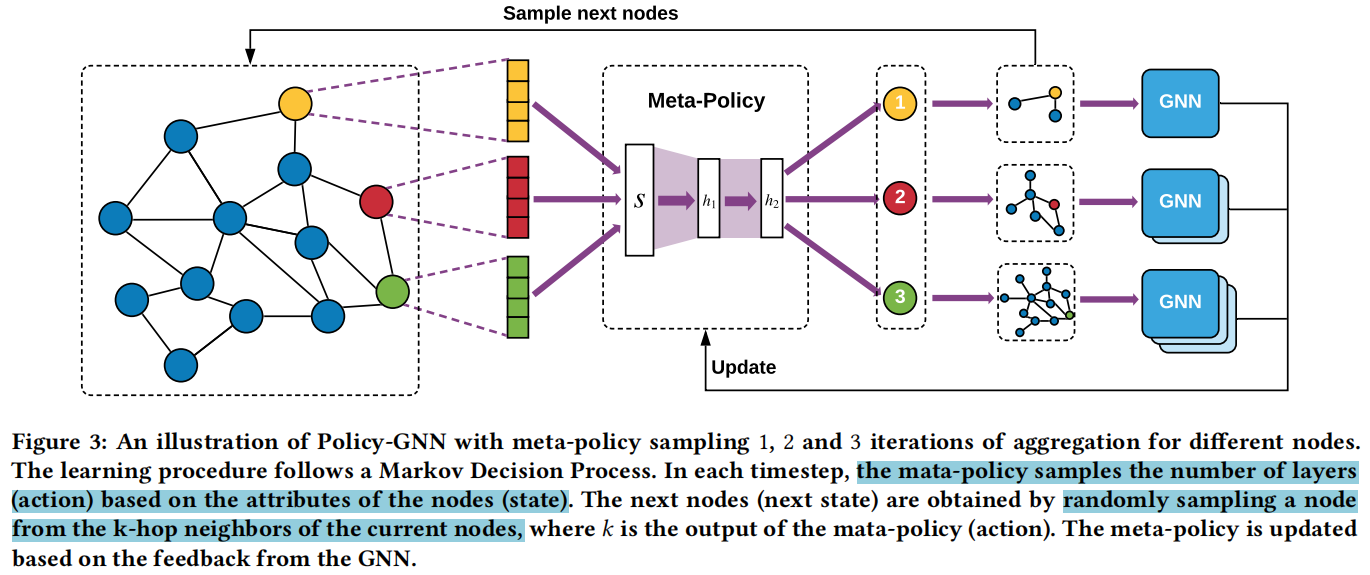
上图描述了方法的框架，由两个组件构成：Meta-Policy module 和 GNN module。前者的目的是学习节点特征和聚合迭代之间的关系，后者利用Meta-Policy来学习图表示。

Meta-Policy 将节点特征(红黄绿的特征向量)作为state，映射state得到action(跳数，红黄绿圈里的数字)，从每个节点的k-hops邻居中采样下一个状态（k是Meta-Policy的输出）。之后GNN module选择一个预先构建的k层GNN结构去学习一个节点的表征，得到一个reward signal并用于更新Meta-Policy。

使用深度强化学习进行聚合优化

MDP结构

1. State($\mathcal{S}$)：在第t个timestep的state $s_t\in\mathcal{S}$被定义为当前节点属性
2. Action($\mathcal{A}$)：在第t个timestep的action $a_t\in\mathcal{A}$具体来说就是当前节点的跳数(number of hops)
3. Reward Fucntion($\mathcal{R}$)：在第t个timestep的reward $r_t$作为特定任务与上一状态相比的性能提高。

基于上述的定义，聚合过程由三部分构成

1. 选择一个起始节点并得到他的属性作为当前的状态$s_t$
2. 从$\pi_{s_t}$中生成一个action $a_t$，以指定当前节点的跳数
3. 从$a_t$-hop邻居和他的属性中采样下一个节点作为下一个状态$s_{t+1}$

引导DQN的关键因素是reward signal，在reward函数中使用basline，其被定义为：

$$公式1：\mathcal{R}\left(s_{t}, a_{t}\right)=\lambda\left(\mathcal{M}\left(s_{t}, a_{t}\right)-\frac{\sum_{i=t-b}^{t-1} \mathcal{M}\left(s_{i}, a_{i}\right)}{b-1}\right),$$

其中$\frac{\sum_{i=t-b}^{t-1} \mathcal{M}\left(s_{i}, a_{i}\right)}{b-1}$是每一个timestep t 的baseline，$\mathcal{M}$是一个特定任务的评估度量，$b$是一个超参数，用于定义要为baseline引用的历史性能的窗口大小。$\lambda$是超参数，用于决定reward signal的强度，$\mathcal{M}(s_t,a_t)$是在第t个timestep中，在验证集上的任务表现。本文使用节点分类的准确率作为验证指标。

Policy-GNN算法

输入：最大层数K，DQN训练步数S，训练的epoch T，epsilon probability $\epsilon$，reward函数的窗口数$b$

初始化K层GNN，Q函数，memory buffer D，GNN buffer B

随机采样一个节点，使用其属性生成一个状态$s_0$

for t=0,1,2… do

1. 用概率$\epsilon$随机选择一个动作，否则得到$a_t=argmax_a\mathcal{Q}(s_t,a)$
2. 存储$s_t$和$a_t$到GNN buffer $B_{a_t}$中
3. 应用带有输入a和B的算法2(后面会写)来训练GNN
4. 使用公式3得到在测试集上的$r_t$
5. 从$a_t$-hop（第at跳的意思，与at-hops不太一样）采样下一个状态$s_{t+1}$
6. 存储三元组$T_t=(s_t,a_t,s_{t+1},r_t)$到D中
7. for step = 1,2,…,S do
8. 通过公式2使用数据D优化Qfunction

使用Meta-Policy进行图表征学习

GNN结构构建可以使用下面的方式表示

$$公式2\begin{array}{l} \mathbf{h}_{v}^{1}=\sigma\left(\sum_{u_{1} \in\{v\} \cup N_{1}(v)} \tilde{a}_{u_{1} v} \mathbf{W}_{1} \mathbf{X}_{u}\right), \\ \vdots \\ \mathbf{h}_{v}^{k=a_{t}}=\sigma\left(\sum_{u_{k} \in\left\{u_{k-1}\right\} \cup N_{k}(v)} \tilde{a}_{u_{k} u_{k-1}} \mathbf{W}_{k} \mathbf{h}_{v}^{k-1}\right), \\ \text { output }=\operatorname{softmax}\left(\mathbf{h}_{v}^{a_{t}}\right), \end{array}$$

其中$\mathbf{h}_v^k$是节点v在第k层的d维的特征向量，$\mathbf{X}_u$是节点u的输入特征向量，$\mathbf{W}_k$是第k层可训练的参数，$\sigma$是每一层的激活函数，$k=a_t$是通过$\widetilde{\pi}$在第t个timestep决定的聚合数。

使用Buffer机制和参数共享加速Policy-GNN

参数共享：本文通过使用参数共享机制减少训练的参数量。具体来说，本文首先初始化GNN的最大层数(k)，然后在每一个timestep，通过初始化的顺序堆叠各层，以便对action $a_t$执行GNN训练。通过这种方式，如果每一层的隐藏单元数是n，可以只需要训练$k\times n$的参数，而不是$\frac{nk(k+1)}2$的参数

用于图表征学习的Buffer机制：本文为每一个可能的action构建buffer。在每一个timestep中，在得到一个batch的节点属性和一个batch的action之后，本文存储他们到action buffer中，并检查buffer是否达到了batch size。如果一个特定的action的buffer是满的，那么我们使用选择的layers构建GNN，并用action buffer中的数据训练GNN。再GNN上训练完数据后，再将buffer中的数据清楚。实际上，如果batch处理大小太大，该机制仍然需要很多时间，然而，与只有一个训练实例在每个timestep中costly的GNN构建相比，该机制显著提高了训练效率。

使用Buffer机制训练GNN的算法

输入：动作$a$，GNN buffer $\mathcal{B}$

1. if $\mathcal{B}_a$是满的 then
2. for layers = 1,2,… a do
   1. 向上一节中提到的一样堆叠GNN层数
3. end for
4. 在action buffer $\mathcal{B}_a$上训练堆叠的GNN
5. 清空buffer $\mathcal{B}_a$
6. end if

首先初始化K个GNN层，Q函数，GNN buffer $\mathcal{B}$和memory buffer $\mathcal{D}$去存储经验。然后，随机地采样一个batch的节点并使用节点的属性生成第一个状态。将state输入到Q函数中，得到带有$\epsilon$概率的actions，再通过随机选择动作。基于选择的动作，本文按顺序从初始的GNN层中堆叠层数。在验证集上训练选择的层来得到反馈。通过对验证集的反馈，通过公式1进一步得到reward signal，并将transitions存储到memory buffer中。通过这种方式，根据过去在memory buffer的经验，从memory buffer中随机抽取成批的数据，并根据下面的公式进行优化，并进行下一次迭代：

$$公式3：Q(s, a)=\mathbb{E}_{s^{\prime}}\left[\mathcal{R}\left(s^{\prime}\right)+\gamma \max _{a^{\prime}}\left(Q\left(s^{\prime}, a^{\prime}\right)\right]\right.$$