「论文阅读」Graph Policy Network for Transferable Active Learning on Graphs

论文名称： Graph Policy Network for Transferable Active Learning on Graphs

作者：Shengding Hu, Zheng Xiong, Meng Qu, Xingdi Yuan, Marc-Alexandre Côté, Zhiyuan Liu, Jian Tang

期刊或会议：NeurIPS 2020

时间：2020-7

代码：ShengdingHu/GraphPolicyNetworkActiveLearning

原文摘要

Graph neural networks (GNNs) have been attracting increasing popularity due to their simplicity and effectiveness in a variety of fifields. However, a large number of labeled data is generally required to train these networks, which could be very expensive to obtain in some domains. In this paper, we study active learning for GNNs, i.e., how to effificiently label the nodes on a graph to reduce the annotation cost of training GNNs. We formulate the problem as a sequential decision process on graphs and train a GNN-based policy network with reinforcement learning to learn the optimal query strategy. By jointly training on several source graphs with full labels, we learn a transferable active learning policy which can directly generalize to unlabeled target graphs. Experimental results on multiple datasets from different domains prove the effectiveness of the learned policy in promoting active learning performance in both settings of transferring between graphs in the same domain and across different domains.

任务与存在的问题

训练图表征通常需要大量的标记数据，然而这在一些领域(化学和医疗保健领域)中获取这样大量的标签数据是非常昂贵的。

在每一步查询中根据选择标准标记最具有信息的节点这种方法存在两个问题：

1. 忽视了长期(long-term)表现
2. 缺乏节点之间的交互

主要的工作和创新点

针对如何有效地标记图中节点的标签，减少训练GNN的标记开销问题，本文将其描述为在图上的序列选择过程，使用强化学习的方式训练一个基于GNN的策略网络，去学习最佳的查询策略。通过对几个具有完整标签的源图进行联合训练，学习了一个可转移的主动学习策略(transferable activate learning policy)，他可以直接推广到未标记的目标图上。

1. state：基于当前图的状态进行定义
2. action：在每一步查询中选择一个节点去标记
3. reward：所选节点训练GNN的性能增益

提出的方法

问题描述

图$G=(V, E)$,$V$是节点集合,$E$是边集，每一个节点$v \in V$对应一个特征向量$x_v \in \mathcal{X} \subseteq \mathbb{R}^d$，还有一个标签$y_v \in \mathcal{Y}=\{1,2, \cdots, C\}$，节点集合被分为三个自己，分别是$V_{\text {train }}, V_{\text {valid }}$和$V_{\text {test}}$。在传统的半监督节点分类任务中，给定一个子集的标签$V_{label}\subseteq V_{\text {train }}$，学习利用图G和$V_{label}$的分类网络$f_{G,V_{label}}$(GNN模型)，对$V_{test}$中的所有节点进行分类。

对于在图上的activate learning，初始化训练的子集为一个空集，$V_{label}^0=\empty$，给定一个query budget $B$，其允许我们从$V_{train}$中依次获取B样本的标签，其中$B \ll\left|V_{\text {train }}\right|$，在每一步$t$中，我们根据主动学习策略$\pi$从$V_{\text {train }} \backslash V_{\text {label }}^{t-1}$中选择一个未标记的节点$v_t$，并查询$v_t$的标签，接下来，将标记的节点集合更新为$V_{\text {label }}^t=V_{\text {bbel }}^{t-1} \cup\left\{v_t\right\}$。接着使用更新的$V_{label}^t$来训练分类GNN $f$。当budget $B$用完时，我们停止查询过程，继续使用$V_{label}^B$训练GNN $f$直到收敛

我们使用强化学习在多个标记的训练图上学习activate learning policy $\pi$，并在没有微调和冲洗你训练策略的情况下，评估初始无标记测试图上的学习策略，即zero-shot policy transfer.

在训练阶段，我们收集一组带有节点标签的源图$G_{\mathcal{S}}$，学习最优策略$\pi^*$最大化$\sum_{G \in \mathcal{G}_S} \mathcal{M}\left(f_{G, V_{label}^B}\right)$。其中$\mathcal{M}(\cdot)$是一个指标用于验证分类GNN的表现。$V_{1abel}^B=\left(v_1, \ldots, v_B\right)$是在图$G$上，基于budget $B$标注并被$\pi^*$标记的节点序列。

在验证阶段，我们将学习到的策略$\pi^*$直接应用与一组目标图$\mathcal{G}_T$，对于每一个$G \in \mathcal{G}_T$，我们最初没有节点标签，然后选择一个节点序列基于$\pi^*$进行标记，然后使用他们在$G$上训练分类GNN。我们最终的目标是从$\mathcal{G}_S$学习可转化的active learning policy $\pi^*$，他可以在$\mathcal{G}_T$上表现良好，而不需要微调或再训练。

在图上的 activate learning可以看成一个MDP

State

我们定义在图G上第t步的状态为一个矩阵$S_G^t$，其中每一行$S_v^t$是节点$v$的状态表示，我们根据active learning中几个常用的启发式标准来定义每一个节点的状态。

• 计算节点的度数来衡量节点的表示性，从直觉上看，高度数的节点可能是图中的枢纽，因此他们的标签很可能更有信息性。为了保证计算的稳定性，我们使用一个超参数$\alpha$来缩放节点的度数，并将其clip为1：

  $$公式1：\mathbf{s}_v^t(1)=\min (\text { degree }(v) / \alpha, 1)$$

• 我们计算标签和分类GNN $f$在每个节点上的预测分布的熵来衡量他的不确定性。如果网络对其在某些节点上的预测没有信心，那么这些节点的标签很可能更有用。我们将熵除以$log(\#classes)$，以适应其在$[0,1]$的范围之内，这确保了他在图间的transferablility，即使有不同的类别数量

  $$公式2：\mathbf{s}_v^t(2)=H(\bar{y}(v ; t)) / \log (\#classes)$$

  其中$\bar{y}(v ; t) \in \mathbb{R}^C$是通过分类GNN在第t步预测的节点$v$的类别概率

• 除了节点本身的熵以外，我们也关注节点和他们邻居预测标签分布之间的散度，邻居节点直接散度衡量局部图的相似性，这可以帮助active learning policy更好地辨别图中的潜在的聚类和决策边界。本文将节点$v$和他的邻居$N_v$预测的标签分布之间的平均KL散度和反转KL散度，作为局部相似性的度量。

  $$公式3：\mathbf{s}_v^t(3)=\frac{1}{\left|N_v\right|} \sum_{u \in N_v} \operatorname{KL}(\bar{y}(v ; t) \| \bar{y}(u ; t)), \mathbf{s}_v^t(4)=\frac{1}{\left|N_v\right|} \sum_{u \in N_v} \operatorname{KL}(\bar{y}(u ; t) \| \bar{y}(v ; t)) .$$

• 我们使用一个指标变量去表示一个节点是否被标记

  $$公式4：\mathbf{s}_v^t(5)=\mathbb{1}\left\{v \in V_{\text {label }}^{t-1}\right\} .$$

我们拼接这些特征去形成每一个节点$s_v^t$的状态表征，总的来说，我们可以容易地加入其他启发式的特征到这个灵活的框架中，通过添加他们到节点的表示向量中。然而，我们只使用5个基本的特征，并利用策略网络自动地学习更复杂，信息更丰富的节点选择标准(selection criterion)。图状态矩阵$S_G^t$将传递到策略网络$\pi$中生成动作可能性。

Action

在第t步中，action是从基于$p_G^t \sim \pi\left(\cdot \mid S_G^t\right)$的$V_{\text {train }} \backslash V_{\text {label }}^{t-1}$选择的节点$v_t$，通过第t步的策略网络给定动作可能性。

Reward

我们使用分类GNN在收敛后验证集上的性能分数作为一个trajectory的rewad。然而这个trajectory reward与使用step-wise performance gain作为即时奖励，是延迟和稀疏的。他提供了一个更加稳定的策略质量估计，因为他在分类GNN的训练过程中对随机干扰因子具有更强的鲁棒性。给定一个标记节点的序列$V_{\text {label }}^B=\left(v_1, \ldots, v_B\right)$，我们定义trajectory reward为

$$公式5：R\left(V_{\text {label }}^B\right)=\mathcal{M}\left(f_{G, V_{\text {label }}^B}\left(V_{\text {valid }}\right), y_{\text {valid }}\right)$$

其中$f_{G, V_{\text {label }}^B}$是使用图$G$和标签$V_{label}^B$训练的分类GNN，$V_{valid}$和$y_{valid}$是验证集的节点和标签，$\mathcal{M}$是评估指标。

State Transition Dynamics

在每一个查询步骤t中，一个新的标记节点$v_t$被添加到$V_{label}^t$中，并用于更新分类GNN。图的state也由$S_G^t$转移到$S_{G+1}^t$。具体来说，在被选择的节点$v_t$的状态向量中，选择指标被从0修改到1.更新分类GNN会影响预测标签分布，因此在每个节点的状态向量中，熵和KL散度项将被相应地改变。因为直接建模transition dynamics $p\left(S_G^{t+1} \mid S_G^t, v_t\right)$是困难的，因此我们用model-free的方法学习最优的策略。

Framework

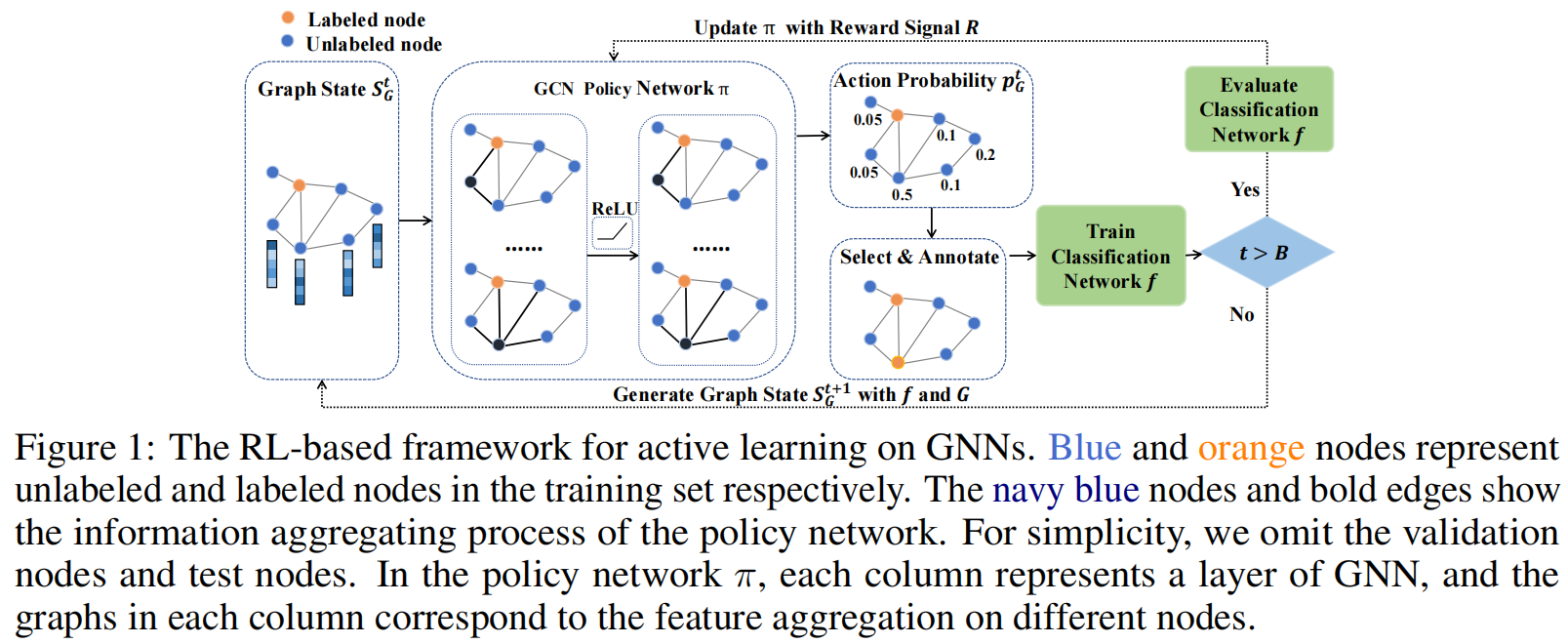
在每一个查询步t中，我们首先使用图$G$和分类GNN $f_{G, V_{\text {lakel }}^{t-1}}$的输出更新当前图状态$S_G^t$。策略网络$\pi$使用$S_G^t$作为输入，生成一个覆盖动作的概率分布$p^t_G$，其表示在候选池$V_{\text {train }} \backslash V_{\text {label }}^{t-1}$标签中对每个未标记节点进行注释的概率。接下来，我们基于$p_G^t$采样一个节点$v_t$用于标注，并添加他到已标记的训练子集中得到$V_{label}^t$。使用$V_{label}^t$训练分类GNN $f$，然后使用他去生成下一步的图状态$S_G^{t+1}$。当$t=B$时，我们停止查询阶段，并训练$f$直到其收敛。 最后，我们在测试集$V_{valid}$上验证 $f_{G,V_{label}^B}$，performance score被当做trajectory reward R去更新策略网络$\pi$

策略网络结构

基于图的拓扑结构，在图上的active learning的关键特征是每个节点彼此之间都是高度关联的。这为在不同的查询步骤中的每个候选节点的信息量提供了有价值的信息。我们使用GNN参数化策略网络$\pi$，其交互聚合邻居信息去更每一个节点的状态表征。具体来说，我们使用L层的GCN去实现策略网络，GCN的第l层的传播规则如下：

$$公式6：H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right),$$

其中$W^{(l)}$和$H^{(l)}$分别是第l层的权重和输入特征。$\tilde{A}=A+I$是具有自环的邻接矩阵，$\tilde{D}$是对角矩阵，其中$\tilde{D}_{i i}=\sum_i \tilde{A}_{i j}$。我们使用ReLU作为激活函数$\sigma$，在第一层中，$H^{(0)}=S_G^t$

在GCN的顶层，我们使用线性层(输出为1)去最后输出embedding $H^{(L)}$，得到每个节点的real number score。这个分数通过softmax生成覆盖所有候选节点$V_{\text {train }} / V_{\text {label }}^{t-1}$的概率分布$p_G^t$：

$$公式7：p_G^t=\pi\left(\cdot \mid S_G^t\right)=\operatorname{Softmax}\left(W H^{(L)}+b\right)$$

策略训练

在训练阶段，给定一组$N_S$个标记的源图$\mathcal{G}_S=\left\{G_i \mid i=1, \ldots, N_S\right\}$，我们的目标是最大化从以下策略$\pi$在训练图上获得的期望奖励的总和。包含策略网络参数$\theta$目标函数可以被定义为：

$$公式8：J(\theta)=\sum_{i=1}^{N_S} \mathbb{E}_{P\left(V_{\text {labkl }}^{B_i}=\left(v_1, \ldots, v_{B_i}\right) ; \theta\right)}\left[R_i\left(V_{\text {label }}^{B_i}\right)\right]$$

其中$B_i$是在图$G_i$ 上的query budget，$R_i$是图G上的trajectory rewad。我们使用$REINFORCE$策略梯度方法去训练策略网络。对于多源图上的联合训练，我们迭代每一集合中的所有训练图来更新策略网络。因为不同的查询序列将在策略训练中进行尝试，我们需要在这些训练图上的full label information。

策略转化和验证

在验证阶段，给定一组$N_T$个无标记的目标图$\mathcal{G}_T=\left\{G_i \mid i=1, \ldots, N_T\right\}$，我们直接在每一个测试图上应用学习策略$\pi_{\theta}$去执行active learning

具体来说，在每一测试图$G \in \mathcal{G}_T$，我们初始化每一个节点都不含标签。在每一个查询步t中，我们首先计算每一个节点的状态向量并得到图G状态矩阵$S_G^t$。然后状态矩阵传递到策略网络$\pi$中，计算动作概率。其中策略参数$\theta=\left\{W^{(0)}, \ldots, W^{(L)}, W, b\right\}$直接从训练阶段复制，而图图谱矩阵$\tilde{D},\tilde{A}$被测试图的进行代替。我们通过最大动作概率选择候选节点进行标记，并添加他到标记训练集中去更新分类网络。更新的分类网络的预测结果被用于去生成下一个查询步的状态矩阵。我们重复删除的步骤直到达到query budget，最后训练分类网络直到收敛。