论文:View-Consistency Learning for Incomplete Multiview Clustering
作者:Ziyu Lv ; Quanxue Gao ; Xiangdong Zhang ; Qin Li ; Ming Yang
期刊:IEEE Transactions on Image Processing
时间:2022-7
原文摘要
In this article, we present a novel general framework for incomplete multi-view clustering by integrating graph learning and spectral clustering. In our model, a tensor low-rank constraint are introduced to learn a stable low-dimensional representation, which encodes the complementary information and takes into account the cluster structure between different views. A corresponding algorithm associated with augmented Lagrangian multipliers is established. In particular, tensor Schatten p -norm is used as a tighter approximation to the tensor rank function. Besides, both consistency and specificity are jointly exploited for subspace representation learning. Extensive experiments on benchmark datasets demonstrate that our model outperforms several baseline methods in incomplete multi-view clustering.
理论基础
不同视图的数据可以提供更有用的互补和辨别信息,这对提高算法的鲁棒性非常有帮助。
现有的不完整多视图聚类方法可以分为两类:基于矩阵分解的不完整多视图聚类(MFIMC),基于图的不完整多视图聚类(GIMC)
符号说明
符号
说明
Z ∈ R n 1 × n 2 × n 3 \mathbf{\mathcal{Z}} \in \mathbb{R}^{n_1 \times n_2 \times n_3} Z ∈ R n 1 × n 2 × n 3 加粗的字母表示三阶的张量
Z \mathbf{Z} Z 加粗大写字母表示矩阵
z \mathbf{z} z 加粗小写字母表示向量
z i j k z_{ijk} z ijk 小写字母表示Z \mathbf{\mathcal{Z}} Z
Z ( i ) \mathcal{Z}^{(i)} Z ( i ) 表示在第一维度的第i个项
Z ‾ = fft ( Z , [ ] , 3 ) \overline{\mathcal{Z}}=\operatorname{fft}(\mathcal{Z},[], 3) Z = fft ( Z , [ ] , 3 ) Z ‾ \overline{\mathcal{Z}} Z
t r ( Z ) tr(\mathbf{Z}) t r ( Z ) 表示矩阵Z \mathbf{Z} Z
$
定义1 :t-乘法,给定X ∈ R n 1 × m × n 3 \mathcal{X} \in \mathbb{R}^{n_1 \times m \times n_3} X ∈ R n 1 × m × n 3 Y ∈ R m × n 2 × n 3 \mathcal{Y} \in \mathbb{R}^{m \times n_2 \times n_3} Y ∈ R m × n 2 × n 3 X ∗ Y ∈ R n 1 × n 2 × n 3 \mathcal{X} * \mathcal{Y} \in \mathbb{R}^{n_1 \times n_2 \times n_3} X ∗ Y ∈ R n 1 × n 2 × n 3
公式 1 : X ∗ Y = ifft ( bdiag ( X Y ‾ ) , [ ] , 3 ) , 公式1:\mathcal{X} * \mathcal{Y}=\operatorname{ifft}(\operatorname{bdiag}(\overline{X Y}),[], 3),
公式 1 : X ∗ Y = ifft ( bdiag ( X Y ) , [ ] , 3 ) ,
其中,X ˉ = bdiag ( X ‾ ) \bar{X}=\operatorname{bdiag}(\overline{\mathcal{X}}) X ˉ = bdiag ( X ) X ‾ \overline{\mathcal{X}} X
定义2 :t-SVD,Z ∈ R n 1 × n 2 × n 3 \mathcal{Z} \in \mathbb{R}^{n_1 \times n_2 \times n_3} Z ∈ R n 1 × n 2 × n 3 Z = U ∗ S ∗ V T \mathcal{Z}=\mathcal{U} * \mathcal{S} * \mathcal{V}^{\mathrm{T}} Z = U ∗ S ∗ V T U \mathcal{U} U V \mathcal{V} V n 1 × n 1 × n 3 n_1 \times n_1 \times n_3 n 1 × n 1 × n 3 n 2 × n 2 × n 3 n_2 \times n_2 \times n_3 n 2 × n 2 × n 3 S \mathcal{S} S n 1 × n 2 × n 3 n_1 \times n_2 \times n_3 n 1 × n 2 × n 3 ∗ * ∗
定义3 :给定Z ∈ R n 1 × n 2 × n 3 \mathcal{Z} \in \mathbb{R}^{n_1 \times n_2 \times n_3} Z ∈ R n 1 × n 2 × n 3 h = min ( n 1 , n 2 ) h=\operatorname{min}\left(n_1, n_2\right) h = min ( n 1 , n 2 ) Z \mathcal{Z} Z
公式 2 : ∥ Z ∥ s p = ( ∑ i = 1 n 3 ∥ Z ‾ ( i ) ∥ s p p ) 1 p = ( ∑ i = 1 n 3 ∑ j = 1 h σ j ( Z ‾ ( i ) ) p ) 1 p 公式2:\begin{aligned}
\|\mathcal{Z}\|_{sp} &=\left(\sum_{i=1}^{n_3}\left\|\overline{\mathcal{Z}}^{(i)}\right\|_{sp}^p\right)^{\frac{1}{p}} \\
&=\left(\sum_{i=1}^{n_3} \sum_{j=1}^h \sigma_j\left(\overline{\mathcal{Z}}^{(i)}\right)^p\right)^{\frac{1}{p}}
\end{aligned}
公式 2 : ∥ Z ∥ s p = ( i = 1 ∑ n 3 Z ( i ) s p p ) p 1 = ( i = 1 ∑ n 3 j = 1 ∑ h σ j ( Z ( i ) ) p ) p 1
其中p ∈ [ 0 , 1 ] p\in[0,1] p ∈ [ 0 , 1 ] σ j ( Z ‾ ( i ) ) \sigma_j(\overline{\mathcal{Z}}^{(i)}) σ j ( Z ( i ) ) Z ‾ ( i ) \overline{\mathcal{Z}}^{(i)} Z ( i ) p = 1 p=1 p = 1 Z ∈ R n 1 × n 2 × n 3 \mathcal{Z} \in \mathbb{R}^{n_1 \times n_2 \times n_3} Z ∈ R n 1 × n 2 × n 3 ∥ Z ∥ ∗ = ∑ i = 1 n 3 ∑ j = 1 h σ j ( Z ‾ ( i ) ) \|\mathcal{Z}\|_*=\sum_{i=1}^{n_3} \sum_{j=1}^h \sigma_j\left(\overline{\mathcal{Z}}^{(i)}\right) ∥ Z ∥ ∗ = ∑ i = 1 n 3 ∑ j = 1 h σ j ( Z ( i ) ) Z ∈ R n 1 × n 2 \mathbf{Z} \in \mathbb{R}^{n_1 \times n_2} Z ∈ R n 1 × n 2 Z \mathbf{Z} Z σ 1 , … , σ h \sigma_1, \ldots, \sigma_h σ 1 , … , σ h ∥ Z ∥ S p p = σ 1 p + ⋯ + σ h p , p > 0 \|\boldsymbol{Z}\|_{S_p}^p=\sigma_1^p+\cdots+\sigma_h^p, p>0 ∥ Z ∥ S p p = σ 1 p + ⋯ + σ h p , p > 0 lim p → 0 ∥ Z ∥ S p p = # { i : σ i ≠ 0 } = rank ( Z ) \lim _{p \rightarrow 0}\|\boldsymbol{Z}\|_{S_p}^p=\#\left\{i: \sigma_i \neq 0\right\}=\operatorname{rank}(\boldsymbol{Z}) lim p → 0 ∥ Z ∥ S p p = # { i : σ i = 0 } = rank ( Z ) p ∈ [ 0 , 1 ] p\in[0,1] p ∈ [ 0 , 1 ]
任务与存在的问题
现有的算法大都用于处理完整视图数据的聚类,然而在一些任务中存在不完整视图的情况,比如摄像机从不同角度拍摄时遇到的视角遮挡,光线变化,以及其他外部原因导致部分数据无法得到时,完整视图数据聚类的方法性能将会受到影响。
MFIMC的方法是应用矩阵分解和基于质心的公共正则化来寻找多视图数据的视图公共部分,然而这种方法没有考虑到数据的内部结构,这可能会导致compact的representation和distinguish-ability。
IMSC-AGL是不完整多视图聚类的代表方法,其引入一个常见的正则化项,使用低秩表征来从所有视图的低维表示中学习公共表示。但其仍然存在以下问题
其忽略了在聚类中扮演重要角色的不同视图之间的邻接矩阵的关系,因此多视图下的互补信息没有被充分利用。
学习到的图不能充分表示所有数据的聚类结构,因为其在学习图时没有考虑到在一个视图中缺失但是在其他视图中没有缺失的数据,学习到的图没有良好的聚类结构。
视图的亲和矩阵可以直接从视图中学习,而不丢失实例。然而,在实际应用中,由于每个视图不可避免地包含冗余和噪声,如照明变化,因此每个视图中只有部分内容有利于聚类。
主要工作和创新点
使用一个基于tensor Schatten p-norm的完整技术去学习一致性图。通过使用嵌入在不同视图的互补信息和高级信息,得到保留了未缺失数据之间关系的低秩图。
每个视图数据被分为view-important-content和view-unimportant-content,然后使用view-important-content的亲和矩阵取学习视图。
提出的方法
IMSC-AGL模型
给定一个多视图数据集{ X ( v ) } v = 1 V \left\{\mathbf{X}^{(v)}\right\}_{v=1}^V { X ( v ) } v = 1 V
公式 3 : min B ( v ) , E ( v ) , F ( v ) , U ∑ v ∥ B ( v ) ∥ ∗ + ∑ v λ 2 tr ( F ( v ) T L ‾ ( v ) F ( v ) ) + ∑ v λ 1 ∥ E ( v ) ∥ 1 + ∑ v λ 3 2 Γ ( F ( v ) , U ) s.t. Y ( v ) = Y ( v ) B ( v ) + E ( v ) , B ( v ) I = I 0 ≤ Z ( v ) ≤ 1 , B i , i ( v ) = 0 F ( v ) T F ( v ) = I , U T U = I 公式3:\begin{array}{c}
\min _{\mathbf{B}^{(v)}, \mathbf{E}^{(v)}, \mathbf{F}^{(v)}, \mathbf{U}} \sum_v\left\|\mathbf{B}^{(v)}\right\|_*+\sum_v \lambda_2 \operatorname{tr}\left(\mathbf{F}^{(v) T} \overline{\mathbf{L}}^{(v)} \mathbf{F}^{(v)}\right) \\
+\sum_v \lambda_1\left\|\mathbf{E}^{(v)}\right\|_1+\sum_v \frac{\lambda_3}{2} \Gamma\left(\mathbf{F}^{(v)}, \mathbf{U}\right) \\
\text { s.t. } \mathbf{Y}^{(v)}=\mathbf{Y}^{(v)} \mathbf{B}^{(v)}+\mathbf{E}^{(v)}, \quad \mathbf{B}^{(v)} \mathbf{I}=\mathbf{I} \\
0 \leq \mathbf{Z}^{(v)} \leq 1, \quad \mathbf{B}_{i, i}^{(v)}=0 \\
\mathbf{F}^{(v) T} \mathbf{F}^{(v)}=\mathrm{I}, \quad \mathbf{U}^T \mathbf{U}=\mathbf{I}
\end{array}
公式 3 : min B ( v ) , E ( v ) , F ( v ) , U ∑ v B ( v ) ∗ + ∑ v λ 2 tr ( F ( v ) T L ( v ) F ( v ) ) + ∑ v λ 1 E ( v ) 1 + ∑ v 2 λ 3 Γ ( F ( v ) , U ) s.t. Y ( v ) = Y ( v ) B ( v ) + E ( v ) , B ( v ) I = I 0 ≤ Z ( v ) ≤ 1 , B i , i ( v ) = 0 F ( v ) T F ( v ) = I , U T U = I
其中{ Y ( v ) } v = 1 V \left\{\mathbf{Y}^{(v)}\right\}_{v=1}^V { Y ( v ) } v = 1 V { X ( v ) } v = 1 V \left\{\mathbf{X}^{(v)}\right\}_{v=1}^V { X ( v ) } v = 1 V Y ( v ) ∈ R m v × n v \mathbf{Y}^{(v)} \in \mathbb{R}^{m_v \times n_v} Y ( v ) ∈ R m v × n v m v m_v m v n v n_v n v λ i ( i = 1 , 2 , 3 ) \lambda_i(i=1,2,3) λ i ( i = 1 , 2 , 3 ) E ( v ) \mathbf{E}^{(v)} E ( v ) Γ ( . ) \Gamma(.) Γ ( . ) U ∈ R n × c \mathbf{U} \in \mathbb{R}^{n \times c} U ∈ R n × c F ( v ) ∈ R n × c \mathbf{F}^{(v)} \in \mathbb{R}^{n \times c} F ( v ) ∈ R n × c c c c ∥ B ( v ) ∥ ∗ \left\|\mathbf{B}^{(v)}\right\|_* B ( v ) ∗ B ( v ) \mathbf{B}^{(v)} B ( v ) B ‾ ( v ) = H ( v ) T B ( v ) H ( v ) , B ‾ ( v ) ∈ R n × n \overline{\mathbf{B}}^{(v)}=\mathbf{H}^{(v) T} \mathbf{B}^{(v)} \mathbf{H}^{(v)}, \overline{\mathbf{B}}^{(v)} \in \mathbb{R}^{n \times n} B ( v ) = H ( v ) T B ( v ) H ( v ) , B ( v ) ∈ R n × n L ( t ) \mathbf{L}^{(t)} L ( t ) B ( v ) \mathbf{B}^{(v)} B ( v ) L ‾ ( v ) = H ( v ) T L ( v ) H ( v ) \overline{\mathbf{L}}^{(v)}=\mathbf{H}^{(v) T} \mathbf{L}^{(v)} \mathbf{H}^{(v)} L ( v ) = H ( v ) T L ( v ) H ( v ) H ( v ) ∈ R n b × n \mathbf{H}^{(v)} \in \mathbb{R}^{n_b \times n} H ( v ) ∈ R n b × n
公式 4 : H i , i ( v ) = { 1 , if y i ( v ) is the original instance x j ( v ) 0 , otherwise. 公式4:\mathbf{H}_{i, i}^{(v)}=\left\{\begin{array}{ll}
1, & \text { if } \mathbf{y}_{\mathrm{i}}^{(\mathrm{v})} \text { is the original instance } \mathbf{x}_{\mathrm{j}}^{(\mathrm{v})} \\
0, & \text { otherwise. }
\end{array}\right.
公式 4 : H i , i ( v ) = { 1 , 0 , if y i ( v ) is the original instance x j ( v ) otherwise.
问题公式化
本文提出的模型在IMSC-AGL模型的基础上,使用了相似度图中嵌入的低秩结构和相似性结构,并考虑了视图的特定属性,将其分为view-important-content和view-unimportant-content,并从view-important-content中学习亲和矩阵,最终的模型可以用下面的公式表示:
公式 5 : min Z ( v ) , E ( v ) , F ( v ) , D ( v ) , U ∑ v λ 1 ∥ E ( v ) ∥ 1 + ∑ v λ 4 ∥ D ( v ) ∥ F 2 + ∥ C ∥ s p p + ∑ v λ 3 ( c − tr ( F ( v ) F ( v ) T U U T ) ) + ∑ v λ 2 tr ( F ( v ) T H ( v ) T L ( v ) H ( v ) F ( v ) ) s.t. Y ( v ) = Y ( v ) ( Z ( v ) + D ( v ) ) + E ( v ) , Z ( v ) I = I , 0 ≤ Z ( v ) ≤ 1 , Z i , i ( v ) = 0 , F ( v ) T F ( v ) = I , U T U = I 公式5:\begin{array}{c}
\min _{\mathbf{Z}^{(v)}, \mathbf{E}^{(v)}, \mathbf{F}^{(v)}, \mathbf{D}^{(v)}, \mathbf{U}} \sum_v \lambda_1\left\|\mathbf{E}^{(v)}\right\|_1+\sum_v \lambda_4\left\|\mathbf{D}^{(v)}\right\|_F^2 \\
+\|\mathcal{C}\|_{sp}^p+\sum_v \lambda_3\left(c-\operatorname{tr}\left(\mathbf{F}^{(v)} \mathbf{F}^{(v) T} \mathbf{U} \mathbf{U}^T\right)\right) \\
+\sum_v \lambda_2 \operatorname{tr}\left(\mathbf{F}^{(v) T} \mathbf{H}^{(v) T} \mathbf{L}^{(v)} \mathbf{H}^{(v)} \mathbf{F}^{(v)}\right) \\
\text { s.t. } \mathbf{Y}^{(v)}=\mathbf{Y}^{(v)}\left(\mathbf{Z}^{(v)}+\mathbf{D}^{(v)}\right)+\mathbf{E}^{(v)}, \mathbf{Z}^{(v)} \mathrm{I}=\mathrm{I}, \\
0 \leq \mathbf{Z}^{(v)} \leq 1, \mathbf{Z}_{i, i}^{(v)}=0, \mathbf{F}^{(v) T} \mathbf{F}^{(v)}=\mathrm{I}, \mathbf{U}^T \mathbf{U}=\mathrm{I}
\end{array}
公式 5 : min Z ( v ) , E ( v ) , F ( v ) , D ( v ) , U ∑ v λ 1 E ( v ) 1 + ∑ v λ 4 D ( v ) F 2 + ∥ C ∥ s p p + ∑ v λ 3 ( c − tr ( F ( v ) F ( v ) T U U T ) ) + ∑ v λ 2 tr ( F ( v ) T H ( v ) T L ( v ) H ( v ) F ( v ) ) s.t. Y ( v ) = Y ( v ) ( Z ( v ) + D ( v ) ) + E ( v ) , Z ( v ) I = I , 0 ≤ Z ( v ) ≤ 1 , Z i , i ( v ) = 0 , F ( v ) T F ( v ) = I , U T U = I
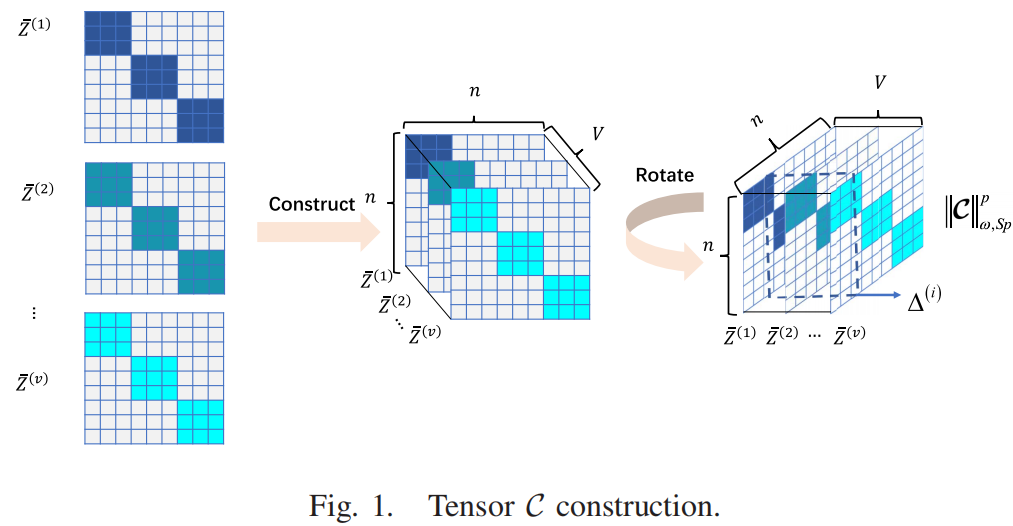
其中,上标v表示第v个视图,λ i ( i = 1 , 2 , 3 ) \lambda_i(i=1,2,3) λ i ( i = 1 , 2 , 3 ) E ( v ) \mathbf{E}^{(v)} E ( v ) D ( v ) D^{(v)} D ( v ) ∣ ∣ ⋅ ∣ ∣ n ||\cdot||_n ∣∣ ⋅ ∣ ∣ n ∣ ∣ ⋅ ∣ ∣ s p p ||\cdot||_{sp}^p ∣∣ ⋅ ∣ ∣ s p p F ( v ) ∈ R n × c \mathbf{F}^{(v)} \in \mathbb{R}^{n \times c} F ( v ) ∈ R n × c U ∈ R n × c \mathbf{U} \in \mathbb{R}^{n \times c} U ∈ R n × c I \mathbf{I} I t r ( ⋅ ) tr(\cdot) t r ( ⋅ ) c c c L ( v ) \mathbf{L}^{(v)} L ( v ) H ( v ) H^{(v)} H ( v ) Y ( v ) Z ( v ) \mathbf{Y}^{(v)}\mathbf{Z}^{(v)} Y ( v ) Z ( v ) Y ( v ) Z ( v ) \mathbf{Y}^{(v)}\mathbf{Z}^{(v)} Y ( v ) Z ( v ) C \mathcal{C} C Z ‾ v \overline{Z}^{v} Z v
最优化
(ps:由于过程比较硬核,我这里直接写结果)
为了让公式5可分解,这里引入了两个参数S \mathbf{\mathcal{S}} S W ( v ) \mathbf{W}^{(v)} W ( v )
公式 6 : L = ∥ S ∥ ⊛ p + ∑ v λ 1 ∥ E ( v ) ∥ 1 + λ 4 ∑ v ∥ D ( v ) ∥ F 2 + λ 2 ∑ v tr ( F ( v ) T H ( v ) T L ( v ) H ( v ) F ( v ) ) − ∑ v λ 3 tr ( F ( v ) F ( v ) T U U T ) + μ 2 ∥ C − S + Q μ ∥ F 2 + μ 2 ∑ v ∥ Y ( v ) − Y ( v ) ( Z ( v ) + D ( v ) ) − E ( v ) + C 1 ( v ) μ ∥ F 2 + μ 2 ∑ v ∥ Z ( v ) − W ( v ) + C 3 ( v ) μ ∥ F 2 − ∑ v ψ ( v ) T ( W ( v ) I − I ) , 公式6:\begin{aligned}
L=&\|\mathcal{S}\|_{\circledast}^p+\sum_v \lambda_1\left\|\mathbf{E}^{(v)}\right\|_1+\lambda_4 \sum_v\left\|\mathbf{D}^{(v)}\right\|_F^2 \\
&+\lambda_2 \sum_v \operatorname{tr}\left(\mathbf{F}^{(v) T} \mathbf{H}^{(v) T} \mathbf{L}^{(v)} \mathbf{H}^{(v)} \mathbf{F}^{(v)}\right) \\
&-\sum_v \lambda_3 \operatorname{tr}\left(\mathbf{F}^{(v)} \mathbf{F}^{(v) T} \mathbf{U} \mathbf{U}^T\right)+\frac{\mu}{2}\left\|\mathcal{C}-\mathcal{S}+\frac{\mathcal{Q}}{\mu}\right\|_F^2 \\
&+\frac{\mu}{2} \sum_v\left\|\mathbf{Y}^{(v)}-\mathbf{Y}^{(v)}\left(\mathbf{Z}^{(v)}+\mathbf{D}^{(v)}\right)-\mathbf{E}^{(v)}+\frac{\mathbf{C}_1^{(v)}}{\mu}\right\|_F^2 \\
&+\frac{\mu}{2} \sum_v\left\|\mathbf{Z}^{(v)}-\mathbf{W}^{(v)}+\frac{\mathbf{C}_3^{(v)}}{\mu}\right\|_F^2 \\
&-\sum_v \psi^{(v) T}\left(\mathbf{W}^{(v)} \mathbf{I}-\mathrm{I}\right),
\end{aligned}
公式 6 : L = ∥ S ∥ ⊛ p + v ∑ λ 1 E ( v ) 1 + λ 4 v ∑ D ( v ) F 2 + λ 2 v ∑ tr ( F ( v ) T H ( v ) T L ( v ) H ( v ) F ( v ) ) − v ∑ λ 3 tr ( F ( v ) F ( v ) T U U T ) + 2 μ C − S + μ Q F 2 + 2 μ v ∑ Y ( v ) − Y ( v ) ( Z ( v ) + D ( v ) ) − E ( v ) + μ C 1 ( v ) F 2 + 2 μ v ∑ Z ( v ) − W ( v ) + μ C 3 ( v ) F 2 − v ∑ ψ ( v ) T ( W ( v ) I − I ) ,
其中矩阵C 1 ( v ) , Q , C 3 ( v ) \mathbf{C}_1^{(v)}, \mathcal{Q}, \mathbf{C}_3^{(v)} C 1 ( v ) , Q , C 3 ( v ) ψ ( v ) \psi^{(v)} ψ ( v ) μ \mu μ
固定E ( v ) , F ( v ) , D ( v ) , U , S , W ( v ) \mathbf{E}^{(v)}, \mathbf{F}^{(v)}, \mathbf{D}^{(v)}, \mathbf{U}, \mathcal{S}, \mathbf{W}^{(v)} E ( v ) , F ( v ) , D ( v ) , U , S , W ( v ) Z ( v ) \mathbf{Z}^{(v)} Z ( v )
公式 7 : Z ( v ) = reshape [ Z ( v ) ( : ) ] n v × n v = reshape [ ( I ⊗ T 1 ( v ) + T 2 ( v ) T ⊗ I ) − 1 T 4 ( v ) ( : ) ] n v × n v 公式7:\begin{aligned}
\mathbf{Z}^{(v)} &=\operatorname{reshape}\left[\mathbf{Z}^{(v)}(:)\right]_{n_v \times n_v} \\
&=\operatorname{reshape}\left[\left(\mathbf{I} \otimes \mathbf{T}_1^{(v)}+\mathbf{T}_2^{(v)^T} \otimes \mathbf{I}\right)^{-1} \mathbf{T}_4^{(v)}(:)\right]_{n_v \times n_v}
\end{aligned}
公式 7 : Z ( v ) = reshape [ Z ( v ) ( : ) ] n v × n v = reshape [ ( I ⊗ T 1 ( v ) + T 2 ( v ) T ⊗ I ) − 1 T 4 ( v ) ( : ) ] n v × n v
其中,Z ( v ) ( : ) \mathbf{Z}^{(v)}(:) Z ( v ) ( : ) T 4 ( v ) ( : ) \mathbf{T}_4^{(v)}(:) T 4 ( v ) ( : ) Z ( v ) \mathbf{Z}^{(v)} Z ( v ) T 4 ( v ) = ( Y ( v ) Y ( v ) + I ) − 1 T 3 ( v ) ( H ( v ) H ( v ) T ) − 1 \mathbf{T}_4^{(v)}=(\mathbf{Y}^{(v)}\mathbf{Y}^{(v)}+I)^{-1}\mathbf{T}_3^{(v)}(\mathbf{H}^{(v)}\mathbf{H}^{(v)T})^{-1} T 4 ( v ) = ( Y ( v ) Y ( v ) + I ) − 1 T 3 ( v ) ( H ( v ) H ( v ) T ) − 1 T 1 v = ( Y ( v ) T Y ( v ) + I ) − 1 H ( v ) H ( v ) T \mathbf{T}_1^v=(\mathbf{Y}^{(v)T}Y^{(v)}+I)^{-1}\mathbf{H}^{(v)}\mathbf{H}^{(v)T} T 1 v = ( Y ( v ) T Y ( v ) + I ) − 1 H ( v ) H ( v ) T T 2 ( v ) = ( H ( v ) H ( v ) T ) − 1 \mathbf{T}_2^{(v)}=(\mathbf{H}^{(v)}\mathbf{H}^{(v)T})^{-1} T 2 ( v ) = ( H ( v ) H ( v ) T ) − 1 ⊗ \otimes ⊗ r e s h a p e [ Z ( v ) ( : ) ] n v × n v reshape[\left.\mathbf{Z}^{(v)}(:)\right]_{n_v \times n_v} res ha p e [ Z ( v ) ( : ) ] n v × n v Z ( v ) ( : ) \mathbf{Z}^{(v)}(:) Z ( v ) ( : ) Z ( v ) ∈ R n v × n v \mathbf{Z}^{(v)} \in \mathbb{R}^{n_v \times n_v} Z ( v ) ∈ R n v × n v
固定Z ( v ) , E ( v ) , F ( v ) , D ( v ) , U , W ( v ) \mathbf{Z}^{(v)}, \mathbf{E}^{(v)}, \mathbf{F}^{(v)}, \mathbf{D}^{(v)}, \mathbf{U}, \mathbf{W}^{(v)} Z ( v ) , E ( v ) , F ( v ) , D ( v ) , U , W ( v ) S \mathcal{S} S
公式 8 : S ∗ = Γ 1 μ ∗ ω [ C + Q μ ] = U ∗ ifft ( P 1 μ ∗ ω ( C + Q μ ‾ ) ∗ V T 公式8:\begin{aligned}
\mathcal{S}^* &=\Gamma_{\frac{1}{\mu}} * \omega\left[\mathcal{C}+\frac{\mathcal{Q}}{\mu}\right] \\
&=\mathcal{U} * \operatorname{ifft}\left(P_{\frac{1}{\mu}} * \omega\left(\overline{\mathcal{C}+\frac{\mathcal{Q}}{\mu}}\right) * \mathcal{V}^T\right.
\end{aligned}
公式 8 : S ∗ = Γ μ 1 ∗ ω [ C + μ Q ] = U ∗ ifft ( P μ 1 ∗ ω ( C + μ Q ) ∗ V T
其中P τ ⋅ n 3 ( A ‾ ) P_{\tau\cdot n_3}(\overline{\mathcal{A}}) P τ ⋅ n 3 ( A ) n 1 × n 2 × n 3 n_1 \times n_2 \times n_3 n 1 × n 2 × n 3
固定Z ( v ) , E ( v ) , F ( v ) , D ( v ) , U , S \mathbf{Z}^{(v)}, \mathbf{E}^{(v)}, \mathbf{F}^{(v)}, \mathbf{D}^{(v)}, \mathbf{U}, \mathcal{S} Z ( v ) , E ( v ) , F ( v ) , D ( v ) , U , S W ( v ) \mathbf{W}^{(v)} W ( v )
目标是
公式 9 : min w i , : ( v ) ( v ) ≥ 0 , w i , i ( v ) = 0 μ 2 ∥ W i , : ( v ) − ( R i , : ( v ) − λ 2 2 μ J i , : ( v ) ) ∥ 2 2 − ψ i ( b ) T ( W i , : ( v ) I − 1 ) 公式9:\begin{aligned}
\min _{\mathbf{w}_{i,:}^{(v)}{ }^{(v)} \geq 0, \mathbf{w}_{i, i}^{(v)}=0} \frac{\mu}{2} \| \mathbf{W}_{i,:}^{(v)}-\left(\mathbf{R}_{i,:}^{(v)}\right.&\left.-\frac{\lambda_2}{2 \mu} \mathbf{J}_{i,:}^{(v)}\right) \|_2^2 \\
-\psi_i^{(b) T}\left(\mathbf{W}_{i,:}^{(v)} \mathrm{I}-1\right)
\end{aligned}
公式 9 : w i , : ( v ) ( v ) ≥ 0 , w i , i ( v ) = 0 min 2 μ ∥ W i , : ( v ) − ( R i , : ( v ) − ψ i ( b ) T ( W i , : ( v ) I − 1 ) − 2 μ λ 2 J i , : ( v ) ) ∥ 2 2
其中P ( v ) = H ( v ) F ( v ) , R ( v ) = Z ( v ) + ( C 3 ( v ) / μ ) \mathbf{P}^{(v)}=\mathbf{H}^{(v)} \mathbf{F}^{(v)}, \mathbf{R}^{(v)}=\mathbf{Z}^{(v)}+\left(\mathbf{C}_3^{(v)} / \mu\right) P ( v ) = H ( v ) F ( v ) , R ( v ) = Z ( v ) + ( C 3 ( v ) / μ ) P i , : ( v ) \mathbf{P}_{i,:}^{(v)} P i , : ( v ) P j , : ( v ) \mathbf{P}_{j,:}^{(v)} P j , : ( v ) P ( v ) \mathbf{P}^{(v)} P ( v ) J i , j ( t ) = ∥ P i , : ( v ) − P j , : ( t ) ∥ 2 2 \mathbf{J}_{i, j}^{(t)}=\left\|\mathbf{P}_{i,:}^{(v)}-\mathbf{P}_{j,:}^{(t)}\right\|_2^2 J i , j ( t ) = P i , : ( v ) − P j , : ( t ) 2 2 ψ i ( v ) T \psi_i^{(v)T} ψ i ( v ) T ψ ( v ) \psi^{(v)} ψ ( v )
公式 10 : W i , i ( v ) = { 0 , j = i R i , j ( v ) − λ 2 2 μ J i , j ( v ) + ψ i ( v ) μ , otherwise. 公式10:\mathbf{W}_{i, i}^{(v)}=\left\{\begin{array}{ll}
0, & \mathrm{j}=\mathrm{i} \\
R_{i, j}^{(v)}-\frac{\lambda_2}{2 \mu} J_{i, j}^{(v)}+\frac{\psi_i^{(v)}}{\mu}, & \text { otherwise. }
\end{array}\right.
公式 10 : W i , i ( v ) = { 0 , R i , j ( v ) − 2 μ λ 2 J i , j ( v ) + μ ψ i ( v ) , j = i otherwise.
并且还需要经过W ( v ) = max ( W ( v ) , 0 ) \mathbf{W}^{(v)}=\max \left(\mathbf{W}^{(v)}, 0\right) W ( v ) = max ( W ( v ) , 0 ) W ( v ) W^{(v)} W ( v ) ψ i v \psi_i^v ψ i v
公式 11 : ψ i ( v ) = μ ( 1 − ∑ j = 1 , j ≠ i n v ( R i , j ( v ) − λ 2 2 μ J i , j ( v ) ) ) ( n v − 1 ) 公式11:\psi_i^{(v)}=\frac{\mu\left(1-\sum_{j=1, j \neq i}^{n_v}\left(\mathbf{R}_{i, j}^{(v)}-\frac{\lambda_2}{2 \mu} \mathbf{J}_{i, j}^{(v)}\right)\right)}{\left(n_v-1\right)}
公式 11 : ψ i ( v ) = ( n v − 1 ) μ ( 1 − ∑ j = 1 , j = i n v ( R i , j ( v ) − 2 μ λ 2 J i , j ( v ) ) )
固定Z ( v ) , F ( v ) , D ( v ) , U , S , W ( v ) \mathbf{Z}^{(v)}, \mathbf{F}^{(v)}, \mathbf{D}^{(v)}, \mathbf{U}, \mathcal{S}, \mathbf{W}^{(v)} Z ( v ) , F ( v ) , D ( v ) , U , S , W ( v ) E ( v ) \mathbf{E}^{(v)} E ( v )
公式 12 : E ( v ) = ϑ λ 1 / μ ( Y ( v ) − Y ( v ) ( Z ( v ) + D ( v ) ) + C 1 ( v ) μ ) , 公式12:\mathbf{E}^{(v)}=\vartheta_{\lambda_1 / \mu}\left(\mathbf{Y}^{(v)}-\mathbf{Y}^{(v)}\left(\mathbf{Z}^{(v)}+\mathbf{D}^{(v)}\right)+\frac{\mathbf{C}_1^{(v)}}{\mu}\right),
公式 12 : E ( v ) = ϑ λ 1 / μ ( Y ( v ) − Y ( v ) ( Z ( v ) + D ( v ) ) + μ C 1 ( v ) ) ,
其中ϑ \vartheta ϑ ϑ v ( Z ) = Z ‾ \vartheta_v(\mathcal{Z})=\overline{\mathcal{Z}} ϑ v ( Z ) = Z
公式 13 : z ˉ n 1 n 2 n 3 = { sgn ( z n 1 n 2 n 3 ) ( ∣ z n 1 n 2 n 3 ∣ − v ) , ∣ z n 1 n 2 n 3 ∣ > v , 0 , ∣ z n 1 n 2 n 3 ∣ ≤ v 公式13:\bar{z}_{n_1 n_2 n_3}=\left\{\begin{array}{ll}
\operatorname{sgn}\left(z_{n_1 n_2 n_3}\right)\left(\left|z_{n_1 n_2 n_3}\right|-v\right), & \left|z_{n_1 n_2 n_3}\right|>v, \\
0, & \left|z_{n_1 n_2 n_3}\right| \leq v
\end{array}\right.
公式 13 : z ˉ n 1 n 2 n 3 = { sgn ( z n 1 n 2 n 3 ) ( ∣ z n 1 n 2 n 3 ∣ − v ) , 0 , ∣ z n 1 n 2 n 3 ∣ > v , ∣ z n 1 n 2 n 3 ∣ ≤ v
固定Z ( v ) , F ( v ) , E ( v ) , U , S , W ( v ) \mathbf{Z}^{(v)}, \mathbf{F}^{(v)}, \mathbf{E}^{(v)}, \mathbf{U}, \mathcal{S}, \mathbf{W}^{(v)} Z ( v ) , F ( v ) , E ( v ) , U , S , W ( v ) D ( v ) \mathbf{D}^{(v)} D ( v )
公式 14 : D ( v ) = ( I + Y ( v ) T Y ( v ) ) − 1 Y ( v ) T M 4 ( v ) 公式14:\mathbf{D}^{(v)}=\left(\mathrm{I}+\mathbf{Y}^{(v) T} \mathbf{Y}^{(v)}\right)^{-1} \mathbf{Y}^{(v) T} \mathbf{M}_4^{(v)}
公式 14 : D ( v ) = ( I + Y ( v ) T Y ( v ) ) − 1 Y ( v ) T M 4 ( v )
其中M 4 ( v ) = Y ( v ) − Y ( v ) Z ( v ) − E ( v ) + C 1 ( v ) μ \quad \mathbf{M}_4^{(v)}=\mathbf{Y}^{(v)}-\mathbf{Y}^{(v)} \mathbf{Z}^{(v)}-\mathbf{E}^{(v)}+\frac{\mathbf{C}_1^{(v)}}{\mu} M 4 ( v ) = Y ( v ) − Y ( v ) Z ( v ) − E ( v ) + μ C 1 ( v )
固定Z ( v ) , E ( v ) , D ( v ) , U , S , W ( v ) \mathbf{Z}^{(v)}, \mathbf{E}^{(v)}, \mathbf{D}^{(v)}, \mathbf{U}, \mathcal{S}, \mathbf{W}^{(v)} Z ( v ) , E ( v ) , D ( v ) , U , S , W ( v ) F ( v ) \mathbf{F}^{(v)} F ( v )
通过考虑下面的最小化问题得到每一个视图的聚类指标矩阵F ( v ) \mathbf{F}^{(v)} F ( v )
公式 15 : min F ( v ) T F ( v ) = I λ 2 tr ( F ( v ) T H ( v ) T L ( v ) H ( v ) F ( v ) ) − λ 3 tr ( F ( v ) F ( v ) T U U T ) ⇔ max F ( v ) T F ( v ) = I tr ( F ( v ) T ( λ 3 U U T − λ 2 H ( v ) T L ( v ) H ( v ) ) F ( v ) ) 公式15:\begin{array}{l}
\min _{\mathbf{F}^{(v) T} \mathbf{F}^{(v)}=\mathrm{I}} \lambda_2 \operatorname{tr}\left(\mathbf{F}^{(v) T} \mathbf{H}^{(v) T} \mathbf{L}^{(v)} \mathbf{H}^{(v)} \mathbf{F}^{(v)}\right)\\
-\lambda_3 \operatorname{tr}\left(\mathbf{F}^{(v)} \mathbf{F}^{(v) T} \mathbf{U} \mathbf{U}^T\right)\\
\Leftrightarrow\\
\max _{\mathbf{F}^{(v) T} \mathbf{F}^{(v)}=\mathrm{I}} \operatorname{tr}\left(\mathbf{F}^{(v) T}\left(\lambda_3 \mathbf{U} \mathbf{U}^T-\lambda_2 \mathbf{H}^{(v) T} \mathbf{L}^{(v)} \mathbf{H}^{(v)}\right) \mathbf{F}^{(v)}\right)
\end{array}
公式 15 : min F ( v ) T F ( v ) = I λ 2 tr ( F ( v ) T H ( v ) T L ( v ) H ( v ) F ( v ) ) − λ 3 tr ( F ( v ) F ( v ) T U U T ) ⇔ max F ( v ) T F ( v ) = I tr ( F ( v ) T ( λ 3 U U T − λ 2 H ( v ) T L ( v ) H ( v ) ) F ( v ) )
通过使用特征值分解,F ( t ) \mathbf{F}^{(t)} F ( t ) λ 3 U U T − λ 2 H ( v ) T L ( v ) H ( v ) \lambda_3 \mathbf{U} \mathbf{U}^T-\lambda_2 \mathbf{H}^{(v) T} \mathbf{L}^{(v)} \mathbf{H}^{(v)} λ 3 U U T − λ 2 H ( v ) T L ( v ) H ( v )
固定Z ( v ) , F ( v ) , D ( v ) , E ( v ) , S , W ( v ) \mathbf{Z}^{(v)}, \mathbf{F}^{(v)}, \mathbf{D}^{(v)}, \mathbf{E}^{(v)}, S, \mathbf{W}^{(v)} Z ( v ) , F ( v ) , D ( v ) , E ( v ) , S , W ( v ) U \mathbf{U} U
可以得到公共聚类表示U \mathbf{U} U
公式 16 : min U T U = 1 − ∑ b λ 3 tr ( F ( v ) F ( v ) T U U T ) ⇔ max U T U = I tr ( U T ( ∑ t F ( v ) F ( v ) T ) U ) 公式16:\begin{array}{l}
\min _{\mathbf{U}^T \mathbf{U}=1}-\sum_b \lambda_3 \operatorname{tr}\left(\mathbf{F}^{(v)} \mathbf{F}^{(v) T} \mathbf{U} \mathbf{U}^T\right) \\
\quad \Leftrightarrow \\
\max _{\mathbf{U}^T \mathbf{U}=I} \operatorname{tr}\left(\mathbf{U}^T\left(\sum_t \mathbf{F}^{(v)} \mathbf{F}^{(v) T}\right) \mathbf{U}\right)
\end{array}
公式 16 : min U T U = 1 − ∑ b λ 3 tr ( F ( v ) F ( v ) T U U T ) ⇔ max U T U = I tr ( U T ( ∑ t F ( v ) F ( v ) T ) U )
使用矩阵∑ v F ( v ) F ( v ) T \sum_v \mathbf{F}^{(v)} \mathbf{F}^{(v) T} ∑ v F ( v ) F ( v ) T U \mathbf{U} U
固定其他变量,更新C 1 ( v ) , Q , C 3 ( v ) \mathbf{C}_1^{(v)},\mathcal{Q},\mathbf{C}_3^{(v)} C 1 ( v ) , Q , C 3 ( v ) μ \mu μ
公式 17 : C 1 ( v ) = C 1 ( v ) + μ ( Y ( v ) − Y ( v ) ( Z ( v ) + D ( v ) ) − E ( v ) ) C 3 ( v ) = C 3 ( v ) + μ ( Z ( v ) − W ( v ) ) Q = Q + μ ( C − S ) μ = min ( ρ μ , μ 0 ) 公式17:\begin{aligned}
\mathbf{C}_1^{(v)} &=\mathbf{C}_1^{(v)}+\mu\left(\mathbf{Y}^{(v)}-\mathbf{Y}^{(v)}\left(\mathbf{Z}^{(v)}+\mathbf{D}^{(v)}\right)-\mathbf{E}^{(v)}\right) \\
\mathbf{C}_3^{(v)} &=\mathbf{C}_3^{(v)}+\mu\left(\mathbf{Z}^{(v)}-\mathbf{W}^{(v)}\right) \\
\mathcal{Q} &=\mathcal{Q}+\mu(\mathcal{C}-\mathcal{S}) \\
\mu &=\min \left(\rho \mu, \mu_0\right)
\end{aligned}
公式 17 : C 1 ( v ) C 3 ( v ) Q μ = C 1 ( v ) + μ ( Y ( v ) − Y ( v ) ( Z ( v ) + D ( v ) ) − E ( v ) ) = C 3 ( v ) + μ ( Z ( v ) − W ( v ) ) = Q + μ ( C − S ) = min ( ρ μ , μ 0 )
其中ρ \rho ρ μ 0 \mu_0 μ 0
为了得到最终的聚类结果,本文在公共矩阵U \mathbf{U} U
不完全多视图聚类的视图一致性学习算法
输入:不完整多视图数据Y ( v ) \mathbf{Y}^{(v)} Y ( v ) H ( v ) \mathbf{H}^{(v)} H ( v ) λ 1 , λ 2 , λ 3 , λ 4 \lambda_1,\lambda_2,\lambda_3,\lambda_4 λ 1 , λ 2 , λ 3 , λ 4
初始化:和IMSC-AGL一样初始化Z ( v ) , F ( v ) \mathbf{Z}^{(v)},\mathbf{F}^{(v)} Z ( v ) , F ( v ) U \mathbf{U} U μ 0 = 10 8 \mu_0=10^8 μ 0 = 1 0 8 ρ = 1.1 \rho=1.1 ρ = 1.1 μ = 10 − 2 \mu=10^{-2} μ = 1 0 − 2
begin:
while 没收敛 do:
for v from 1 to V do:
通过公式7计算Z ( v ) \mathbf{Z}^{(v)} Z ( v )
通过公式8计算S \mathcal{S} S
通过公式10和11计算W ( v ) \mathbf{W}^{(v)} W ( v ) ψ ( v ) \psi^{(v)} ψ ( v ) W ( v ) = max ( W ( v ) , 0 ) \mathbf{W}^{(v)}=\max \left(\mathbf{W}^{(v)}, 0\right) W ( v ) = max ( W ( v ) , 0 )
通过公式12计算E ( v ) \mathbf{E}^{(v)} E ( v )
通过公式14计算D ( v ) \mathbf{D}^{(v)} D ( v )
使用公式15计算F ( v ) \mathbf{F}^{(v)} F ( v )
使用公式17分别计算C 1 ( v ) , Q , C 3 ( v ) \mathbf{C}_1^{(v)},\mathcal{Q},\mathbf{C}_3^{(v)} C 1 ( v ) , Q , C 3 ( v )
使用公式16计算聚类矩阵U \mathbf{U} U
使用公式17计算乘法参数μ \mu μ
输出:U \mathbf{U} U