「论文阅读」NetRL: Task-aware Network Denoising via Deep Reinforcement Learning
论文:NetRL: Task-aware Network Denoising via Deep Reinforcement Learning
作者:Jiarong Xu; Yang Yang; Shiliang Pu; Yao Fu; Jun Feng; Weihao Jiang; Jiangang Lu; Chunping Wang
时间:2022-7
原文摘要
Network data is mostly hard to obtain and error-prone. However, most existing works assume that the studied network represents a perfect and complete picture of topological structure; nevertheless, it is rarely the case in real-world situations. Such studies, performing downstream applications (e.g., vertex classification, link prediction, etc.) directly on original networks, will suffer greatly due to the noise and deteriorate the application performance. In this paper, we propose NetRL, a novel method for network denoising, that works by creating missing edges and removing incorrect edges from a noisy network, thereby improving its quality and representative power. In particular, NetRL turns the problem of network denoising into edge sequences generation, which can be formulated as a Markov Decision Process. By doing this, NetRL takes the complex long-term dependency between edge creations into consideration, i.e., the existence of an edge depends on which edges have been generated so far. It further takes advantage of downstream task to guide the network denoising process, by providing a deep reinforcement learning framework to conduct direct optimization on this task-specific objective. As a result, NetRL ensures that the denoised network not only satisfies the topological property of the original network, but also improves the performance of the downstream application. Experimental results on real-world networks show that, comparing with several baseline methods, NetRL can denoise networks effectively with better performance for vertex classification. Meanwhile, NetRL can better preserve original network’s properties (e.g., degree distribution and clustering coefficient. Our implementation is available at: https://github.com/galina0217/NetRL.
任务与存在的问题
任务:使用一种方式,减少对目标有影响的噪声边,同时增加对目标有帮助的边,生成新的clean图,用于下游任务。
- 现有的大多数工作都假设研究网络是一个完美且完整的拓扑结构,然而这在现实情况中很少。
- 直接在原始图上进行下游任务通常会受到原始图中的噪声的影响,从而使得应用的性能下降。
- 直接使用链路预测的方式去判断图节点的边忽略了边的创建之间的复杂的、非局部的、长期的依赖关系
- 降低性能的边缘通常含有噪声,通常会使用下游任务的表现作为RL的奖励,但是这会使得奖励延迟
- 由于缺乏针对有噪声边缘的监督信息,这限制了传统机器学习技术的可行性。
主要的工作和创新点
提出了一个新颖的降噪网络模型NetRL(Network Denoising via Reinforcement Learning)
- 使用RL agent对迄今为止已经生成的边采取最好的action,因此能够处理长期的,非局部的依赖关系
- NetRL是任务驱动的,其自然地利用了下游任务提供的信息
- 去噪过程可以通过试错搜索来学习,试图产生对更优化的路径的强烈偏好,并在给定的噪声网络和下游任务中获得奖励或惩罚的反馈,因此不需要关于哪些边是有噪声的监督信息
- 提出一种多样化的经验回放机制(Diversified Experience Replay mechanism),以确保RL代理能够有效地从更多样化的transitions中学习,并充分利用延迟的奖励。
提出的方法
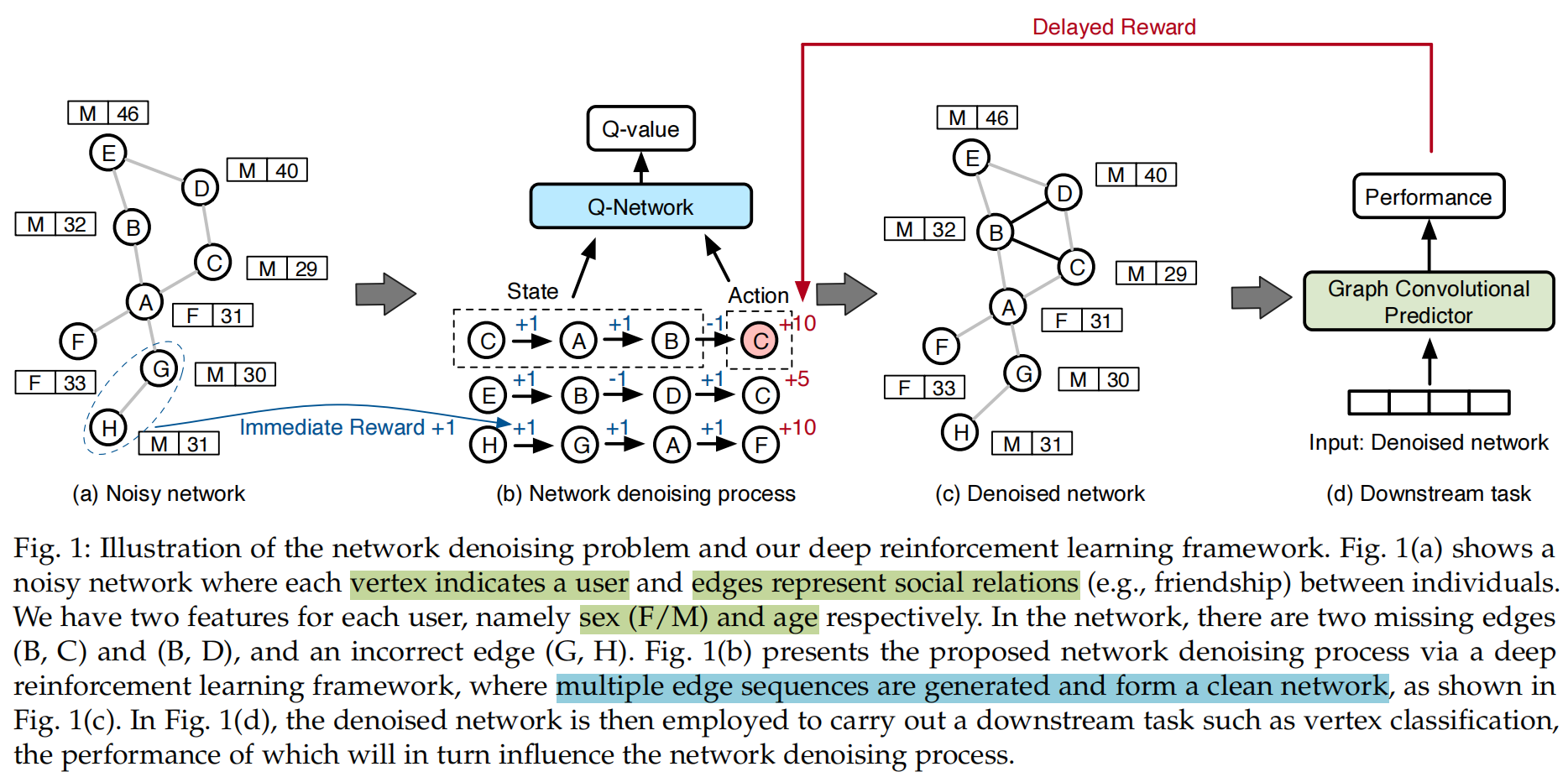
一般说明
给定一个噪声网络,本文要生成新边集合形成一个干净的网络。其中引入了一个RL agent去去除噪声边。具体来说,agent从一个随机的节点中开始,然后构建一个序列,下一步,agent做出action,选择一个要连接到节点的节点,然后在两个节点之间构建一条边并将节点加入到序列中,得到。这个序列被称为生成的边序列(简称边序列),定义序列的集合为。
State:当前节点的特征和拓扑信息以及当前序列 中每个顶点的拓扑信息组成,特征就是数据集中的节点特征,如果没有就不用了,拓扑信息是使用网络嵌入技术得到的representation。
Action:要加入当前边缘序列的节点作为action
Reward:分成两部分:原始网络的奖励,下游应用的奖励。这两种奖励共同确保了我们的去噪网络将保留,甚至更好地代表原始网络的拓扑信息,并进一步有利于下游应用程序。
Q-Network结构
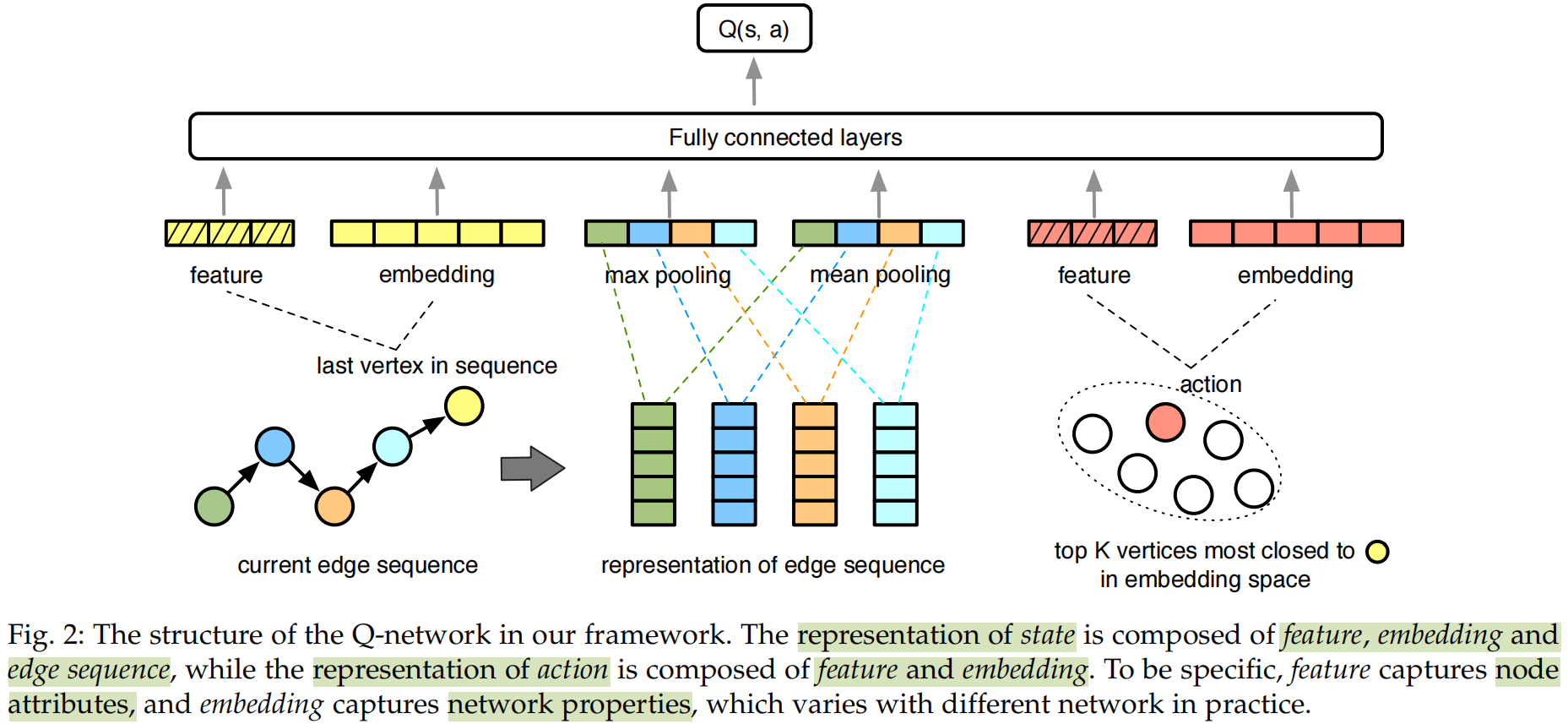
在本文中使用Q-network去近似action-value函数。由于图中的节点很多,因此状态空间和动作空间非常大。为了解决这一问题,本文将状态和动作到编码到一个连续的低维空间中。
state 是一个连续的实值向量,其编码以下信息:
- 节点的拓扑representation和特征
- 从生成边序列中得到的序列信息
本文使用向量去定义边序列,其中表示序列中第i个顶点的索引
其中,时间窗的长度为表示RL Agent可以观察到的最大视图范围,是通过网络嵌入算法得到的节点的拓扑representation。本文在当前边序列的representation上执行最大池化和平均池化,去减小空间维度,简化模型复杂度。
使用向量对state 进行编码,其拼接了的特征向量和拓扑representation 以及边缘序列中其他节点的表征,其表示如下:
在的时候,agent只使用一个随机的节点开始生成边缘序列。
对于action ,假设选中的节点为,那么动作可以用他的特征和拓扑representation 进行编码:
为了减少计算复杂性并提高模型的有效性,只有和的拓扑representation足够接近时,才考虑在之后添加。
Q-network将当前顶点的representation,之前遍历的顶点以及要到达的下一个顶点作为图二所示的神经网络输入,他输出以及近似于的神经元:
其中表示向量拼接,表示带有参数的全连接神经网络。
奖励计算
奖励用到了即时奖励和延迟奖励。在训练过程中,定义终止state为:当agent经过一个给定长度的决策序列时触发。就是在终止state触发时得到,在其他时候得到。
即时奖励:
- 去噪网络应该保护原始图的拓扑信息
- 相似的节点更可能彼此相连
因此,本文定义即时奖励由两个部分组成:
- ,由保护原始图的拓扑信息这个动机得到
- ,由相似的节点更可能彼此相连这个动机得到
其中是超参数,用于调节和之间的权重。
用于捕获原始网络的主要拓扑结构,假设最后一个加入当前边序列的节点为,下一个要被添加的节点,当要创建的边存在与原图中时,会给出一个正向的奖励。同时如果已经在当前序列中被添加过了,就不会再给出正向的奖励了,这个过程可以用下面的公式表示:
使用顶点标签来表示:
其中表示的标签,表示如果在训练数据中缺少该标签。本文假设所有的数据集中都缺失了的标签。
延迟奖励:
延迟奖励表示的是去噪网络对下游任务的贡献,它是由分类器或特定任务的机器学习模型估计的。在本文中,使用GCN作为分类器,可以将这个奖励定义为:
其中是去噪网络的邻接矩阵,是原始图的邻接矩阵,是特征矩阵,是训练标签,是深度分类器的第b个隐藏层。是预测模型,其输出就是预测的标签,是评价指标(这里使用的是f1 score),表示这个预测的标签和ground truth的接近程度。是约束项,可以被认为是延迟奖励和即时奖励的权衡参数。
模型学习
学习过程
本文使用GCN计算出延迟奖励,并使得总的奖励最大,因此对于GCN部分的损失函数可以用交叉熵损失函数表示:
其中是训练集的坐标,和是分别是节点的真实标签和预测标签。
一旦得到高质量的延迟奖励,agent也能从中学到更多的东西,同时,一旦只能体根据做出高价值的动作,也能提高GCN的表现。本文使用Double DQN去训练RL框架。本文希望Q-Network能够很好地拟合总奖励,以估计每个决策的效用,于是可以吧这个损失函数定义为:
其中是折扣因子,使用Adam去优化这个目标,为了得到稳定更新,本文使用target Q-network的advantage,其被参数化为,orginal Q-network的参数为,target Q-network的参数更新速度比original Q-network慢得多,只能定期替换
多样化经验回放
DQN能够使用回放存储中的经验,更新Q-network的参数,但是需要解决两个问题
- 当训练过程相对稳定时,总会有一些特定的state-action对具有较大的Q-Value,这产生了许多重复和冗余的经验。这也使得回放的经验中缺乏多样性,训练效率下降。
- 延迟奖励比即时奖励少很多。因此本文将回放内存分为和两部分,同时这两个内存有不同的容量。但这两个容量之间的比例仍然难以确定。
于是本文提出了新的多样化经验回放机制,为了解决第一个问题,本文首先提出了不重复的transitions,然后在他们中执行uniform sampling。如果未重复使用的样本数量不满足所需的样本量,剩余的部分将会从回放内存中采样。为了解决第二个问题,本文定义了一个在time t时,和之间的可变容量比
其中约束了的最小值,是的初值,被设定为一个相对较大的值,因为即时奖励在训练的早期阶段更重要。是衰减率。是当前的步数。是衰减的步数。
NetRL算法可以用下面的算法表示:
The NetRL algorithm
输入:迭代次数episodes,边序列的最大长度,target network更新周期,greedy系数,学习率,是Q-network的参数
- 初始化当前的步数:step=0
- 初始化目标网络:=
- repeat
- 随机选择的节点
- 初始化状态
- for t=0 to |L| do
- 通过概率选择一个随机动作
- 否则选择
- 在模拟器中执行动作,根据公式5观察即时奖励和下一个状态
- 设置
- 存储 到中
- if t==|L| then
- 使用重构去噪网络
- 根据公式8使用GCN计算延迟奖励
- 设置
- 存储 到中
- end if
- 根据公式12,使用容量比,从和中采样的minibatch
- 更新
- if then
- 设置
- end if
- end for
- until 迭代结束









