「论文笔记」HET-GMP: A Graph-based System Approach to Scaling Large Embedding Model Training
简要
Problem:
更新和检索共享的大规模embedding参数通常主导分布式训练周期,这是一个主要的embedding模型训练的阻碍,这将到严重的可拓展性(scalability)的问题
现有的分布式机器学习系统使用参数服务器(PS)或基于AllReduce的方法来拓展模型。其中,通过有限的带宽链路对共享嵌入参数的系数读取和更新是这种方法最低效的部分。
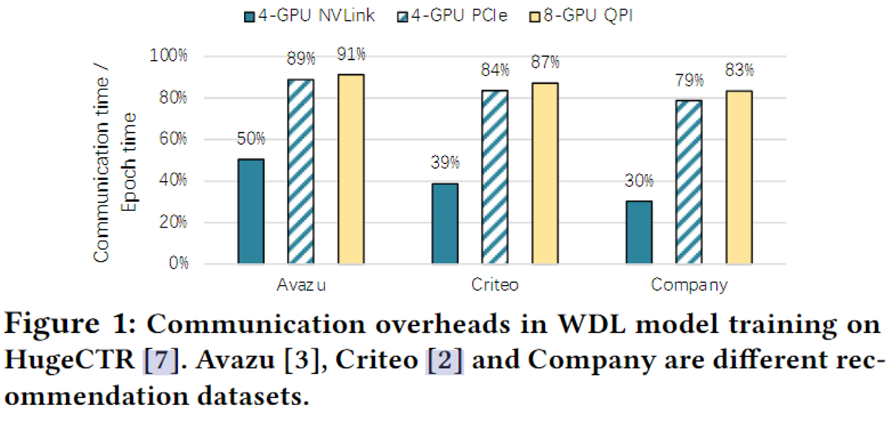
从图中可以看出,90%的训练时间花费在获取和更新嵌入参数上,这在训练中期中占主导地位。
HET-GMP的数据建模方式:
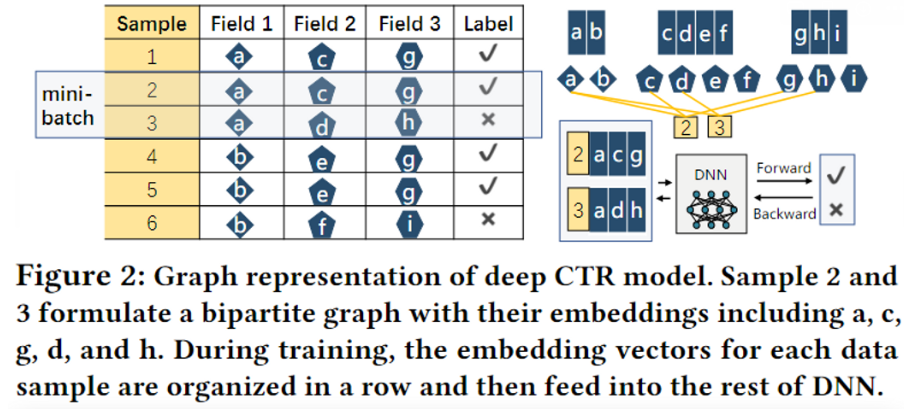
假设有左边的一个嵌入表,然后每一行表示一个数据,一行中的每一个元素表示样本在每一个field的embedding 向量。其构造二分图的模式,两边的节点分别表示embedding向量和数据样本每一个embedding指向对应的样本。
从图中可以看出ab,cdef,ghi分别存储在不同分区中(或者说不同的节点上),embedding的使用可能存在一定的局部性和偏度。这就给出了两个优化思路
- 通过有意识的位置布局优化,大多数的embedding可以放置在少数worker上,并在本地执行以减少通信。
- 在每个worker上复制hot embedding,可以有效减少网络带宽。
HET-GMP使用的两种机制:
- 复合图分区(Hybird graph partition)
- 目的:找到更加具有局部性和负载均衡的分区
- 1D edge-cut:均匀地将数据样本(23)和embedding顶点(abcdefghi)分配给worker,最小化跨worker的边数
- 2D vetex-cut:通过切割和复制节点在worker之间均匀分配high-degree节点的边缘
- 基于图的一致性模型(Graph-base Consistency model)
- 在2D vetex-cut中涉及到了复制节点,因此在更新的时候就要考虑到节点的一致性了
- 在HET-GMP中面临一个从来没被解决的技术难点:底层图结构揭示了跨embedding的更新依赖关系
- 通过引入两个同步点提出了一个新颖的有界同步
- 读取特定embedding顶点时,跨副本的intra-embedding同步
- 执行计算时,特定数据样本顶点所使用的inter-embedding同步
Contribution:
- 提出新颖的基于图的方法,促进训练大型embedding模型的可拓展性
- 提供有效的复合图分区算法,实现在分布式训练的平衡和区域感知
- 引入基于图的有界同步,并证明其收敛性
观察和机遇
- 局部性
- 训练数据和参数具有很好的共现关系(co-occurrence)
- 将共现的embedding和相应的数据样本放入到同一个worker中,可以改善access的局部性
- 偏度
- embedding nodes具有高度便宜的幂率分布(power-low degree distributions,即访问频率)
- 在本地进行大程度(高频)的缓存embedding,以进一步见底远程access的成本。
HET-GMP的设计
HET-GMP——新颖的大规模嵌入模型训练系统
图表示:
二分图
x表示的是embedding节点
表示的是样本节点
边表示当前样本节点有对应的类别特征(embedding)
embedding梯度
复合图分区
解决问题:将图划分到适当的worker上,从而减小embedding或gradient的通信开销,实现负载均衡
-
步骤1:边切分区
- 给定分区,节点v将被分配到分区
- 使其满足:
- 其中的定义为
- 其中表示在第i个GPU上的GPU内通信开销
- 表示平衡公式
与分区上的节点的边切相同
函数count(x,i)表示embedding x被在第i个分区中的数据样本使用的次数
为了反映网络带宽不均衡的问题,本文分析了GPU-GPU之间的通信速度,并将其制定为权重矩阵,当计算出edge-cut时,将结果与对应的权重进行相乘。实现在整个数据图分区中跨分区的边的数量能够适应不同worker之间不均衡的带宽。
平衡公式可以解释为添加结点v到分区的边界开销,其用于平衡不同分区之间的工作流。
其中 , 和 是超参数
和 是平衡公式,分别用于平衡每个分区的样本和embedding节点。他们描述的是样本和embedding结点在分区(比如 和 )和对于所有分区的平均数量(比如, and )之间的差异。第三项用于平衡所有分区中GPU之间的通信
其描述的是在第i个GPU不均衡的通信和对于所有GPU的平均通讯之间的差异。
-
步骤2:点切分区
点切会复制具有较多度数的结点,以此减小通信开销。通过将单个节点的边分割到多个worker上的方式进一步实现2D分区(点切)。这是在远程访问通信开销和冗余复制开销的一个权衡。
定义这个方法的分数公式如下,首先给定1D分区,当 并且 时,embedding节点 会有比其他的embedding节点更高的优先级复制到分区上。其中
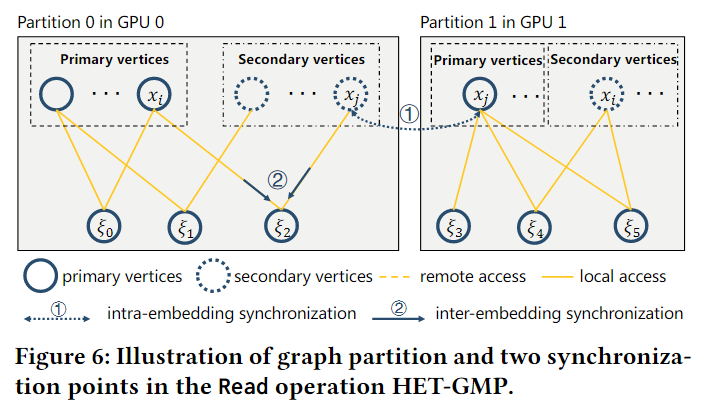
如上图所示,对于每个worker的局部embedding有两种类型的结点,1D分区不重合的部分将作为每个worker的主结点,复制到其他分区的embedding节点就叫做第二结点。按照上面的例子,xi是GPU0的主节点,是GPU1的第二节点,xj是GPU1的主节点,是GPU0的第二结点。 对于每个embedding只有一个主结点,而在不同的worker上会有多个第二结点。平衡的图分区能够最小化远程访问开销,并且复制能够进一步促进局部化。
基于图的边界同步
目的:解决点切引入的跨分区建模的一致性问题
嵌入模型的分布式训练有两个同步点
- 读取特定embedding时的副本
- 统一数据结点使用多个embedding时的副本
如图6所示,embedding的主结点总是保持最新的,因此可以直接在本地访问,对于第二结点,会执行两个同步以保证边缘过时性:
-
embedding内的异步
和图6中的1相同,当一个数据样本读取embedding X的集合时,对于每个embedding,首先会检查局部第二embedding结点的版本是否从主结点中更新了s次。如果不是,则执行局部第二embedding以及其远程的主节点的异步。
-
embedding间的异步
在收集完全嵌入 X的集合后,会检查embedding対 的边界版本是否为s。(即embedding的某个结点是否比其他的相关节点的版本落后太多)。如果落后太多的话,就会向embedding远端的主结点进行异步,或者使worker进入等待状态直至副本不再过于陈旧。
这可以保证嵌入结点的质量不受其他相关嵌入结点过于陈旧的影响。
为了实现这两个异步,本文为在worker k上的embedding结点保留了一个时钟,用于记录在这个副本上的累积更新次数。一旦embedding没能通过陈旧性检查(时钟差异超过阈值s),则会与副本的主结点进行异步。
同时为了减轻不同embedding访问频率的影响,使用时钟对在worker 上的embedding对进行检查时,假设两个嵌入的访问频率分别是并且,那么两个embedding之间的归一化时钟差异为。








