「论文笔记」AutoShard: Automated Embedding Table Sharding for Recommender Systems

简要

problem：大规模的embedding表参数会影响到推荐系统embedding模型的训练过程，这些大规模的embedding表如果使用不平衡的分布式存储方式，会严重影响模型的执行效率。这就涉及到一个挑战：embedding表分片问题（embedding table sharding）

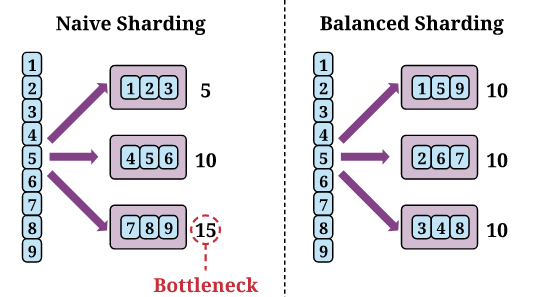
如上图所示，蓝色的框表示一个embedding表，然后框内的数字表示执行操作执行时间的成本。紫色的框表示一个分片（sharding）旁边的数字表示这个分片的执行时间成本。

如果在分片过程中没有考虑到分片的平衡（图左边），就可能会导致GPU之间的不平衡，其中所有的GPU必须强制等待最慢的GPU（图中的bottleneck）。相反，如果分片是平衡的（图右边），就可以通过减小等待时间来显著加速embedding的操作。

因为sharding内部是并行执行的，所以sharding内部的执行时间是显著小于所有embedding表的执行时间之和的，比如 $5<1+2+3$ ， $10<4+5+6$

在这个问题中有两个重要的目标：

需要有效地对开销进行评估，以此作为优化目标
需要一个有效的算法去解决NP难的分区问题

contribution: 提出了基于开销模型和强化学习的解决方案——AutoShard。其将表分片作为一个马尔可夫决策问题(MDP)，在每一步中分配一个表到一个分片中，在所有表分配完成后，将得到一个表示分片质量的奖励。

通过FBGEMM的一个现代化的embedding bag实现的案例研究，深入分析embedding操作开销的主要因素
提出AutoShard，利用RL解决分片问题
进行了大量实验，表明训练好的AutoShard可以应用在广泛的分片任务中。

分片问题的定义

$\mathcal{T}_p=\left\{T_1, T_2, \ldots, T_N\right\}$ ：表示embedding表池，其中我那个N是池中表的数量

分片任务表示为 $S=(\mathcal{T}, \mathcal{D}, \mathcal{M})$ ，其中 $\mathcal{T} \subseteq \mathcal{T}_p$ 是表的子集， $\mathcal{D}=\{1,2, \ldots, K\}$ 是总共K个分片的分片ID集合， $\mathcal{M}=\left\{M_1, M_2, \ldots, M_K\right\}$ 是对于所有分片的内存约束。

分片计划 $\pi$ 被表示为从每一个表到一个对应的分片的映射。然每一个设备将获得自己的分片进行处理，令每个分片实际使用的内存表示为 $\hat{\mathcal{M}}=\left\{\hat{M}_1, \hat{M}_2, \ldots, \hat{M}_K\right\}$ （每一个分片中所有表的大小的总和）

$C=\left\{C_1, C_2, \ldots C_K\right\}$ 表示每一个分片操作的执行时间开销

embedding表分片的目的是优化分片计划 $\pi$ 以便于最小化跨分片的最大开销，通过下面公式所表示的内存约束：

$\min _\pi \max (C):=\max _k C_k \quad \text { s.t. } \quad \hat{M}_k \leq M_k, \forall k \in \mathcal{D} .$

方法

micro-benchmark：测量embedding操作的真实开销
1. 初始化：使用embedding表特定的参数去初始化操作，并加载索引数据
2. warmup：多运行几次embedding操作，使得cuda完成对操作的准备
3. benchmarking：多次运行embedding操作，返回平均延迟
cost model: 近似基于从micro-benchmark收集到的数据的多表开销
1. 问题：micro-benchmark需要运行操作才能准确和有效地获得延迟，这对生产环境是非常昂贵的。
2. 方案：使用一个神经开销模型，将开销评估任务转化为一个回归任务，其输入是多表的特征，输出是延迟
3. 使用的特征包括
  1. 表的维度：每一个embedding向量在表中的维度，要标准化成均值是0标准差是1的形式
  2. 哈希大小：表中行的数量。要标准化
  3. 池化因子：用总数量的指数除以批次的大小得到，要标准化
  4. 表的大小：计算参数的大小，不需要标准化
  5. 指数分布：分成17个区间(0~1,1~2,2~4,4~8,8~16以指数的方式递增，直到够17个)，然后统计每个索引在区间索引中出现的次数，并将计数放置到相应的区间中
  6. 步骤感知特征：已经分配的表的比例
4. 定义：令 $(\mathbf{X},\mathbf{y})$ 为收集的数据
  1. $\mathbf{X}$ 是表的特征，其中每一行表示多表的特征，具有可变的长度、
  2. $\mathbf{y}$ 表示通过在GPU上运行micro-benchmark收集到的真实开销的向量
5. 训练：令开销模型为 $f$ ，使用均方差作为损失函数： $L_{cost} = (y-f(\mathbf{X}))^2$
environment：像马尔科夫决策过程的一个分片过程，其通过在每一步中分配一个表
1. 为什么要把分片问题看做一个MDP问题？
  1. 如果直接当做黑盒优化问题处理，需要采样并验证每一个分片计划，这将产生搜索空间过大的问题
  2. 为了解决这个问题，MDP可以分解成多步分片问题，在MDP确定好一个分片计划后，可以直接验证其有效性，并直接引导MDP的agent进行优化
  3. 通过MDP的解决方案，不但可以有效地减少搜素空间（假设有K张表，就只用迭代K次，有M个分片，在每次迭代就只用在M上做决策），同时还能隐含地激励可转移的策略（通过最终的reward引导agent的优化）
2. MDP过程：
  1. State：即将到来的表的特征和一个步骤感知特征
  2. Action：假设有K个分片，Action就是这K个分片的其中一个分片的ID
  3. Reward：在所有的中间迭代中reward为0，最后一个reward表示分片计划的质量
  4. 在每一个表都分片完成之后，需要判断分片几乎是否满足内存约束，如果满足就运行micro-benchmark去获取所有分片的分片延迟 $C$ 。
  5. reward的计算方式为 $\frac{min(C)}{max(C)}$ ，这样可以激励agent在跨分片开销上的平衡，其范围为 $[0,1]$
  6. 如果超出了内存限制，就使用 $((\hat{\mathcal{M}}_k-\mathcal{M}_k)/\mathcal{M}_k)$ 对agent进行惩罚
RL policy：通过试错的方式更新分片策略

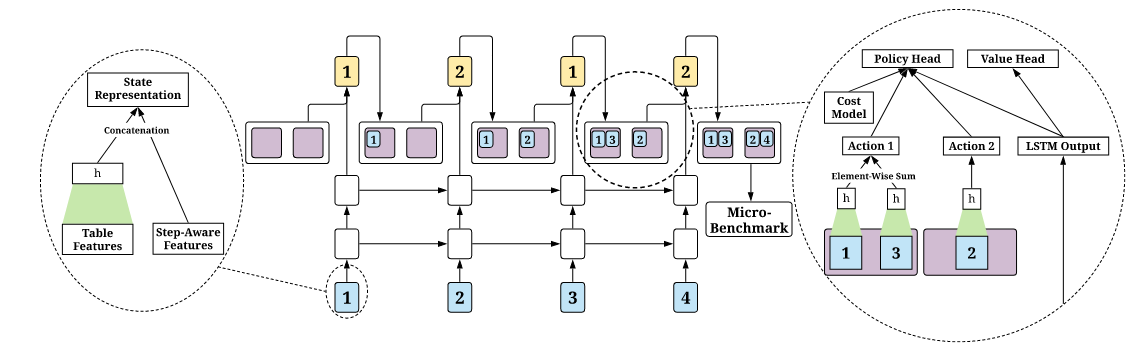
这是policy神经网络的基本结构，模型使用状态特征和动作特征作为输入，输出一个动作可能性向量，每一个可能性的对应坐标就是分片的ID（policy head），同时还输出一个常量值，表示状态的值(value head)

使用一个两成的LSTM去处理state和action
1. 如左边虚线框所示，将表特征和步骤感知特征拼接在一起作为状态表示
2. 然后将状态表示以序列的形式输入到LSTM中
3. 如右边虚线框所示，通过cost model得到的多表表示将和从cost model中得到的predict costs拼接，以构建动作表示
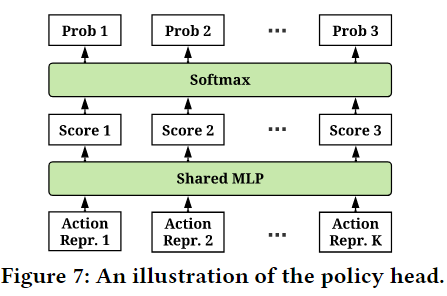
4. 每个动作表示都讲与状态表示连接起来，然后使用MLP，以产生动作的置信度分数，如下图
5. 所有动作分数将由softmax处理，以获得概率向量
令 $s_t,a_t,r_t$ 分别为在第t步的state, action, reward。对于第n步的轨迹 $\left(s_t, a_t, r_t\right)_{t=t^{\prime}}^{t=t^{\prime}+n}$ ，对于 $s_{t^{\prime}}$ 的V-trace的目标b被定义为：

$V_{\text {target }}\left(s_{t^{\prime}}\right)=V\left(s_{t^{\prime}}\right)+\sum_{t=t^{\prime}}^{t^{\prime}+n-1} \gamma^{t-t^{\prime}}\left(\pi_{i=t^{\prime}}^{t-1} c_i\right) \delta_t V,$

其中 $V\left(s_{t^{\prime}}\right)$ 是 $s_{t^{\prime}}$ 的value head的输出， $\delta_t V=\rho_t\left(r_t+\right.\left.\gamma V\left(s_{t+1}\right)-V\left(x_t\right)\right)$ 是时间差。 $c_i$ and $\rho_t$ 用于处理模型延迟更新的截断重要性采样权重。然后第t步的损失可以定义为

$L_t=\rho_t \log \pi\left(a_t \mid s_t\right)\left(r_t+\gamma V_{\text {target }}\left(s_{t+1}-V\left(s_t\right)\right)+\frac{1}{2}\left(v_t-V\left(s_t\right)\right)^2,\right.$

其中 $\pi\left(a_t \mid s_t\right)$ 和 $V\left(s_t\right)$ 分别为policy head和value head。

算法 1：AutoShard训练

输入：训练任务 $\mathcal{S}_{train}=\{\mathcal{S_i}\}_{i=1}^n$ ，policy-value网络的bs $B_1$ ，cost model的bs $B_2$ ，cost model迭代更新的次数 $I$ ，数据收集步骤的数值 $T$

初始化cost model和poliocy-value网络

for iteration=1,2,… until 收敛 do

从 $\mathcal{S}_{train}$ 的任务中随机采样 $T$ 步，并收集其轨迹集合 $\{s_t,a_t,r_t\}_{t=1}^T$ 并存储和生成开销数据到buffer中

if 收集了超过 $B_1$ 的轨迹集合 then

按照上面 $L_t$ 的公式更新policy-value网络

for iteration=1,2,…, $I$ do

从buffer中采样大小为 $B_2$ 的开销数据的batch，并使用MSE Loss更新cost model

end for

end if

end for