简要

在推荐系统中大部分的方法为所有的特征固定了embedding的纬度，这可能会收到以下影响：

  1. embedding可能包含数百亿个参数，导致高内存使用和计算成本
  2. 过度参数化低频特征可能导致过拟合，甚至产生意外噪声

此外，高频特征需要更多的参数来传递有效的信息。

提出单次嵌入维度搜索方法（SSEDS），能够通过使用单次embedding剪枝操作有效的分配每个特征域对应的维度同时保持模型的推荐准确率。

如何自动地为不同的特征分配embedding维度是很重要的问题，本文称为embedding维度搜索（EDS）问题。

这个问题需要解决两个挑战

  1. 如何识别各个特征域的embedding维度
    1. 识别embedding每个维度的重要性，然后去除不重要的相关维度，以实现自动获取混合维度embedding
    2. 标记每个特征域的embedding维度，同时保持其他的不变。然后通过评估他对损失函数的影响，计算每个维度的显著分数，以此表达维度的重要性。
  2. 如何通过一种有效的方式搜索embedding维度
    1. 通过观察显著分数，可以对所有特征域的embnedding维度进行降序排列，并根据给定的参数预算保留有限的部分。
  3. 如何聚合SSEDS到传统的推荐模型中
    1. 首先以标准的方式对传统模型进行预训练，然后通过使用single-shot embedding pruning获得具有混合维度embedding的超薄模型，接着使用预训练和混合embedding初始化和重新训练slim模型，并为每个特征字段引入额外的变换矩阵来对齐维度，以便进一步的特征交互操作。

贡献点：

  1. 提出有效的单词嵌入搜索方法SSEDS，引入了一个通过一次前向-反向传播就能识别每个特征域的每个embedding维度的重要性。

  2. SSDES是模型不可知的，提出利用线性变换矩阵来对齐不同特征域的维度，使其能够无缝集成到各种基本的推荐模型中。还能灵活地控制袖箭参数的数量，以满足不同的参数预算要求。

方法

问题描述

基于特征的推荐系统的典型训练数据D\mathcal{D}通常由用户点击记录构成，每个点击记录(x,y)∈D(\mathrm{x}, y) \in \mathcal{D}的表示为：

(x,y)=({x1,x2,…,xm},y)(\mathrm{x}, y)=\left(\left\{\mathrm{x}_1, \mathrm{x}_2, \ldots, \mathrm{x}_m\right\}, y\right)

其中x={x1,x2,…,xm}\mathrm{x}=\left\{\mathrm{x}_1, \mathrm{x}_2, \ldots, \mathrm{x}_m\right\}表示原始特征向量，由于用户和物品相关的m个特征域拼接而成。y\mathcal{y}是一个二元标签(1表示点击，0表示不点击)，描述了用户对给定物品的喜好。对于每个特征域，他通常包含一个确定数量的独一无二的特征，因此第i个域的特征向量xi∈x\mathrm{x}_i \in \mathrm{x}通常被编码为高维稀疏one-hot或者multi-hot的向量。为了进一步提取用户的喜好，大部分现代基于特征的推荐系统将xi∈Rni\mathrm{x}_i \in \mathbb{R}^{n_i}（nin_i是在第i个域的独一无二的特征的数量）映射到低维密集空间ei=Vixi\mathbf{e}_i=\mathrm{V}_i \mathrm{x}_i中。其中Vi∈Rd×ni\mathrm{V}_i \in \mathbb{R}^{d \times n_i}第i个特征域的embedding表，dd是共享在所有域的embedding维度。整个embedding表V={V1,V2,..,Vm}V=\{V_1,V_2,..,V_m\}可以通过链接每个域的所有嵌入表来获得。

因此，基于特征的推荐系统ff的目标是预测用户是否会点击这个物品的概率pp

p=f(x∣V,Θ)p=f(\mathrm{x} \mid \mathrm{V}, \Theta)

其中Θ\Theta表示模型的其他参数

最后，为了得到混合维度embedding，基于EDS方法的embedding剪枝的目标是根据parameter budge κ∈(0,1]\kappa \in(0,1]，从整个embedding表中识别和去除一定数量的embedding维度，同时最小化损失函数

V∗,Θ∗=arg⁡min⁡V,ΘL(V,Θ;D), s.t. ∥V∗∥0<κ∥V∥0\mathrm{V}^*, \Theta^*=\underset{\mathrm{V}, \Theta}{\arg \min } \mathcal{L}(\mathrm{V}, \Theta ; \mathcal{D}), \text { s.t. }\left\|\mathrm{V}^*\right\|_0<\kappa\|\mathrm{V}\|_0

其中L\mathcal{L}是损失函数，∥⋅∥0\|\cdot\|_0表示L0L_0范数，最终优化剪枝的嵌入表所期望的非零参数V∗\mathrm{V}^*。

SSEDS

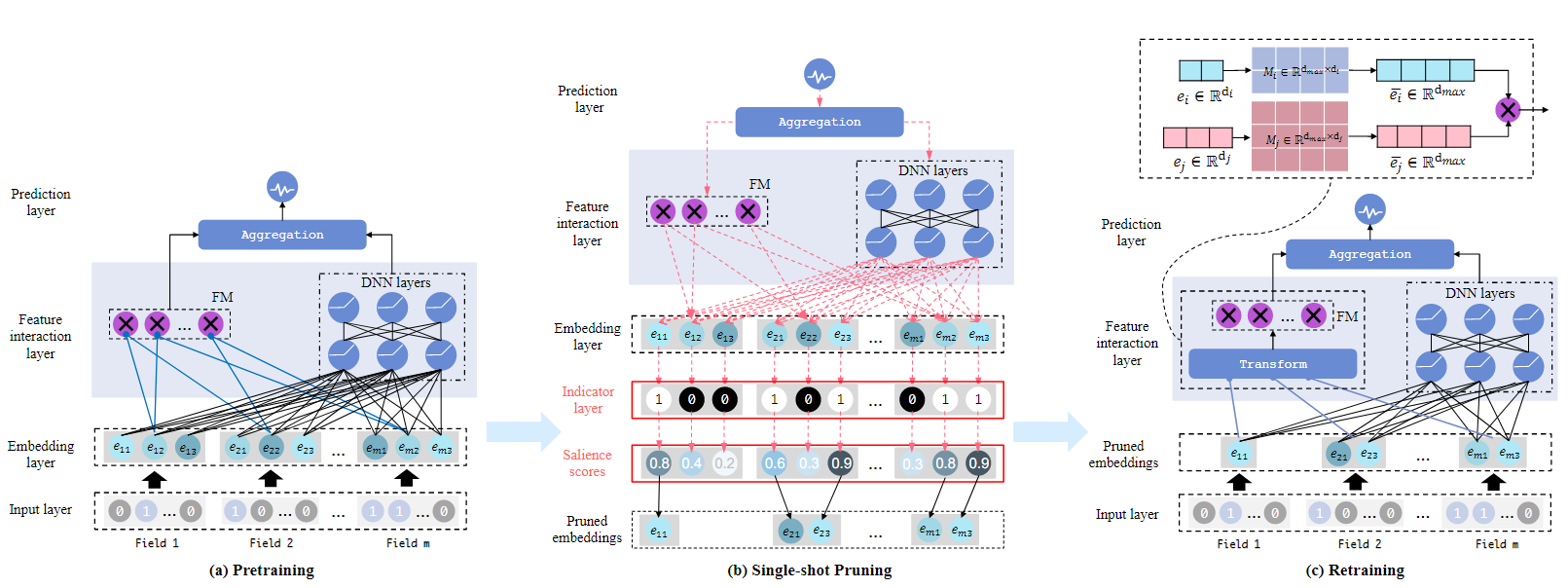
image-20230220094308779

SSEDS有三个阶段，Pretraining，Single-shot Pruning，Retraining。在Pretraining阶段是使用标准的方式训练统一维度的推荐模型，通过标准的方法的over-parameterized embedding会更加具有表达性。在Single-shot Pruning阶段会首先计算每个embedding维度的显著份额数，然后降序排序，然后以序列的方式去除维度，直至到达预先定义的参数预算，从而获得混合维度的embedding。最后的Retraining阶段，由于传统模型在特征交互层中需要相同的维度，因此在直接使用混合维度的embedding之前，需要使用转化矩阵，将混合维度的embedding与特征交互层的参数进行对齐，然后再进行训练。通过这样的方式，混合维度embedding能够轻易地聚合到出传统模型的结构上。

Pretraining

对于每一个训练实例，嵌入层使用原始特征x={x1,x2,...,xm}x=\{x_1,x_2,...,x_m\}作为输入，并将其通过公式1：ei=Vixie_i=V_ix_i映射到embedding e={e1,e2,...,em}e=\{e_1,e_2,...,e_m\}中。然后使用特征交互层的特征交互操作g(⋅)g(\cdot)去捕获这些embedding VV中的隐式交互关系:

公式2：z=g( V,Θ)公式2：\mathrm{z}=g(\mathrm{~V}, \Theta)

当zz作为要输入到最后的预测层的特征，其得到预测可能性pp的过程如下公式所示：

公式3：p=sigmoid⁡(z)公式3：p=\operatorname{sigmoid}(\mathrm{z})

在embedding层和特征交互层的可学习参数分别为VV和Θ\Theta。损失函数L(V,Θ;D)\mathcal{L}(V,\Theta;\mathcal{D})用于测量模型预测可能性pp和ground-truth标签yy的差异，通过下面的公式

公式4：L(V,Θ;D)=−∑{x,y}∈D{y⋅log⁡(p)+(1−y)⋅log⁡(1−p)}公式4：\mathcal{L}(V, \Theta ; \mathcal{D})=-\sum_{\{\mathrm{x}, y\} \in \mathcal{D}}\{y \cdot \log (p)+(1-y) \cdot \log (1-p)\}

通过最小化损失L(V,Θ;D)\mathcal{L}(V,\Theta;\mathcal{D})，可以得到最优的在所有特征域上具有统一embedding维度dd的embedding表 V^\hat{\mathrm{V}} ，以及其他的参数Θ^\hat{\Theta}。

Single-shot Pruning

在这里引入了一个显著性标注去区分每一个域i∈{1,...,m}i\in\{1,...,m\}以及每一个维度j∈{1,...,d}j\in\{1,...,d\}中的每一个 V^ij\hat{\mathrm{V}}_{ij}的embedding维度的重要性。引入了一个二元参数的辅助指标层α={α1,α2,...,αm},αi∈[0,1]d×ni\alpha=\{\alpha_1,\alpha_2,...,\alpha_m\},\alpha_i\in[0,1]^{d\times n_i}。然后对于期望的参数开销κ\kappa，可以重新定义目标函数为：

公式5：min⁡V^,Θ^,L(V^⊙α,Θ^;D) s.t. α∈{0,1}d×∑imni,∥α∥0<κ∥V∥0公式5：\begin{array}{l} \min _{\hat{\mathbf{V}}, \hat{\Theta}}, \mathcal{L}(\hat{\mathbf{V}} \odot \alpha, \hat{\Theta} ; \mathcal{D}) \\ \text { s.t. } \alpha \in\{0,1\}^{d \times \sum_i^m n_i},\|\alpha\|_0<\kappa\|\mathrm{V}\|_0 \\ \end{array}

其中⊙\odot表示Hadamard乘积。α\alpha和V^\hat{V}有相同的大小，然而本文不尝试直接最优化公式5，而是利用α\alpha去决定每个embedding维度的重要性。具体来说，本文会通过标记他同时保持其他维度不改变embedding值的方式独立地测量第i个域的第j个维度对损失函数的有效性，接着测量loss值的变化

公式6：ΔLi,j=L(V^⊙1,Θ^;D)−L(V^⊙(1−ϵi,j),Θ^;D)公式6：\Delta \mathcal{L}_{i, j}=\mathcal{L}(\hat{\mathbf{V}} \odot 1, \hat{\Theta} ; \mathcal{D})-\mathcal{L}\left(\hat{\mathbf{V}} \odot\left(1-\epsilon_{i, j}\right), \hat{\Theta} ; \mathcal{D}\right)

其中1是一个全为1，维度为 ∑imni×d\sum_i^m n_i \times d的矩阵，指标矩阵ϵi,j∈{0,1}∑imni×d\epsilon_{i, j} \in\{0,1\}^{\sum_i^m n_i \times d}是一个二元向量，其除了在第i个域的第j个维度上，其他地方全为0。然而，计算所有的ΔLi,j\Delta{\mathcal{L}}_{i,j}是非常昂贵的。另一方面L\mathcal{L}对于α\alpha是不可微的。因此简化α\alpha的二元约束到[0,1][0,1]之间，这样在α=1\alpha=1时，ΔLi,j\Delta \mathcal{L}_{i, j}可以近似地用梯度∂L/∂αi,j\partial \mathcal{L} / \partial \alpha_{i, j}（表示为gi,j(V^,Θ^;Db)g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)）表示。

公式7：ΔLi,j≈gi,j(V^,Θ^;Db)=∂L(V^⊙α,Θ^;Db)∂αi,j∣α=1=lim⁡δ→0L(V^⊙α,Θ^;Db)−L(V^⊙(α−δϵi,j),Θ^;Db)δ∣α=1公式7：\begin{aligned} \Delta \mathcal{L}_{i, j} & \approx g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)=\left.\frac{\partial \mathcal{L}\left(\hat{\mathbf{V}} \odot \alpha, \hat{\Theta} ; \mathcal{D}_b\right)}{\partial \alpha_{i, j}}\right|_{\boldsymbol{\alpha}=1} \\ & =\left.\lim _{\delta \rightarrow 0} \frac{\mathcal{L}\left(\hat{\mathbf{V}} \odot \alpha, \hat{\Theta} ; \mathcal{D}_b\right)-\mathcal{L}\left(\hat{\mathbf{V}} \odot\left(\alpha-\delta \epsilon_{i, j}\right), \hat{\Theta} ; \mathcal{D}_b\right)}{\delta}\right|_{\boldsymbol{\alpha}=\mathbf{1}} \end{aligned}

通过这种方式，能够通过只通过一次前向-反向传播，自动地在数据集D\mathcal{D}的mini-batch（表示为Db\mathcal{D}_b）上，有效地计算所有的gi,j(V^,Θ^;Db)g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)。∣gi,j(V^,Θ^;Db)∣\left|g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)\right|的数值比较大意味着相应维度对损失函数的影响更好（积极或消极)，因此应该保留。基于这个假设，第i个域的第j个维度的显著性分数si,js_{i,j}为∣gi,j(V^,Θ^;Db)∣\left|g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)\right|的归一化值。

公式8：si,j=∣gi,j(V^,Θ^;Db)∣∑i=0m∑j=0d∣gi,j(V^,Θ^;Db)∣公式8：\mathrm{s}_{i, j}=\frac{\left|g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)\right|}{\sum_{i=0}^m \sum_{j=0}^d\left|g_{i, j}\left(\hat{\mathbf{V}}, \hat{\Theta} ; \mathcal{D}_b\right)\right|}

在得到所有的显著性分数si,js_{i,j}后，将他们进行降序排列，然后序列化地去除低显著性分数的维度，直至到达参数预算κ\kappa，αi,j\alpha_{i,j}的计算方式如下：

公式9：αi,j=I(si,j−s~≥0),∀i∈{1,…,m},j∈{1,…,d} s.t. ∥α∥0<κ∥V∥0公式9：\begin{array}{c} \boldsymbol{\alpha}_{i, j}=\mathbb{I}\left(\mathrm{s}_{i, j}-\tilde{s} \geq 0\right), \forall i \in\{1, \ldots, m\}, j \in\{1, \ldots, d\} \\ \text { s.t. }\|\boldsymbol{\alpha}\|_0<\kappa\|\mathrm{V}\|_0 \end{array}

其中 I(⋅)\mathbb{I}(\cdot)是指标函数，分位数的值s~\tilde{s}自动地由参数预算决定。

Retraining

在完成剪枝后，混合维度embedding表V‾={V‾1,⋯ ,V‾q}q≤m2,V‾i∈Rdi×ni\overline{\mathrm{V}}=\left\{\overline{\mathrm{V}}_1, \cdots, \overline{\mathrm{V}}_q\right\}_{q \leq m}{ }^2, \overline{\mathrm{V}}_i \in \mathbb{R}^{d_i \times n_i}会被自动地获得，其中did_i是第i个域的搜索空间，q是剪枝后域的数量。然而传统推荐模型，比如FM和DeepFM由于特征交互操作，要求输入的embedding维度一致。为了使剪枝的embedding能够聚合到多个模型结构中，需要对齐embedding维度到不同的域中。本文利用一个简单而有效的方法去对齐维度，具体来说，本文只引入qq个域变换矩阵M={M1,…,Mq},Mi∈Rdmax⁡×di\mathrm{M}=\left\{\mathrm{M}_1, \ldots, \mathrm{M}_q\right\}, \mathrm{M}_i \in \mathbb{R}^{d_{\max } \times d_i}，其中dmax⁡=max⁡(d1,⋯ ,dq)d_{\max }=\max \left(d_1, \cdots, d_q\right)是对齐embedding维度等于所有搜索维度中的最大维度。本文可以得到对于特征xi\mathrm{x}_i对齐后的embedding e‾i∈Rdmax⁡\overline{\mathrm{e}}_i \in \mathbb{R}^{d_{\max }}。

公式10：e‾i=MiV‾ixi公式10：\overline{\mathrm{e}}_i=\mathrm{M}_i \overline{\mathrm{V}}_i \mathrm{x}_i

值得注意的是，我们只引入了一小部分的额外参数。此外，MiM_i能够提高剪枝embedding Vˉ\bar{V}的表示能力

  1. 他们被映射到具有更多视角用于表达的更高维度空间
  2. MiM_i在ii域中的所有特征实例中共享。

因此他们共同的特征被进一步建模。在对其之后传统推荐模型在第i个域和第j个域之间的点积操作<⋅><\cdot>能够被执行

公式11：<e‾i,e‾j>公式11：<\overline{\mathrm{e}}_i, \overline{\mathrm{e}}_j>

此外点积操作，剪枝的embedding也容易适应到其他特征交互操作中。比如，DNN层只需要去适应输入层的维度，以匹配embedding层输出的维度。

在对其之后，需要重新训练embedding表Vˉ\bar{V}，转换矩阵MM，最终轻量模型的其他模型参数 Θˉ\bar{\Theta} 。

伪代码

算法1：SSEDS算法

要求：训练数据D\mathcal{D}，基本模型f(V,Θ)f(V,\Theta)，参数预算κ\kappa，损失函数L\mathcal{L}

确保：混合维度embedding表V∗V^*使得∣∣V∗∣∣0<κ∣∣V∣∣0||V^*||_0 < \kappa||V||_0

  1. Pretraining:
    1. 优化VV和Θ\Theta: V^,Θ^←fV\hat{\mathrm{V}}, \hat{\Theta} \stackrel{f}{\leftarrow} \mathrm{V}，Θ\Theta属于基本模型ff
  2. Single-shot Pruning
    1. 采样一个mini-batch的数据集Db∼D\mathcal{D}_b\sim\mathcal{D}
    2. 识别第i个域的第j个维度的显著性分数sijs_{ij}（公式8）
    3. 降序排序sijs_{ij}
    4. 剪枝embedding表Vˉ←V^\bar{V}\leftarrow\hat{V}(公式9)
  3. Retraining
    1. 对齐embedding维度（公式10）
    2. 重训练轻量模型V∗,Θ∗←V^,Θ^V^*,\Theta^*\leftarrow\hat{V},\hat{\Theta}